Лабораторная работа по математике на тему: "Вывод формулы длины окружности и площади круга"

• Обучающие. Опытным путем получить зависимость между длиной окружности и её диаметром, вывести формулы длины окружности и площади круга.
• Развивающие. Способствовать дальнейшему развитию внимания, наблюдательности, самоконтроля учащихся.
• Воспитательные. Воспитывать аккуратность и дисциплинированность школьников, умение работать в тишине, помогать товарищам.

Оборудование

Учащиеся должны иметь с собой картон, лист цветной бумаги, ножницы, нитки, циркуль, цветной карандаш, простой карандаш, клей-карандаш, калькулятор, линейку, фломастер.

В первую очередь актуализируются опорные знания, необходимые для выполнения лабораторной работы. Учащимся предлагается ответить на следующие вопросы:

1. Что называют отношением двух величин?
2. Как округлить десятичную дробь до десятых? До сотых?
3. Чему равна площадь прямоугольника?
4. Что такое окружность? Радиус? Диаметр?
5. Если фигуру площадью S разделить на части с площадями S1 и S2, будет ли выполняться равенство S=S1+S2
6. Если фигуру площадью S разделить на части и из них составить другую фигуру, будет ли её площадь равна площади первоначальной фигуры?

Второй этап.

Учащиеся выполняют практические задания по команде учителя и записывают свои наблюдения (учитель может все проделывать на доске, если класс не достаточно подготовлен к самостоятельной работе, или предложить ученикам работать в парах).

1. На картонном листе начертить окружность с произвольным радиусом, отметить её центр, записать значение радиуса в миллиметрах(R) и значение диаметра в миллиметрах(D).
2. Провести клеем-карандашом по окружности и, пока клей не высох, проложить нитку точно по контуру окружности и аккуратно отрезать её на стыке.
3. Снять нитку с картона и очень точно измерить её длину в миллиметрах. Этот размер назовем длиной окружности(L). Записать значение L.
4. Найти отношение

с помощью калькулятора, округлить получившуюся дробь до тысячных, до сотых, до десятых, до целых. Сделать соответственные записи.

Далее ученики называют свои результаты и замечают, что, хотя окружности были построены у всех разные, отношения длины к диаметру получились примерно одинаковые.

Историческая справка.

Отношение длины окружности к её диаметру – величина постоянная и не зависит от размеров окружности. Число, выражающее это отношение, принято называть греческой буквой (“пи”) – первой буквой слова “периферия” (греч. “окружность”). Общеупотребительным такое обозначение стало с середины восемнадцатого века. Число выражается бесконечной непериодической десятичной дробью и приближенно равно 3,141592653589…

В глубокой древности считалось, что окружность ровно в 3 раза длиннее диаметра. Эти сведения содержатся в клинописных табличках Древнего Междуречья. Итак, первым приближением числа было 3. Однако уже во II тысячелетии до н.э. математики Древнего Египта находили более точное отношение.

Три первые цифры числа =3,14…запомнить совсем несложно. А для запоминания большего числа знаков существуют забавные поговорки и стихи. Например, такие:

Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.

С.Бобров. “Волшебный двурог”

Четвертый этап.

Вывод формулы длины окружности.

Итак, мы имеем следующее соотношение: =. Выведем из этой формулы L: L=D или L=2R. Эта формула называется формулой длины окружности. Чтобы найти длину окружности, надо знать её радиус или диаметр.

Учащимся предлагается выполнить несколько упражнений:

1. D=6см, найти L.
2. R=3дм3мм, найти L.
3. L=6см, найти R.
4. L=8мм, найти R.

Пятый этап.

Вывод формулы площади круга.

Учащиеся выполняют практические задания по команде учителя (учитель может проделывать все на доске).

1. На листе цветной бумаги начертить окружность с произвольным радиусом и провести фломастером по её контуру.
2. Разделить круг с помощью линейки и карандаша на несколько секторов, затем разрезать его. (см. рис.1) Заметим, что не следует делить круг на меньшее, чем 8 секторов.

3. В одном из секторов следует провести радиус, делящий его на 2 равных сектора, которые назовём крайними (см. рис.2) и отложить.

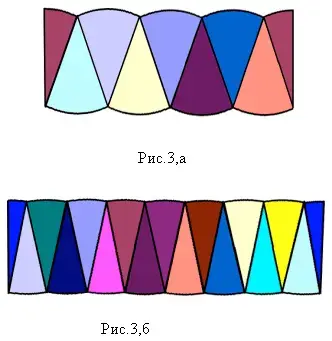
4. На картонном листе провести горизонтальную прямую и приклеить вдоль неё сектора, как показано на рис.3. (На рис.3,а – круг разделен на 8 секторов, на рис.3,б – на 16 секторов). Крайние сектора приклеить по краям. Заметно, что получившаяся фигура при увеличении количества секторов становится очень похожей на прямоугольник. Значит, и её площадь можно найти по формуле площади прямоугольника. Ширина нашего прямоугольника равна радиусу окружности(R), а длина прямоугольника равна половине длины окружности (). Площадь прямоугольника равна произведению длины на ширину, т. е. S=, а т.к. L=2R, значит S= или S=R².

.Так как прямоугольник был составлен из частей круга, то их площади равны. Значит, площадь круга равна: S=R.

Шестой этап.

Применение формул для решения задач.

1. Сравнить площади кругов с радиусами 3дм и 300мм.
2. Найти площадь круга, если D=6см.
3. Найти площадь круга, если L=10.
4. Сравнить площадь круга с R=5см с площадью квадрата со стороной 5см.

Седьмой этап.

Этап контроля.

Следует отметить, что этот этап нужно включать в ход урока, если использован двухчасовой урок. В этом случае можно провести небольшую проверочную работу, которую учащиеся выполнят прямо на своих картонных листах. Учитель оценит правильность решения задач и аккуратность выполнения практической части.

В противном случае оценивается только практическая часть.

Комментарий: Данный урок является нетрадиционным, что особенно нравится детям любого возраста. Практика показывает, что получение или вывод формул “своими силами” прочно запоминается ввиду своей наглядности, четко простроенной цепочки выводов. Для учащихся 5-6 классов формулы длины окружности и площади круга – одни из первых, которые надо прочно запомнить. Так пусть дети их выведут сами!