Нетрадиционный развивающий метод преподавания планиметрии по методике Г.К. Муравина
Геометрия как наука и геометрия как учебная дисциплина представляют собой, пожалуй, самый удивительный феномен человеческой культуры. Возникая на основе естественного созерцания окружающих пространственных форм и столь же естественных потребностей человеческой практики, геометрия превратилась в огромное многоэтажное здание, каждый этаж которого был не только великолепным архитектурным произведением сам по себе, но и служил фундаментом других, не менее великолепных зданий. А сколько фундаментальных физических теорий уходит корнями в геометрические недра! Несмотря на заявления некоторых крупных математиков о том, что геометрия как наука утратила свое значение и превратилась только в удобный и привычный язык математики, действительность убеждает нас в обратном. По-прежнему ведутся успешные и интересные исследования в самой геометрии, полученный геометрический опыт реализуется в практической деятельности человека. Геометрия является одним из основных средств формирования концептуальных представлений об окружающем реальном пространстве. Неудивительно, что становление и развитие геометрической мысли служит постоянной опорой в философской теории познания.
Педагогическое же значение геометрии как базового учебного предмета является вообще бесценным. Геометрия является элементом общей человеческой культуры, а целенаправленное ее изучение формирует и развивает не только математические, но и общеинтеллектуальные способности. Уникальность геометрии как учебного предмета заключается в том, что она позволяет наиболее ярко наблюдать, формировать и развивать мыслительные процессы различных видов и уровней. Успешное изучение геометрии невозможно без развитого наглядного и абстрактно - теоретического мышления. Геометрический материал предоставляет прекрасные возможности для цельного и гармоничного развития интуитивного, логического, пространственного, символического и конструктивного компонентов умственной деятельности. Кроме того, пожалуй, нет ни одного другого учебного предмета, где ведущие компоненты (знания, способы деятельности) были бы так взаимосвязаны. Заметим, что большое число исследований в педагогической психологии выполнено на базе обучения геометрии. Относительная простота и убедительная наглядность сходных геометрических абстракций позволяет гораздо раньше, чем в других учебных предметам, формировать их, и при изложении использовать дедуктивный метод. Геометрические знания обеспечивают многочисленные внутриматематические связи и связи математики с другими предметами. Геометрия имеет широкие возможности для формирования эмоционально-мотивационной сферы обучения и для эстетического развития учащихся. Поэтому вряд ли можно серьезно говорить о всестороннем развитии ребенка без специального его обучения геометрии.
Содержание школьного курса геометрии и методика его преподавания - извечный предмет незатихающих и подчас бурных споров.
В качестве реального факта и исходной позиции для дальнейших рассуждений необходимо признать, что достаточно большая часть школьной молодежи отличается объективным неприятием математики (особенно более абстрактных и логических ее аспектов).
Здесь нет ничего неестественного, неожиданного или ужасного существуют же (почти в каждом классе!) дети с отсутствием музыкального слуха, с нерасположенностью к иностранным языкам и т.д. Это отнюдь не дети с ограниченными интеллектуальными возможностями - просто таковы их личностные особенности и специфика психики, просто способности многих из них реализуются в какой-то иной сфере, которую необходимо кропотливо искать, не заставляя насильно делать неинтересное.
Но учить всех предметам учебного плана необходимо. Каков выход? Сделать объяснение понятным, наглядным, доступным, а значит и интересным. При правильном использовании методики Георгия Константиновича Муравина ученики самостоятельно работают с новым материалом с самого начала практически без ошибок. Основой программы по геометрии в 7 классе являются теоремы о признаках равенства треугольников. Перед разговором о признаках равенства треугольников 2 урока посвящены теме: "Построение треугольников". Вот примерное планирование урока:
1.Устные упражнения.
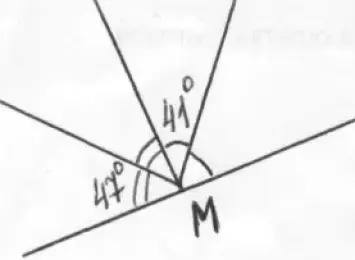
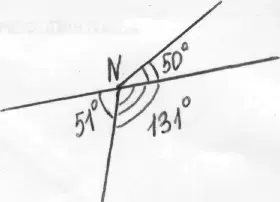
Развернутый угол разделен лучами на три угла. Второй угол больше первого на 100, а третий больше второго на 200 .
А) Найдите величины углов, на которые разделился развернутый угол.
Б) Найдите угол, образованный биссектрисами меньшего и большего из этих углов.
В) Есть ли на рисунке смежные углы с вершинами в точках М или N.
2. Упражнения на глазомер. В левой части доски учитель изображает треугольник.
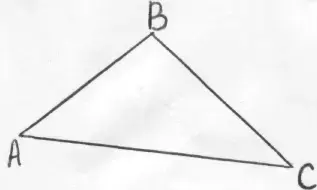
К доске вызывается доброволец, чтобы изобразить копию этого треугольника правой части доски. В это время ученики на местах рисуют в своих тетрадях треугольники и предлагают своим соседям по парте скопировать их на глаз. Как проверить, получился ли такой же треугольник? (сравнить длины сторон с помощью циркуля). После проверки доказавшей, что стороны треугольников не равны, правый треугольник стирается.
3. Попробуем построить такой же треугольник, используя циркуль и линейку. Обозначим вершины треугольника буквами А,В,С. Вершины треугольника, который мы будем строить, обозначим теми же буквами с индексами: А1, В1, С1.
1) Построим сначала А1С1=АС. Для этого проведем какую-нибудь прямую, отметим на ней точку А1, измерим сторону АС, и отложим от А1 отрезок ей равный. Так получаем вторую вершину треугольника точку С1.
2) Точка В1 должна находится от точки А1 на расстоянии равном длине стороны АВ треугольника ABC, то есть точка В1 должна лежать на окружности с центром в точке А1 и радиусом равным АВ.
3) Конечно, этого еще недостаточно, чтобы определить положение точки В1, но мы знаем, что она должна стоять от точки С1 на таком же расстоянии, как вершина В от вершины С. Другими словами, точка В1 должна лежать на окружности с центром в точке С1 и радиусом, равным СВ. Две эти окружности имеют две точки пересечения В1 и В2. Оказывается, мы можем построить даже два треугольника (лишний треугольник стирается). Наверное, нужно было сразу договориться, в какой из полуплоскостей по отношению к прямой А1С1 мы будем строить треугольник. Ясно, что стороны треугольников ABC и А1В1С1 равны, а как у них с углами? (Равны). Неудивительно, ведь в верхней полуплоскости есть единственная точка В1. Для любой другой точки были бы другие длины сторон треугольника.
5) Самостоятельная работа в парах. Построить треугольник со сторонами: 3см, 4см и 5см.
Как проверить, равны ли ваши треугольники (наложить листки бумаги и посмотреть на просвет).
Оцените величины углов и проверьте свои результаты с помощью транспортира.
6. Задание на дом.
- Тренировка в построении, оценке.
- Построить треугольник со сторонами 2 см, 4 см и 5 см.
- Вырезать из бумаги какой-нибудь треугольник, измерить его стороны и углы. Обязательно принести его на следующий урок.
Затем сам урок "Признаки равенства треугольников". Сразу делается вывод трех признаков равенства треугольников. Такова методика изучения определений, формулировок теорем. И действует здесь методика Г.К. Муравина на 100%. А вот научить детей безошибочно доказывать любые теоремы, решать любые задачи невозможно. Решение задач и доказательство теоремы - творческий процесс. Ему можно и необходимо учить, но невозможно научить.
Чему же следует в соответствии с методикой Муравина, учить, отыскивая решения задач и доказательства теорем?
Первое - у Г.К. Муравина теорем, как предложений, требующих, доказательство, нет. По его методике в геометрии решаются три вида задач - задачи на построение, задачи на доказательство (теоремы), задачи на вычисления.
Наблюдение за процессом обучения решению задач показывает, что чаще всего используется универсальный, но, к сожалению, варварский способ.
Чтобы научить плавать, бросают в воду: "если не потонет, то научится..." При этом помощь учителя "тонущему" ученику нередко заключается в призывах подумать.
Беда состоит в том, что просто "думать" никто не умеет, люди думают лишь над чем-то. Попытаемся разобраться над чем именно должен думать ученик, отыскивая решения, как научить "умению видеть", "умению думать".
1. Упражнения на глазомер. Провести окружность, проходящую через заданные точки от руки, построить угол, равный данному, оценить величину угла, сравнить длины отрезков на глаз и т.д.
2. На прошлом уроке мы познакомились с тремя условиями, наличие которых позволяет сделать вывод о равенстве треугольников. Сегодня учимся определять, есть ли на рисунке равные треугольники. Нам надо находить или по две равные стороны и угол между ними, или по стороне с двумя прилежащими к ней углами, или по трем сторонам.
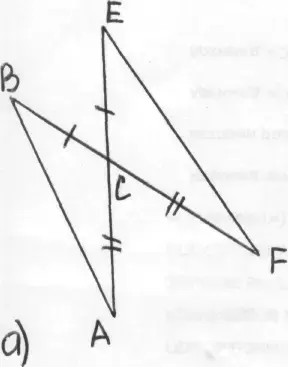
По рисункам могут быть поставлены следующие вопросы:
- Есть ли на рисунке равные отрезки?
- Есть ли на рисунке равные углы?
- Какие равные элементы имеют изображенные треугольники?
- Можно ли сделать вывод о равенстве треугольников?
- Что можно сказать об отрезках АБ и ЕF?
- Что можно сказать об углах этих треугольников?
- Как записать равенство треугольников. чтобы по записи было бы легко назвать равные элементы?
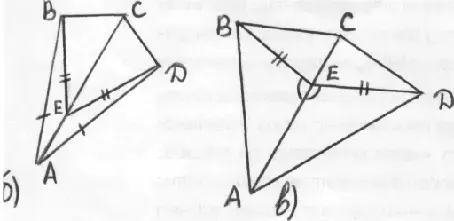
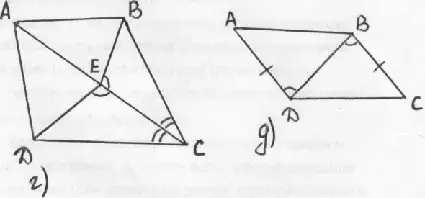
б) - д) - Работа аналогична:
Итак, обнаружив, что углы между равными сторонами в треугольниках соответственно равны, мы сделали вывод о равенстве треугольников и получили, кроме того, равенство отрезков АВ и ЕF. Равенство каких еще элементов мы можем отметить?
Укажите все пары равных треугольников и объясните, как вы пришли к выводу об их равенстве. Например: в) ? ABE = ![]() АДЕ (по двум сторонам и
углу между ними), следовательно, < ВАЕ=< ДАЕ и АВ=ДА.
АДЕ (по двум сторонам и
углу между ними), следовательно, < ВАЕ=< ДАЕ и АВ=ДА. ![]() ABC=
ABC= ![]() АДС (по двум сторонам и углу между ними), следовательно, ВС=ДС.
АДС (по двум сторонам и углу между ними), следовательно, ВС=ДС. ![]() ВЕС=
ВЕС= ![]() ДЕС
(по трем сторонам).
ДЕС
(по трем сторонам).
ПРИМЕЧАНИЕ: проявляющиеся в процессе решения равенства элементов отмечаются другим цветом.
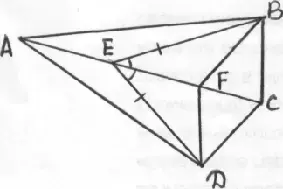
3. Групповая работа (создаются группы-бригады по 4-6 школьников).
Исследовать конфигурацию: отметить равные отрезки и углы, выписать пары равных треугольников со ссылками.
4. Задание на дом. В конфигурации найти и выписать как можно больше равенств.
Затем цепочка - творческого осмысления задач продолжаете при работе по индивидуальным карточкам и при работе с печатными тетрадями.
Теперь остановимся на простой задаче из курса 8 класса и сосредоточим усилия не на ее решении, а на подходах к его отысканию.
Дан параллелограмм АВСД. На его противоположных сторонах АВ и СД от противоположных вершин А и С отложены равные между собой отрезки АМ и СN. Доказать, что четырехугольник МВNД - параллелограмм.
Из определения параллелограмма следует, что у рассматриваемого в задаче четырехугольника противоположные стороны попарно параллельны ВС||АД. Кроме того, если ученикам уже известны теоремы о диагоналях параллелограмма и о равенстве его противоположных сторон и углов, то из условия можно сделать следующие выводы:
(АВСД - параллелограмм);
(диагонали АС и ВД, пересекаясь, делятся пополам);
(параллелограмм); (АВ = СД и ВС = АД),
(равны противоположные углы А и С, В и Д).
Продолжим поиск решения. Возникает вопрос, каким именно из множества выводов, которые можно сделать, рассмотрев условие, следует воспользоваться. Чтобы ответить на этот вопрос, рассмотрим заключение теоремы и сделаем выводы, приближающие нас к заключению. Прежде всего внимательно прочитаем то, что требуется сделать. В рассматриваемой задаче надо доказать, что MBNД - параллелограмм. Остается понять, каким образом это можно установить.
Попробуем воспользоваться определением, которое всегда предназначено для того, чтобы решить вопрос можно или нельзя обозначить объект нужным термином. В данном случае достаточно установить параллельность сторон ВN и МД, ВМ и NД. Остается доказать, что эти прямые действительно параллельны.
Внимание! О параллельности ВN и МД известно из определения параллелограмма АВСД (ВN - та же самая прямая, что и ВС, МД - та же самая прямая, что и АД).
Значит, для отыскания решения надо только понять, каким образом можно установить параллельность ВМ и МД.
Подумаем, нельзя ли воспользоваться одним из известных ученикам признаков параллельности двух прямых:
- если две прямые перпендикулярны одной и той же прямой, то они параллельны;
- две прямые параллельные одной и той же прямой, параллельны между собой;
- если две прямые пересечены третьей и образовавшейся при этом накрест лежащие углы равны, то прямые параллельны.
Неясно, откуда может взяться прямая, которой перпендикулярны и ВМ и NД, а также как и прямая, которой обе эти прямые параллельны. Не видно и накрест лежащих углов, образовавшихся при пересечении ВМ и NД, равенство которых можно установить. Но вот если догадаться, например, провести диагональ ВД! Тогда доказав, что равны накрест лежащие углы 1 и 2, образовавшиеся при пересечении прямых ВМ и ДN прямой ВД, мы решим задачу. Теперь подумаем, как установить равенство углов. Впрочем, способов для этого не так уж много. И самый естественный из них - доказать равенство треугольников МВД и ВNД, углами которых они являются.
У этих треугольников ВД - общая сторона, углы NВД и ВNМ равны как накрест лежащие, образованные при пересечении параллельных ВС и АД и секущей ВД, ВN=МД, так как ВС=АД и СN=АМ. Треугольники равны по двум сторонам и углу между этими сторонами. Цепочка выводов, идущая от условия, замкнулась цепочкой выводов, ведущих к заключению.
Заметили отличие от того, что написано в учебнике и что делается обычно? Оно состоит в том, что ученику не навязывается готовое решение, а он сам становится активным участником его поиска.