Проблемное обучение на уроках информатики и разработка урока к данной теме
ВВЕДЕНИЕ
Современное общество предъявляет серьезные требования к качеству образования молодого поколения: владение различными способами деятельности (познавательной, творческой), умение ориентироваться в огромном информационном потоке, обладание способностью к самостоятельному конструированию своих знаний, умение критически мыслить, владение навыками коллективного труда и т.д. Все эти способности трудно развивать, используя только обычную фронтальную форму проведения уроков. В монографии Е.С. Полат указывается, что “метод проектов - не новое явление в педагогике. В последнее время этому методу уделяется пристальное внимание во многих странах мира. Первоначально его называли методом проблем, и связывался он с идеями гуманистического направления в философии и образовании, разработанными американским философом и педагогом Дж. Дьюи. Он предлагал строить обучение на активной основе через целесообразную деятельность ученика, сообразуясь с его личным интересом именно в этом знании. Отсюда чрезвычайно важно было показать детям их личную заинтересованность в приобретаемых знаниях, которые могут и должны пригодиться им в жизни”. При решении задач ученики сталкиваются с проблемными ситуациями, явно или смутно осознаваемыми. Во время работы над задачей в подборе материала активно используется наблюдение, выдвигаются гипотезы, идет экспериментальная их проверка, разрешается интерес, проблемность ситуации.
Проблемная ситуация в образовательном пространстве
Содержит ТРИ главных компонента:
а) потребность учащегося в новом знании или способе действия (“хочу узнать…, научиться…”);
б) неизвестное знание, которое учащийся должен усвоить по проекту педагогических целей;
в) известные знания и сформированные умения (могу сам, без педагога), усвоенные в ходе предшествующей учебы.
Создается на материале:
а) из истории науки и промышленности;
б) описаний ситуаций профессиональной деятельности;
в) альтернативных методов решения профессиональных задач.
Проблемная ситуация включает в себя положение, содержащее противоречие и не имеющее однозначного решения; особое психологическое состояние познающей личности, характеризующееся возникновением познавательной потребности:
1) Проблемная ситуация побуждает его искать новый способ объяснения или действия.
2) Ученик не может достичь цели с помощью известных ему (из ранее изученных) способов действия.
3) Интеллектуальное затруднение, которое возникает у ученика, когда он не знает, как объяснить какое-либо явление, факт, процесс действительности и как действовать при этом.
4) Проблемная ситуация создается проблемным формулированием вопросов, задач, заданий, заданий поискового характера.
Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную деятельность учащихся по их разрешению, в результате чего и происходит творческое овладение профессиональными занятиями, навыками, умениями и развитие мыслительных способностей.
Ребенок усваивает материал, не просто слушая или воспринимая органами чувств, а как результат удовлетворения возникшей у него потребности в знаниях, являясь активным субъектом своего обучения.
Условиями успешности обучения являются:
- проблематизация учебного материала (знания – дети удивления и любопытства);
- активность ребенка (знания должны усваиваться легко);
- связь обучения с жизнью ребенка, игрой, трудом.
Особенности содержания
Проблемное обучение основано на создании особого вида мотивации - проблемной, поэтому требует адекватного конструирования дидактического содержания материала, который должен быть представлен как цепь проблемных ситуаций.
Проблемные ситуации могут быть различными по содержанию неизвестного, по уровню проблемности, по виду рассогласования информации, по другим методическим особенностям (рис 1).
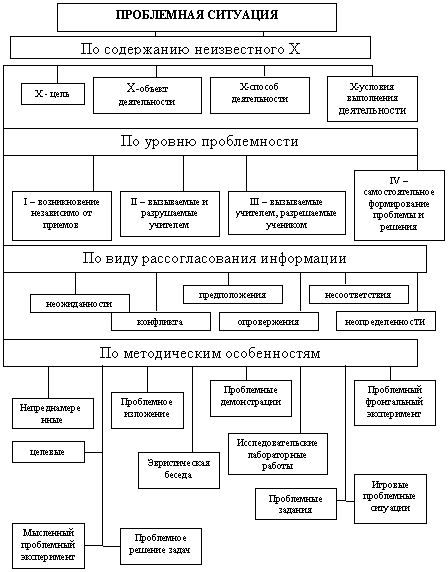
Особенности методики
Проблемные методы – это методы, основанные на создании проблемных ситуаций, активной познавательной деятельности учащихся, состоящей в поиске и решении сложных вопросов, требующих актуализации знаний, анализа, умения видеть за отдельными фактами явление, закон.
В современной теории проблемного обучения различают два вида проблемных ситуаций: психологическую и педагогическую. Первая касается деятельности учеников, вторая представляет организацию учебного процесса.
Педагогическая проблемная ситуация создается с помощью активизирующих действий, вопросов учителя, подчеркивающих новизну. Создание психологической проблемной ситуации сугубо индивидуально. Ни слишком трудная, ни слишком легкая познавательная задача не создает проблемной ситуации для учеников. Проблемные ситуации могут создаваться на всех этапах процесса обучения: при объяснении, закреплении, контроле.
Создавая проблемную ситуацию, я направляю учащихся на ее решение, организую поиск решения. Таким образом, ученик ставится в позицию субъекта своего обучения и как результат у него образуются новые знания, он овладевает новыми способами действия. Трудность управления проблемным обучением состоит в том, что возникновение проблемной ситуации – акт индивидуальный, поэтому я использую дифференцированный и индивидуальный подход.
Методические приемы создания проблемных ситуаций:
- подвожу учащихся к противоречию и предлагаю им самим найти способ его разрешения;
- излагаю различные точки зрения на один и тот же вопрос;
- предлагаю классу рассмотреть задачу с различных позиций;
- делаю сравнения, обобщения, выводы из ситуации, сопоставляю факты;
- ставлю конкретные вопросы (на обобщение, обоснование, конкретизацию, логику рассуждения);
- определяю проблемные теоретические и практические задания (например, исследовательские);
- ставлю проблемные задачи (например, с недостаточными или избыточными исходными данными, с неопределенностью в постановке вопроса, с противоречивыми данными, с заведомо допущенными ошибками, с ограниченным временем решения, на преодоление “психологической инерции”).
Для реализации проблемной технологии необходимы:
- отбор самых актуальных, сущностных задач;
- определение особенностей проблемного обучения в различных видах учебной работы;
- построение оптимальной системы проблемного обучения, создание учебных и методических пособий и руководств;
- личностный подход и мастерство учителя, способные вызвать активную познавательную деятельность ребенка.
Проблемно – поисковая (исследовательская) педагогическая технология
Проблемно- поисковая технология в обучении включает в себя создание особого пространства учебной деятельности, в котором ученик в учебном процессе совершает субъективное открытие закона, явления, закономерности; осваивает способ познания и механизм приобретения новых знаний о действительности.
Модель организации учебного процесса называют “ОБУЧЕНИЕ через ОТКРЫТИЕ”.**
Модель организации учебного процесса строится на реализации принципа проблемности в обучении.
Принцип проблемности реализуется:
- как в содержании учебного предмета;
- так и в процессе развертывания этого содержания в учебном процессе.
Технологические приемы организации учебного процесса.
а) создать в пространстве деятельности ученика значимую для него проблемную ситуацию;
б) наполнить проблемную ситуацию противоречивостью в состоянии исследуемого объекта и создать условия для осознания этого противоречия учеником как проблемы;
в) сформулировать задачу продуктивного (или творческого) типа, вытекающую из осознанной учеником проблемы.
Результативность.
Результативность можно оценить с помощью критериев:
а) наличие у ученика положительного мотива к деятельности в проблемной ситуации
(“Хочу разобраться, хочу попробовать свои силы, хочу убедиться смогу ли разрешить эту ситуацию…);
б) наличие у учащихся положительных изменений в эмоционально - волевой сфере
(“Испытываю радость, удовольствие от деятельности, мне это интересно, могу с усилием воли концентрировать свое внимание…”);
в) переживание учащимися субъективного открытия
(“Я сам получил этот результат, я сам справился с этой проблемой, я вывел закон…”);
г) осознание учеником усвоения нового как личностной ценности
(“Лично мне это нужно, мне важно научиться решать эти ситуации, мне будут эти знания нужны…”);
д) овладение обобщенным способом подхода к решению проблемных ситуаций: анализом фактов, выдвижением гипотез для их объяснения, проверкой их правильности и получением результата деятельности.
Признаки применения подхода в учебном процессе.
Методы обучения – проблемные:
а) проблемного изложения;
б) частично-поисковый;
в) исследовательский;
Формы организации учебного пространства коллективные:
а) парное взаимодействие;
б) микро групповое взаимодействие;
в) групповое взаимодействие;
г) межгрупповое взаимодействие.
Развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения - репродуктивной или продуктивной (творческой). Только тогда, когда учебная деятельность, направленная на овладение основами наук и на развитие личностных качеств, сформирована на более высоком уровне, начинает ярко проявляться ее творческая сторона. Потенциальные возможности почти всех школьников высоки, а также развита творческая деятельность учащихся. Но необходимо рационально организовать учебный процесс. Сюда включается логико-содержательное построение материала, и создание проблемных ситуаций, и частично-поисковый или исследовательский метод обучения. Но какой бы метод обучения мы не избирали, успех в конечном итоге зависит от успешного протекания творческого процесса.
Творческая деятельность ученика, направленная на творческое понимание усваиваемого материала и порождение новых способов действия, ее развития зависит от наличия трех составляющих мышления:
- высокий уровень сформированности элементарных мыслительных операций: анализа и синтеза, сравнения, аналогии, классификации;
- высокий уровень активности, проявляющийся в выдвижении множества гипотез, вариантов решений, нестандартных идей;
- высокий уровень организованности и целенаправленности мышления, проявляющихся в выделении существенного в явлениях, осознании собственных способов мышления.
Сформированность этих качеств мышления позволит преодолеть трудности в овладении учебным материалом и приведет к развитию творческой личности учащегося.
Таким образом, задача учителя сводится к формированию указанных компонентов мышления.
Приемов, при помощи которых достигается успешное развитие мыслительной деятельности учащихся, множество. К таким приемам можно отнести ситуации, в которых ученик должен:
1) защищать свое мнение, проводить в его защиту аргументы, доказательства, использовать приобретенные знания, уметь решать нестандартные задачи;
2) задавать вопросы учителю, товарищам, выяснять непонятное, углубляться с их помощью в процесс познания;
3) рецензировать ответы товарищей, вносить коррективы, давать ответы, видеть и действовать в уме;
4) делиться своими знаниями с другими;
5) побуждать учащихся находить не единственное решение, а несколько;
6) создавать ситуации самопроверки, анализа собственных познавательных и практических действий;
Разработка урока реализации идей проблемного обучения
при изучении программирования дана в приложении по теме:
“Ветвления и циклы”
Обучение решению задач различными способами является одной из важнейших составляющих в обучении информатике, так как задачи способствуют развитию мышления и творческой активности учащихся.
При решении задач только одним способом у учащихся единственная цель - найти правильный ответ. Если же требуется применить при этом несколько способов, школьники стараются отыскать наиболее оригинальное, красивое, экономичное решение. Для этого они вспоминают многие теоретические факты, методы и приемы, анализируют их с точки зрения применимости к данной в задаче ситуации, накапливают определенный опыт применения одних и тех же знаний к различным вопросам.
Все это активизирует мыслительную деятельность школьников, прививает интерес к предмету.
Я учу школьников, анализируя условие задачи, делать различные попытки решения, используя имеющиеся у них в запасе методы и приемы. Обычно, в классе задача решается одним или двумя способами. Поиск других способов дается на дом. Учащиеся с большим интересом и увлеченностью выполняют такие задания, находятся в постоянном логическом поиске, который, в свою очередь, развивает исследовательские способности учащихся.
Проблемно - поисковая технология не просто требует от меня, как от учителя изложения знаний в определенной системе, а предполагает также учить школьников мыслить, искать и находить ответы на поставленные вопросы, добывать новые знания, опираясь на уже известные. Учебная дисциплина, в том числе и информатика, должна рассматриваться не как предмет с набором готовых заданий, а как специфическая деятельность человека. Обучение же должно в разумной мере проходить в форме повторного открытия, а не простой передачи суммы знаний.
ЗАКЛЮЧЕНИЕ
Познавательные процессы эффективно развиваются лишь при такой организации обучения, при которой школьники включаются в активную поисковую деятельность. Поиск нового составляет основу развития воли, внимания, памяти, воображения, мышления.
Эффективным средством обучения и развития является организация учебных исследований, цель которых состоит в том, чтобы помочь учащимся открыть новые знания и способы деятельности, углубить и систематизировать изученное.
Каждая новая проблема не всегда вызывает интерес у учащихся. Порой у ребят проявляется страх перед трудностями, неумение преодолевать их самостоятельно. В таком случае нужна задача, которая на первый взгляд, кажется, простой, а на деле требует нестандартного подхода, который создает проблему. При поиске этой проблемы ученик сталкивается с ее исследованием и обобщением.
Возникновение интереса к информатике у значительного числа учащихся зависит в большей степени от того, насколько умело будет построена учебная работа. Обычно задачи повышенной сложности исследовательского характера даются в конце урока. Благодаря своей оригинальности такие задачи сами по себе побуждают учащихся к размышлениям. Получив задание на уроке, учащиеся продолжают поиск решения задачи дома. На следующем уроке один из них объясняет решение задачи всему классу.
Благодаря такой работе у ученика снимается психологический барьер перед поиском решения задачи. Зная, что задача может быть решена разными способами, он смелее будет браться за ее решение. Постепенно, решая задачу за задачей, он приобретает некоторый опыт, что позволит ему развивать логическое мышление.
Подробный разбор способов задач является хорошим подспорьем для того, чтобы освежить в памяти пройденный материал. Накопившиеся знания не будут лежать мертвым грузом, их постоянно нужно использовать. Использование же этих знаний на практике является творческой работой, при которой школьники учатся действенно применять теорию на практике.
При такой работе над задачей формируется логическое мышление учащихся, развивается интуиция, систематизируются знания, расширяется общеобразовательный кругозор, накапливается полезный опыт. Учащиеся овладевают основными методами решения задач, составляющими важную часть многих эвристических алгоритмов, учатся рационально планировать поиск решения задачи, выполнять полезные преобразования условия задачи.
ЛИТЕРАТУРА
1. Зотов Ю. Б. Организация современного урока М., “Просвещение” 1999 г.
2. Сиденко А. С., Сологуб В. А. 100 педагогических технологий. Академия повышения квалификации Минобразования РФ М., 2001 г.
3. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М., 2000 г.
4. Полат Е. С., Телекоммуникации в учебно-воспитательном процессе школы. // Методическое пособие. М, 1993
5. Семакин И., Залогова А., Русаков С., Шестакова Л. Информатика: Учебник по базовому курсу. М.: Лаборатория базовых знаний, 1998.
ПРИЛОЖЕНИЕ
Цель урока:
1. Обобщить и систематизировать знания учащихся по данной теме.
2. Продолжить формировать практические навыки по составлению блок схем и программ.
3. Показать взаимосвязь математики и информатики. Научить использовать знания, полученные на уроке математики при решении задач по информатике.
4. Развивать логическое мышление, умение обобщать, сопоставлять и применять полученные знания на практике.
5. Развивать познавательную деятельность учащихся, прививать интерес к составлению программ, развивать умение анализировать происходящие изменения в решении задач.
Воспитательные цели:
1. Развивать познавательный интерес, творческую активность, интеллект.
2. Развивать интуицию, эрудицию, самостоятельность в суждениях, упорство в достижении цели.
3. Развивать культуру общения, воспитывать внимание, сообразительность, находчивость, тренировку памяти, умение работать в группе.
Тип урока: Комбинированный.
Метод: Проблемно – поисковый метод при решении задач по информатике.
ХОД УРОКА
Учитель: В начале урока я предлагаю следующую задачу для решения в классе: Найти наибольшее число из трех заданных чисел. На доске записываю несколько троек чисел: 568, 742, 390.
Учащиеся называют максимальное число: 742.
Вопрос: “Каким образом вы определили, что данное число максимальное?”.
Если это первые уроки программирования, то учащиеся затрудняются ответить на этот вопрос, поскольку они еще не привыкли отслеживать свои действия при решении задач. Надо помочь дополнительными вопросами, в поисках верного ответа:
Учитель: Мы сравнили числа друг с другом.
Учитель: А как на уроке математике вы бы сравнили натуральные трехзначные числа?
Ответ: Посмотрели разряд числа – если единицы разрядов сотен равны, то сравниваем единицы разрядов десятков, если они равны, сравниваем разряд единиц и больше то число, у которого разряд сотен больше.
Вывод: Итак, максимальное число: 742
Проблема: “А как компьютер сравнит три числа?”
Я обращаю внимание ребят, что машина может сравнивать только два числа
Обозначим одно число буквой А, второе число буквой B, третье число – буквой С.
Учащиеся: Предлагают такой вариант решения проблемы: надо сравнивать первые два числа, а затем, большее из них с третьим числом.
Учитель: Нарисуйте в тетради блок – схему для сравнения трех чисел.
Учащиеся в тетради рисуют блок – схему, а затем сравнивают составленную ими схему с блок - схемой на доске. Одному из учащихся предлагаю сделать анализ блок – схемы. А теперь в соответствии с блок – схемой составьте – программу.
Учащиеся самостоятельно составляют программу.
Учитель: Проверьте правильность работы программы, введите заданные числа и посмотрите результат.
Проблема: А может ли измениться исходное значение переменной А в процессе работы программы?
Ответ: Да.
Учитель: А как? Ответ обоснуйте.
Решение:
1. Находим наибольшее из первых двух данных чисел A и B, а затем – максимальное из полученного числа и третьего данного числа С.
Program MAX1;
Var A, B, C, max: real;
begin
writeln (‘Введите три числа A, B, C’);
readln (A, B, С);
if A>B then max:=A else max:=b;
if C > max then max:=C;
writeln(‘Максимальное значение=’,max);
end.
Учитель: Как вы думаете, можно ли решить задачу другими способами?
Учащиеся получают задание на уроке и продолжают поиск решения задачи.
Предполагаемые решения учащихся:
2 способ. При решении задачи можно проверить, является ли первое число A максимальным и если не является, то сравниваем второе и третье число B и C.
Program MAX2;
Var A, B, C, max: real;
begin
writeln (‘Введите три числа A, B, C’);
readln (A, B, С);
If (A>B) and (A>C) then max:=A;
if B>C then Max:=B else Max :=C;
Writeln(‘Максимальное значение =’, Max);
End;
3 способ. Можно решить задачу, сравнивая попарно все числа .
Program MAX3;
var A, B, C, Max: real;
begin
Writeln(‘Введем три числа’);
readln(A, B, C);
If (A>B) and (A>C) then Max:= A;
If (B>A) and (B>C) then Max:=B;
If (C>A) and (C>B) then Max:=C;
Writeln(Max:6:2);
end.
Чтобы убедиться в правильности выполнения программы, желательно рассмотреть ее выполнение с помощью таблицы значений. При проверке правильности выполнения программы необходимо рассматривать все возможные варианты А>В>С, А>С>В, В>С>А, С>В>А, В>А>С, С>А>В.
Проблема: А можно написать программу, чтобы она выстраивала числа в порядке возрастания или убывания?
Ученики предлагают свои варианты решения данной проблемы.
Варианты решения задачи:
Программа выстраивает числа в порядке убывания.
Program MAX4;
Var A, B, C, Max: real;
begin
Writeln(‘Введите три числа’);
Readln(A, B, C);
If (A>B) and (A>C) and (B>C) then writeln (A, ‘ ‘,B,’ ‘,C);
If (B>C) and (B>A) and (A>C) then writeln (B, ‘ ‘,A,’ ‘,C);
If (C>A) and (C>B) and (A>B) then writeln (C, ‘ ‘,A,’ ‘,B);
If (A>B) and (A>C) and (C>B) then writeln (A, ‘ ‘,C,’ ‘,B);
If (B>C) and (B>A) and (C>A) then writeln (B, ‘ ‘,C,’ ‘,A);
If (C>A) and (C>B) and (B>A) then writeln (C, ‘ ‘,B,’ ‘,A);
End.
Программа печатает максимальное число, минимальное число и среднее число.
Program MAX5;
Var A, B, C, Max, Min, Sr : real;
begin
Writeln(‘Введите три числа’);
Readln(A, B, C);
If A>B Then Max:=A else Max:=B;
If C> Max Then Max:=C;
If A<B Then Min:=A else Min:=B;
If C< Min Then Min:=C;
If (A>B) and (A<C) Then Sr:=A;
If (B>A) and (B<A) Then Sr:=B;
If (C>A) and (C<B) Then Sr:=C;
If (B<A) and (B>C) Then Sr:=B;
If (A<B) and (A>C) Then Sr:=A;
If (C<A) and (C>B) Then Sr:=C;
Writeln (‘Max=’, Max:6:2);
Writeln (‘Sr=’, Sr:6:2);
Writeln (‘Min=’, Min:6:2);
End.
РАССМОТРИМ ЗАДАЧУ № 2.
Даны три натуральных числа. Найти их наибольший общий делитель.
Вопрос: Какие существуют методы нахождения НОД?
Ответ: Существуют различные методы нахождения наибольшего общего делителя нескольких натуральных чисел:
1. разложения на простые сомножители,
2. алгоритм Евклида,
3. целочисленное деление.
Найти НОД чисел 48, 36, 24
Разложим на множители числа:
48 = 2 * 2 * 2 * 2 *3
36 = 2 * 2 * 3 * 3
24 = 2 * 2 * 2 * 3
Из множителей вычеркиваем те, которые не входят в разложение второго и третьего числа
– это числа 2 * 2 * 3 =12
Учитель: Сделайте вывод для тройки чисел x, y, z.
Проблема: Какие же знания и умения необходимы для построения алгоритма нахождения НОД?
Для того чтобы построить алгоритм, необходимо уметь:
- определять все простые множители в пределах заранее неизвестных чисел х и у, z;
- хранить эти простые множители и обращаться к ним;
- хранить все сомножители для чисел х и у, z;
- выбирать из трех множеств одинаковые элементы.
Сделайте анализ.
Каждая часть задачи сложна для алгоритмизации. Построение массива простых чисел требует проверки, является ли число простым, т.е. не делится ли оно на все простые числа, меньше данного.
Второй метод решения – рекурсивный. Его общепринятое название – алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел.
НОД (х, у) вычисляется в соответствии со следующим правилом:
НОД (х, у)= 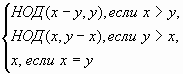
Мы разбирали решение задачи для нахождения НОД двух чисел.
Для решения данной задачи воспользуемся циклом с постусловием.
Третий метод решения – это целочисленное деление.
Пусть х и у – одновременно не равные нулю целые неотрицательные числа, и пусть х![]() у. Если у = 0, то НОД (х, у) = х, а если у
у. Если у = 0, то НОД (х, у) = х, а если у![]() 0, то для чисел х, у и r, где r остаток от деления х на у, выполняется равенство НОД (х, у) = НОД (у, r).
0, то для чисел х, у и r, где r остаток от деления х на у, выполняется равенство НОД (х, у) = НОД (у, r).
В соответствие со следующим правилом:
НОД(48, 18) = НОД(18, 12) = НОД(12, 6) = 6.
Первое число делим нацело на второе. Очевидно, что остаток целочисленного деления меньше второго числа. Если остаток равен нулю, то это значит, что первое число нацело делится на второе, и в этом случае второе число и будем считать НОД (в соответствие с определением). Если остаток не равен нулю, то заменим первое число на второе, а второе – на остаток, и будем повторять действия до тех пор, пока остаток не станет равным нулю.
Запишем алгоритм решения задачи:
1. Ввод натуральных чисел х, у.
2. Найдем r – остаток от деления х нацело на у.
3. Если r = 0, то найдем значение у, иначе х:=у; у:= r.
4. Найдем r – остаток от деления х нацело на у.
- Вычислить значение х
- Порядок действий имеет большое значение. Результат выполнения операций x:=x; y:=r отличен от результата выполнения операций
y: = r; x: =y.
Проблема: А правильно ли мы составили алгоритм?
Задание на дом: Докажите правильность алгоритма.
Решение задачи для нахождения НОД двух чисел.
Program NOD_1;
Var x, y:integer;
Begin
Writeln(‘Введите два числа’);
Readln (x, y);
Repeat
If x > y then x:= x mod y else y:= y mod x;
Until (x = 0) or ( y = 0);
{до тех пор, пока одно из чисел не станет равно нулю}
Writeln (‘НОД=’, x + y);
{ Вывод НОД. Одно из чисел обязательно равно нулю}
Readln;
End.
Машина может находить НОД двух чисел.
Проблема:
Как составить программу для нахождения НОД трех?
Учащиеся:
Сначала находим НОД двух чисел, а затем находим НОД третьего числа.
НОД (a, b, c) = НОД (НОД(a, b), c).
Я предлагаю ученикам самим решить задачу.
Один из способов решения задачи, предлагаемый учениками приведен ниже.
Программа на Паскале:
Program NOD_2;
Var A, B,C, S:integer;
Begin
Readln(A, B, C);
Repeat
If A>B then A:=A mod B
Else B:=B mod A;
Until (A = 0) or ( B = 0);
Writeln (‘НОД=’, A + B);
S:=A + B;
Repeat
If S> C then S:= s mod C else C:= C mod S;
Until (S = 0) or ( C = 0);
Writeln (‘НОД=’, S + C);
{Вывод НОД. Одно из чисел обязательно равно нулю
Readln;
End.
Предложенные методы и соответствующие им алгоритмы существенно не различаются, но для конкретных выбранных значений обнаруживается существенная разница в количестве операций при решении задачи. Оценить заранее, какой метод будет эффективнее для конкретных исходных данных, не возможно, так, как нельзя оценить, сколько раз будет выполняться тело цикла (количество повторов).
Для учеников проблема состоит еще и в том, чтобы выбрать метод, который будет более эффективен и прост в решении.
Домашнее задание:
1) Написать программу вычисления нахождения максимального числа из трех заданных чисел.
2) Найти НОД трех чисел любым удобным для вас способом.