Игры и задания занимательного характера на уроках математики
Очевидно, что изучение математики не может и не должно проходить в виде череды игр или забавных, занимательных заданий. Серьезность предмета, объём и сложность изучаемых тем не предполагают постоянного использования только методов, связанных с подачей материала в игровой форме. Но, с другой стороны, сухость изложения, однообразность и неинтересное содержание заданий, чрезмерная серьезность на уроках могут привести к потере интереса к предмету. Особенно в 5-6-х классах целесообразно вводить в урок элементы занимательности в виде исторических экскурсов, творческих заданий, необычных по форме или по содержанию задач, игр. Практика показывает, что использование на уроках элементов занимательного характера позволяет значительно повысить интерес учащихся к предмету, снизить утомляемость, развивает творческие способности учеников, улучшает психологический климат на уроке и межличностные отношения в коллективе.
Не следует использовать один и тот же прием постоянно, чтобы избежать привыкания и снижения интереса. Разнообразие форм и объемов занимательных элементов дает возможность построить каждое занятие таким образом, чтобы при сохранении серьезности подхода к изучению предмета создать положительную эмоциональную обстановку в классе, повысить мотивацию изучения математики.
Из своей практики приведу несколько примеров использования занимательных заданий и игровых уроков.
ЗАНИМАТЕЛЬНЫЕ ЗАДАНИЯ
1. В виде необычных по содержанию или по форме вопросов или задач, не требующих объемных выкладок и вычислений.
В начале урока или перед изложением основного материала для концентрации внимания и создания положительного настроя в классе. Например:
1) Простые задачи, требующие при решении внимания. Например: "5 мудрецов за 5 дней решают пять задач. Сколько задач решат 10 мудрецов за 10 дней?"
2) Задания с "магическими квадратами".
3) Задачи от лица некоего персонажа. Например: Радикал Квадратурович Многогранников:
"Квадрат со стороной а нужно заменить двумя такими квадратами, суммарная площадь которых равна площади данного квадрата. Если один из них имеет сторону, равную половине а, то какой должна быть сторона второго квадрата?"
4) В разных классах по мере изучения различных тем:"Записать натуральное число в виде":
| - обыкновенной дроби; | - обыкновенной дроби с заданным знаменателем; |
| - квадратного корня; | - корня заданной степени; |
| - в виде степени; | - в виде степени с заданным показателем; |
| - в виде степени с заданным основанием; | - в виде логарифма; |
| - в виде логарифма заданного числа; | - в виде логарифма с заданным основанием |
Сразу после объяснения нового материала для закрепления полученных сведений:
1) При изучении действий (умножение и деление) с рациональными числами:
"Могут ли два числа быть одновременно и противоположными, и взаимно обратными?"
2) При изучении темы "Pавносильные уравнения", правила равносильных переходов,
| предлагаю детям софизм: | 25-15-10 = 20-12-8 - верно, |
| вынесем общий множитель за скобку: | 5(5-3-2) = 4(5-3-2); |
| Разделим обе части уравнения на одно и то же число (5-3-2): | 5 = 4 - неверно. |
В чем ошибка, которая привела к неверному результату?
3) при изучении темы "Квадратные корни" в 8-м классе после определения арифметического квадратного корня вопрос: "Какое из чисел больше и во сколько раз: а) 25 и 5? б) 5 и ![]() ?" и т.д.
?" и т.д.
2. Самостоятельные работы, предложенные в занимательной форме. Элемент занимательности может содержаться во внешней форме (необычность внешнего оформления задания) или в содержании самих заданий. Работы можно предлагать и для выполнения на уроке, и в качестве домашнего задания. Например:
А. Классные самостоятельные работы:
1) 5 кл.
а)
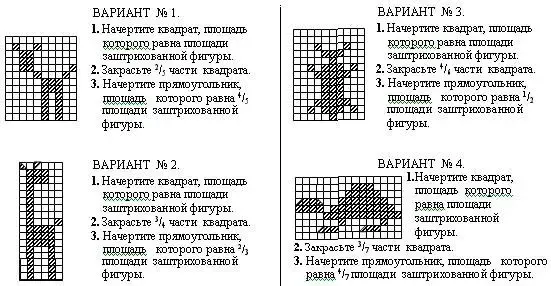
б)

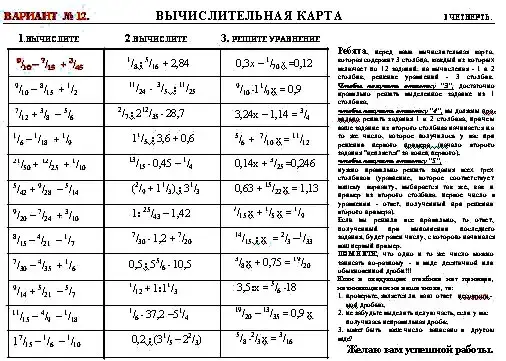
2) 6 кл.
Классная самостоятельная работа "Вычислительная карта" используется многократно (12 вариантов) для тренировки счета. Обычно даю эту работу в начале урока, если сам урок не содержит других проверочных работ.
Б. Самостоятельные работы, предлагаемые в качестве домашнего задания (приветствуется красочное оформление).
6 класс.
а) По теме "Координаты на плоскости" задание "Рисуем по координатам".
Например 15. КОШКА
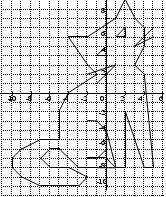
(0;-4); (1;-8); (2;-8); (2;-2); (4;-8); (5;-8); (4;2); (3;3); (4;5); (4;7); (3;8); (2;10); (1;8); (-2;6); (-4;6); (-2;3); (-1;2); (-4;0);(-5;-2); (-5;-5); (-7;-5); (-9;-6); (-10;-7); (-10;-8); (-9;-9); (-7;-10); (-3;-10); (-2;-9); (-4;-8); (-6;-8); (-7;-7);(-6;-6);(-5;-6); (-3;-8); (1;-8); (0;-7); (-2;-7); (-1;-7); (0;-6); (0;-4); (-1;-3); (-2;-3); Глаза: (-1;4); (0;4); (0;5); (-1;4) и (1;6); (2;6); (2;7); (1;6); Усы: (-2;2); (1;3); (-1;1) и (5;7); (3;5); (5;6).
ЧЕРЕПАШКА
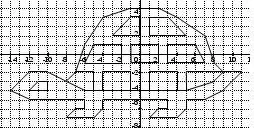
(-8;-3); (-10;-2);(-12;-2);(-14;-4);(-12;-5);(-6;-5); (-6;-6);(-7;-6); (-8;-7); (-5;-7); (-4;-6); (-4;-5); (3;-5); (3;-6); (2;-6); (1;-7); (4;-7); (5;-6); (5;-5); (7;-5); (9;-4); (11;-2); (9;-2); (8;-1);(7;2); (4;4); (2;5); (-1;5); (-4;3); (-6;1); (-7;-2); (-8;-3); (-6;-4); (5;-4); (8;-3); (9;-2); (5;-2); (5;-4); (4;-4); (4;-2); (1;-2); (1;-4); (-1;-4); (-1;-2);(-4;-2); (-4;-4); (-5;-4); (-5;-2); (-7;-2).
Отдельно:(-6;-1);(-5;1);(-2;1);(-2;-1); (-6;-1) и (-1;-1); (-1;1); (2;1); (2;-1); (-1;-1) и (3;-1); (3;1);(6;1); (7;-1); (3;-1) и (-3;2); (-1;4); (0;4);(0;2); (-3;2);и (1;2); (1;4); (3;4); (5;2); (1;2).Глаз: (-12;-4); (-11;-3); (-10;-3); (-10;-4); (-12;-4).
ДИНОЗАВР
(-9;-2); (-12;-2); (-14;-4); (-12;-5); (-10;-5); (-9;-4); (-4;-4); (-4;-6); (-5;-7); (-3;-7); (-2;-6);(-2;-3); (0;-2);(2;-2);(4;-3);(4;-6);(3;-7);(5;-7);(6;-6);(6;-4);(13;-4);(15;-3); (17;-1); (15;-2); (11;-2);(9;-1);(8;0);(7;2);(5;4);(3;5);(-1;5);(-5;3);(-7;1); (-8;-1); (-9;-2); (-9;-1);(-8;-1);(-8;1); (-7;1);(-7;3); (-5;3);(-5;5);(-3;4); (-3;6);(-1;5);(0;7); (1;5);(2;7); (3;5); (5;6); (5;4); (7;4); (7;2); (8;2); (8;0); (9;0); (9;-1); (11;-1); (11;-2); (12;-1); (13;-2); (14;-1);(15;-2);(15;-1);(17;-1); Глаз:(-12;-4); (-11;-4); (-11;-3); (-12;-4).
ЛЯГУШКА
(4;5);(2;7);(-3;7); (-5;5);(-6;7);(-6;8);(-3;8); (-6;8); (-5;9); (-3;9); (-3;7); (-5;5); (-7;7); (-7;8);(-5;10);(-3;10); (-2;9); (-1;7); (0;7); (1;9); (2;10); (4;10); (6;8); (6;7); (4;5); (5;7); (5;8); (2;8); (5;8); (4;9); (2;9); (2;7); (4;5); (4;4); (3;2); (1;1); (-2;1); (-4;2); (-5;4); (-5;5); (-5;4); (-4;0); (-5;3); (-7;4); (-8;4); (-9;3); (-9;0); (-7;-2);(-11;-2);(-12;-3); (-5;-3);(-5;-2); (-7;1); (-5;-2); (-5;-3);(-4;0); (-5;-3); (-7;-5); (-5;-4); (-6;-7);(-4;-4);(-3;-7);(-3;-4); (-1;-4); (-3;-3);(-2;-1); (-1;0); (0;0);(1;-1); (2;-3);(0;-4); (2;-4); (2;-7); (3;-4); (5;-7);(4;-4);(6;-5); (4;-3); (4;-2); (6;1); (4;-2);(4;-3); (11;-3); (10;-2); (6;-2); (8;0); (8;3);(7;4); (6;4);(4;3); (3;0);(4;-3);(3;0); (4;4);
Отдельно: (3;4); (2;3); (0;2); (-1;2); (-3;3); (-4;4).
СТРЕКОЗА
(5;4);(3;3); (-7;-7);(-7;-8);(-6;-8);(4;2);(5;4);(5;6); (4;6); (3;5); (3;4); (7;4); (7;3); (6;2); (5;2); (5;4); (6;5);(7;5); (6;6); (6;5);
крылышки: (2;2); (2;3); (-7;12); (-8;12); (-8;10); (-6;7); (2;2); (-9;8); (-9;7); (-8;5); (-4;2); (1;1);
крылышки: (3;1); (4;1); (13;-8); (13;-9); (11;-9); (8;-7); (3;1); (9;-10); (8;-10); (6;-9); (3;-5); (2;0).
КРОЛИК

(5;1); (3;2); (1;2); (-1;0);(-1;-2);(0;-3); (2;-3); (0;-4); (-1;-4); (0;-3); (-1;-4); (-2;-5);(-3;-5); (-2;-4); (-1;-4); (-2;-5); (1;-5); (3;-4); (5;-4); (5;-3); (6;-2); (6;-1); (7;-2); (8;-2); (9;-1); (9;0); (8;1); (7;1); (6;0); (6;2);(5;4);(3;5);(0;5);(-2;4);(-4;5); (-1;6);(1;7);(3;9); (5;13); (2;12); (-5;5);(-3;11);(-3;14);(-4;16); (-6;12); (-6;5); (-7;4);(-7;0); (-6;0);(-7;1);(-6;0);(-5;0); (-4;1);(-4;0);(-3;-1);(-4;-4); (-5;-5);(-6;-5); (-5;-4); (-3;-1); (-4;-4);(-5;-5);(-4;-5);(-1;-2);
Глаз: (-6;2); (-5;2); (-5;3); (-6;2);
отдельно: (-3;6); (1;10); (3;11);
отдельно: (-5;6); (-5;11); (-4;13).
АВТОМОБИЛЬ
(9;6); (5;4); (5;5); (4;6); (2;6); (0;5); (-1;3); (-2;0);(-5;-2);(-7;-4);(-8;-4); (-11;-3); (-13;-2); (-14;-1); (-12;1); (-8;3);(-7;5); (-5;7); (2;8); (1;8); (4;6);(1;8); (5;9);(7;9);(9;8); (10;7); (10;5); (8;3); (7;4); (5;3); (4;1); (4;0); (0;-2);(-1;-1);(-3;-2);(-4;-4); (-4;-5); (-7;-6); (-9;-6); (-13;-4); (-14;-3); (-14;-1);
отдельно:(-4;-5);(-3;-6);(-2;-6); (0;-4); (0;-2) и (4;0); (5;-1); (6;-1); (8;1); (8;3) и (-3;1); (-7;3); (-6;5); (-5;6); (-1;4); (-2;3); (-3;1); и (-1;1); (4;4); (4;5); (2;5); (0;4); (-1;1).
ЁЖИК
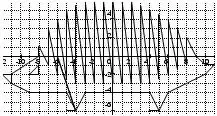
(-11;-2); (-11;-3); (-12;-2); (-11;-2); (-8;0); (-8;1); (-7;-1); (-7;3); (-6;-2); (-6;4);(-5;-2,5); (-5;5); (-4;-3); (-4;5,5); (-3;-3); (-3;6); (-2;-3); (-2;6); (-1;-3); (-1;6); (0;-3); (0;6); (1;-3); (1;6); (2;-3); (2;6); (3;-3); (3;5,5); (4;-3); (4;5); (5;-2,5); (5;4,5);(6;-2); (6;4); (7;-1,5);(7;3); (8;-1); (8;2); (9;0); (10;-1); (11;-1);(10;-2); (6;-4); (5;-6);(4;-6); (5;-6); (4;-4); (-3;-4); (-4;-6); (-5;-6); (-4;-6); (-5;-4); (-9;-4); (-11;-3);
глаз: (-9;-2); (-8;-1); (-8;-2); (-9;-2).
СОБАКА
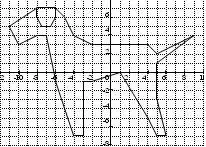
(-4;-7); (-6;-1); (-7;4); (-8;4); (-10;3); (-11;5); (-8;7); (-6;7); (-6;6); (-6,5;5); (-7,5;5); (-8;6); (-8;7); (-6;7); (-5;6); (-4;4); (-2;3); (4;3); (5;2); (9;4); (5;1); (5;-3); (6;-7); (5;-7); (4;-5); (1;0); (-2;-1); (-3;-1); (-3;-7); (-4;-7).
Предлагаю детям придумать самим подобное задание.
б) При итоговом повторении. Решите задачи:
ВАРИАНТ № 1.
1. Собралась Баба Яга на шабаш. Чем удивить подружек? Решила Баба Яга испечь громадный пирог с лягушками. Открыла кулинарную книгу и прочитала, что на приготовление маленького пирожка с лягушками (всего 1,5 кг) требуется 33 лягушки. Стала Баба Яга считать, сколько же лягушек заказать кикиморам, чтобы испечь громадный пирог весом 35 кг, да так до сих пор и считает. Помоги Бабе Яге: посчитай, сколько лягушек потребуется на такой пирог.
2. Не хотела Василиса Прекрасная выходить замуж и задала глупым своим женихам "неразрешимую" задачу: "15 раз по 15 синиц смогут очистить мой лес от гусениц за 15 лет. Сколько лет потребуется 3 раза по 3 синицам, чтобы проделать ту же работу?" А ты сможешь решить эту задачу?
ВАРИАНТ № 2.
1. Имел Царь Василий Пупкин громадное царство, и было в нем 7 лесов и 7 морей. Полжизни воевал Василий, чтобы увеличить свои богатства, и удалось ему расширить свои владения: теперь у него уже 33 леса и 33 моря. Задумался царь, какую же стражу теперь ему требуется содержать, чтобы охранять все это и поддерживать порядок в царстве? Призвал своих мудрецов (а в их числе и ты) и велел посчитать количество стражи: если раньше ему хватало 119 тысяч стражников, то сколько требуется теперь?
2. Спорят Леший с Кикиморой: -Чьё болото? - и пришли за разрешением спора к Бабе Яге, а Баба Яга задала им задачу - кто правильно ответит, тот и владелец болота: "Ваше болото Водяной выпьет за 77 дней, а змей Горыныч имеет голов в 7 раз больше, чем Водяной, да каждая из них пьет в 33 раза медленней. Сколько дней Змею Горынычу пить ваше болото?" Что им отвечать?
ВАРИАНТ № 3.
Ужинали вместе Змей Горыныч и Кощей Бессмертный и решали давний спор: кому свататься к Бабе Яге? Спорили они спорили и решили, что свататься будет тот, кто умнее, и решит задачу другого. Решите эти задачи:
1. Змей Горыныч - Кощею Бессмертному: "Лететь мне от своего царства до Бабы Яги 3 дня и 3 ночи, а расстояние между нами 33 раза по 33 версты. Сколько же мне лететь от своего царства до тебя, если между нами все полные 3993 версты?"
2.Кощей Бессмертный - Змею Горынычу: "Богат я, Змей Горыныч, да нет у меня кареты, чтобы ехать свататься, а мастер просит за карету 144 золотых перстня по 144 унции каждый. Перстни у меня есть, да только мне проще отдать цепями. Сколько же мне нужно отдать цепей, если каждая весит 324 унции?"
ВАРИАНТ № 4.
1. Расчесывает Василиса Прекрасная свои чудесные кудри и считает: "Живу я в этом новом замке уже 25 раз по 25 дней и успела обломать о свои кудри 44 гребня. Сколько же гребней мне заказывать золотому мастеру на следующие 5000 дней?"
2. Решает Водяной вопрос об охране болота, так как многие старые жабы просятся на покой и подросли молодые лягушата. Каждая старая жаба квакает 24 раза в день, и каждый ее квак длится по 2/3 глухариной песни. Молодые лягушата квакают чаще - 33 раза в день, да каждый их квак длится всего 0,1 глухариной песни. Сколько молодых лягушат призвать на действительную службу, чтобы болото охранялось так же оглушительно, если на пенсию подали заявление 33 старых жабы?
3. Тесты с новыми математическими терминами или с именами собственными в ответах. Каждый легко сможет зашифровать в ответах теста из 5 вопросов имена Гаусс, Фалес, Непер, Эйлер, Герон, Фурье, Ферма и т.д. Та же работа приобретает для детей новый интерес, повышается внимание при разборе. Приведу пример тестовой самостоятельной работы в 9-м классе по геометрии.
МАТЕМАТИЧЕСКИЕ ИГРЫ
1) Игры, занимающие небольшую часть урока (10-20мин), способствующие закреплению пройденного материала. Я бы выделила некоторые типы таких игр:
"Сквозная игра" - игра, привычная детям по оформлению и правилам, поэтому не требуется тратить много времени для объяснений. Удобно сконструировать игру таким образом, чтобы была возможность варьировать задания по разным темам, использовать одну и ту же схему и для командного первенства, и для личного. Приведу примеры:
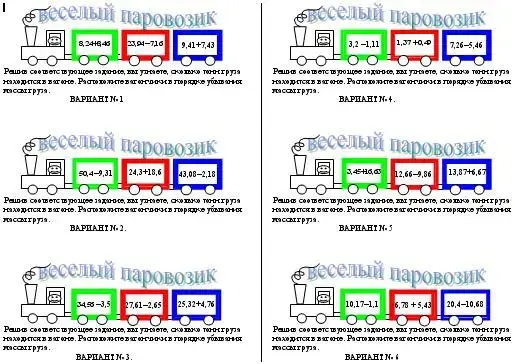
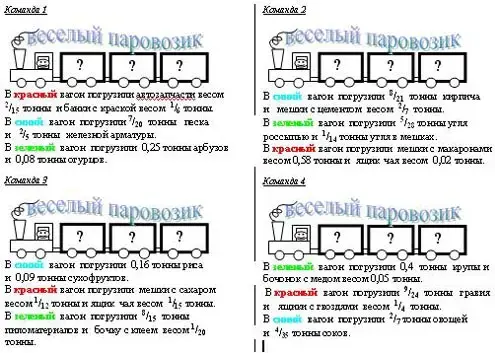
Сквозная игра "Веселый паровозик" может быть использована при изучении практически всех тем 5-6-х классов; может использоваться и в качестве командной, и для определения личного первенства, и в качестве самостоятельной работы на уроке. Шесть вариантов заданий составлены таким образом, что в ответе каждый из них представляет одну из возможных перестановок (пример одного из вариантов игры "Веселый паровозик" - 5-й класс. Сложение и вычитание десятичных дробей). Размножив задания на 30 вариантов, получим, что каждая перестановка представлена пятью вариантами.
К разновидности этой же игры отношу и игры "Железная дорога" и "Бегуны":
Игра "Бегуны" - индивидуальная; 6 класс.
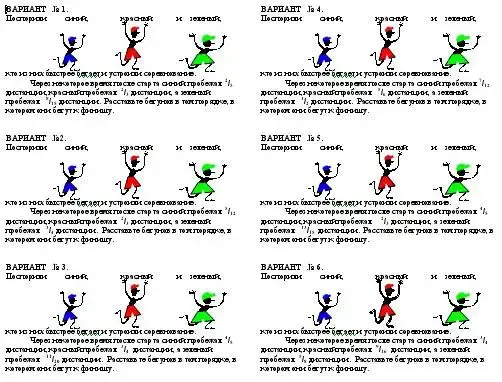
Сравнение обыкновенных дробей. Перед игрой раздаю на каждый стол "Указание...".

Игра "Железная дорога" - командная; 6 класс. Действия с дробями. Задание: Расставьте вагоны таким образом, чтобы первым от паровоза стоял вагон с самым большим количеством груза, за ним - вагон полегче и на самом последнем месте - вагон с наименьшим количеством груза.
Сквозная игра "Угадай по одному вопросу" может быть использована во всех классах при изучении всех тем; возможны домашние заготовки вопросов детьми. Например:
1. 6 класс. На все имеющиеся у меня деньги я могу купить несколько порций мороженого по 8 рублей или несколько пакетов сока по 36 рублей. Задайте 1 вопрос и угадайте, сколько у меня денег.
2. 7 класс. Точка пересечения графиков двух линейных функций находится на оси ординат. Задайте 1 вопрос про коэффициенты к или b этих функций и определите координаты точки пересечения их графиков.
3. 8 класс. Теорема Пифагора. " В треугольнике АВС АВ= 10 см; ВС= 17 см; высота, проведенная из вершины В, равна 8 см. Задайте 1 вопрос и найдите сторону АС." ("Тупым или острым является угол А?")
4. 9 класс. Тригонометрия. "Я задумала угол от 0° до ![]() , синус которого равен косинусу 120° . Задайте 1 вопрос
и угадайте задуманный мною угол." ("Это угол 3 или 4 четверти?")
, синус которого равен косинусу 120° . Задайте 1 вопрос
и угадайте задуманный мною угол." ("Это угол 3 или 4 четверти?")
5.10 класс. Исследование функций. "Некоторая четная функция имеет 5 экстремумов, а график ее производной пересекает ось абсцисс в точках -2; 5 и еще в трех точках. Задайте один
вопрос про знак производной и назовите все минимумы и максимумы данной функции" ("Каков знак производной на любом из промежутков: ![]() ; -5; -2; 0; 2; 5;
; -5; -2; 0; 2; 5;
![]() )
)
6.11 класс. Степенная функция. "У некоторой степенной функции показатель степени неизвестен, но не является натуральным числом. Задайте 1 вопрос и определите, является эта функция возрастающей или убывающей". ("Входит ли 0 в область определения этой функции?")
Игры, заменяющие самостоятельные работы - эти игры, кроме набора заданий математического характера, не содержат никаких других элементов, но их использование позволяет сделать урок значительно более интересным для детей. Примерами таких игр могут служить известные многим игры "Ромашка", "Лесенка" и др., в которых несколько вариантов заданий объединяет одинаковый ответ. К этому же типу игр относится и игра "Цветные карточки", проводимая мной на уроке в 5-м классе при прохождении темы "Умножение и деление натуральных чисел". Отличие этой игры заключается в том, что сложность заданий возрастает по мере их выполнения учеником. Правильно выполнив задание на синей карточке
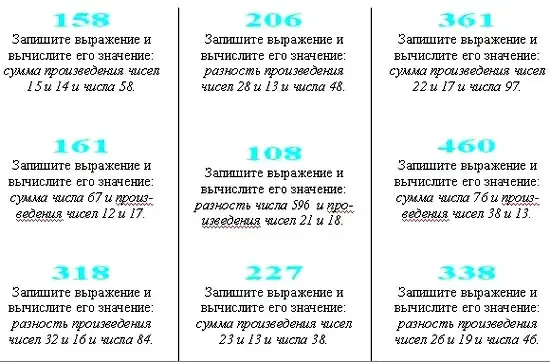
и обеспечив себе удовлетворительную отметку, ученик получает зеленую карточку

с усложненным вариантом задания, а затем красную карточку

- на всех рисунках даны только некоторые примеры заданий. Особая привлекательность этой игры еще и в том, что учитель демонстрирует детям способности "мгновенного счета" при проверке правильности выполнения заданий (на самом деле правильный ответ зашифрован в номере карточки - если к номеру синей и зеленой карточки прибавить 110, то получится правильный ответ; в случае красной карточки следует прибавлять 101.)
Игры, расширяющие кругозор - игры, разные по правилам; при несложной математической части содержат интересные для детей сведения из других дисциплин. Например, командная игра "Планеты" - проводится в 6-м классе для закрепления знаний по теме "Делимость чисел". Кроме проверки и закрепления математических навыков знакомит учащихся с некоторыми сведениями из астрономии, древнегреческой и древнеримской мифологии и истории.
Игра "Планеты". На доске рисунок - солнце и 9 планет без названий.

На весь класс выдаются задания в 4 конвертах: каждое - на команду из 5-6 человек. В конверты вложены: задание и карточки, на одной стороне которых написано число, а на другой - буква.
ВАРИАНТ 1. Из предложенных чисел расставьте в порядке возрастания все четные числа, кратные 9. Переверните карточки и прочитайте название вашей планеты. (Ответ - Нептун).
| С | Н | А | Е | Л | П | Р | Т | О | У | Н | Ю |
| 207 | 36 | 8282 | 216 | 45 | 288 | 99 | 3618 | 6636 | 4446 | 4914 | 1915 |
ВАРИАНТ 2. Из предложенных чисел расставьте в порядке убывания все числа, кратные 2 и 3. Переверните карточки и прочитайте название вашей планеты. (Ответ - Плутон).
| С | И | А | Е | Л | П | Р | Т | О | У | Н | Ю |
| 207 | 33 | 8282 | 316 | 4122 | 4278 | 99 | 3018 | 1536 | 3246 | 1014 | 1915 |
ВАРИАНТ 3. Из предложенных чисел расставьте в порядке возрастания все нечетные числа, кратные 3. Переверните карточки и прочитайте название вашей планеты. (Ответ - Сатурн).
| С | Н | А | Е | Л | П | Р | Т | О | У | И | Ю |
| 207 | 5331 | 216 | 4123 | 4278 | 4299 | 3027 | 1536 | 3255 | 1014 | 1915 | 381 |
ВАРИАНТ 4. Из предложенных чисел расставьте в порядке убывания все числа, кратные 3 и 5. Переверните карточки и прочитайте название вашей планеты. (Ответ - Юпитер).
| С | И | А | Е | Л | П | Р | Т | О | У | Н | Ю |
| 200 | 1335 | 1020 | 3153 | 4170 | 195 | 1125 | 1535 | 3155 | 1010 | 6915 | 185 |
Дети, выполнив задание, узнают название планеты, после чего они получают текст, из которого определяют порядковый номер планеты от Солнца и подписывают свою планету на доске.
1) Нептун - в римской мифологии первоначально бог источников и рек, затем, отождествляемый с грозным Посейдоном, стал почитаться как бог морей. Его супруга - Амфитрита-владычица морей, дочь морского бога Нерея и Дориды. К мужу ее с почетом доставил дельфин, который в благодарность за это был вознесен к звездам. Изображали Амфитриту мчащейся на колеснице, запряженной тритонами, а Нептуна - с трезубцем в руке. В Риме в храме Нептуна ежегодно 23 июля справляли праздник нептуналии с целью предотвращения засухи. Особенно популярны были Нептун и Амфитрита в среде мореходов и всех, кто был связан с морем. Именем бога Нептуна была названа восьмая планета солнечной системы. Она имеет 6 спутников.
2) Сатурн - от латинского "сеять"- бог посевов, один из древнейших римских богов, его супруга Опс - богиня посевов и плодородия. Согласно распространенному мифу, свергнутый Зевсом Сатурн бежал к Янусу, богу всех начал, и получил от него в правление Италию. Сатурн научил жителей земледелию, виноградарству и многим другим полезным занятиям. Италию стали называть "землей Сатурна", а его правление позднее именовали "веком Сатурна" - золотым веком, когда люди жили в равенстве, мире, изобилии. В Риме у Капитолийского холма было воздвигнуто святилище Сатурна. Позднее в храме Сатурна и его супруги Опс хранилась римская казна. В честь Сатурна ежегодно в декабре справляли праздник, во время которого откладывали все дела, делали друг другу подарки, школьникам прощали провинности, повсюду устраивали карнавалы. Именем бога Сатурна была названа шестая планета солнечной системы, имеющая 17 спутников.
3) Юпитер - римский бог неба, дневного света, грозы и молнии, царь богов, отождествленный с древнегреческим Зевсом. Он ведал плодородием, урожаем, дождем, покровительствовал римскому войску, даровал победу, охранял границы, следил за соблюдением клятв и договоров и т.д. С возведением на Капитолийском холме храма Юпитеру он стал почитаться как бог римского государства, его власти и могущества. Главным храмом Рима был храм Юпитера Капитолийского, Юпитера-громовержца, и еще в древности именем Юпитера была названа крупнейшая планета. Юпитер - пятая планета солнечной системы, имеет 16 спутников.
4) Плутон - одно из имен Аида, - владыки подземного мира и царства мертвых. При разделе мира между тремя братьями ему достались подземные владения. Плутон считался божеством подземных богатств и плодородия, дарующим урожай из недр земли. Изображали Плутона могучим мужем, восседающим на троне с двузубцем или жезлом в руке. У ног его обычно лежал трехглавый пес Цербер, который помогал ему охранять царство. Цербер пропускал всех, но никого не выпускал. В царстве Аида протекала река забвения Лета. После глотка воды из нее навсегда забывалась земля и земная жизнь. Отсюда выражение "кануло в Лету" - то есть забыто навсегда. В жертву Плутону приносили быков черного цвета, его отождествляли с древними богами: смерти - Орком, подземного царства - Диспатером. Именем бога Плутона названа девятая планета солнечной системы. Плутон - двойная планета, его спутник, меньший по диаметру, движется на небольшом расстоянии от центра планеты.
В конце игры учитель подписывает остальные планеты и определяет команду-победительницу.
2) Игры, занимающие весь урок.
Обобщающая игра по данной теме - целесообразна при итоговом повторении, когда ученики хорошо изучили тему; способствует закреплению знаний и применению их в нестандартных ситуациях. Например, игра "Лото" при итоговом повторении темы "Квадратные уравнения" в 8-м классе:
Лото "Квадратные уравнения".
Всем ученикам раздаются пронумерованные по вариантам карточки лото с четырьмя заданиями.



Особо успешные ученики могут получить и 2 карточки. Карточки выполнены в стиле карточек лото. Дается 20-25 минут на решение заданий и определение чисел на карточках (решения следует оформлять на отдельных листочках с последующей проверкой учителем).
После этого начинается розыгрыш по принципу игры в лото (можно "вытягивать" по очереди разложенные на столе числа-ответы как билеты на экзамене).
Разыгрывать числа: 0, 1, 2, 3, 4, 5, 7, 9, 10, 584, 585.
Победители получают на уроке "5" (на уроке проверка только на правильность ответов). Все сдают решенные задания и получают отметку, как за самостоятельную работу.
Обобщающая игра по всем пройденным к данному моменту темам - целесообразна при проведении школьной недели математики, если есть возможность выделить целый урок для игры, или при итоговом повторении для закрепления знаний всего курса данной ступени. Весьма распространены и удобны игры типа "Аукцион", "Эрудит", различные викторины, дающие возможность легко варьировать сложность заданий, т.к. не требуют значительной материальной подготовки. Приведу пример командной игры "Олимпиада", проводившейся на неделе математики в 5-м классе.
Игра "Олимпиада". При входе в класс все дети "вытягивают" задание, которое автоматически определяет принадлежность к той или иной команде - "Страны бобров", "Страны лисиц" или "Страны волков". Рассадка происходит по рядам - на каждый ряд садятся участники одной команды; за одним столом - "спортсмены" одного "вида спорта". Ученики начинают выполнять задания и по мере их выполнения проверяют правильность у "судей"; судьи присуждают 1, 2 и 3 места по отдельным видам заданий. Освободившиеся участники команды (правильно решившие свои задания) могут помогать отстающим. На доске изображены тумбы 1,2 и 3 мест по всем трем видам заданий, куда судьи помещают символическое изображение победителей.
Подготовка к игре:
1) подготовка судей (3 чел. - по одному на каждый вид заданий) из успешных учеников класса;
2) изготовление карточек с заданиями.



3) изготовление красочных изображений лисицы, бобра и волка (каждого по 3 шт.) для помещения на тумбы первенства.
Буду рада, если эти материалы пригодятся кому-нибудь из вас в работе.
