По страницам истории математики
1) Первая русская женщина-математик. Какой курьёзный случай повлиял на её интерес к математике?
Софья Васильевна Ковалевская (1850-1891). Впервые С.В. Ковалевская соприкоснулась с математикой ещё в детстве, когда её семья переехала в деревню. Дом, в котором они поселились, отделывали заново, и все комнаты оклеили новыми обоями. Однако на одну из комнат обоев не хватило, и было решено оклеить её простой бумагой. Этой бумагой оказались листы литографированных лекций М.В. Остроградского по дифференциальному и интегральному исчислению. По воспоминаниям С.В. Ковалевской, она могла часами стоять у этой стены, рассматривая листы, «испещрённые странными непонятными формулами», пыталась хоть что-то разобрать, установить тот порядок, в котором листы должны следовать друг за другом. От этого многочасового созерцания многие формулы врезались в её памяти, и когда она, будучи пятнадцатилетней девочкой, брала первый урок дифференциального исчисления у петербургского преподавателя математики А.Н. Страннолюбского, она так скоро усвоила понятия предела и производной, словно наперёд их знала.
2) Математик, составивший первую в России учебную энциклопедию по математике. Как она называлась и в каком году была создана? Известно ли вам её полное название? Какие математические термины ввёл впервые в русский язык автор этой энциклопедии?
Леонтий Филиппович Магницкий (1669-1739). В 1703 году он составил первую в России учебную энциклопедию по математике «Арифметика». Полное название этого сочинения: «арифметика сиречь наука числительная с разных диалектов на славянский язык переведённая и воедино собрана, и на две книги разделена». Введённые Л.Ф. Магницким термины: множитель, делитель, произведение, извлечение корня, миллион, биллион, триллион, квадриллион.
3) Великий русский математик П.Л. Чебышев, будучи студентом, написал работу на конкурсную тему. Как она называлась? Какой инцидент связан с этой работой?
П.Л. Чебышев, будучи студентом четвёртого курса, написал работу «Вычисление корней уравнений». Несмотря на поразительную глубину и новизну подхода к проблеме, названной в заглавии работы, совет университета удостоил эту работу серебряной медалью, в то время как золотую медаль получил студент Анатолий Смоляк, впоследствии никак не проявивший себя в науке.
4) Прибор, представляющий собой вертикальный шест, установленный на ровной горизонтальной площадке, с помощью которого в древности наблюдали за движением Солнца. Как ещё назывался этот прибор? Становлению какой науки способствовали наблюдения с помощью этого прибора?
Гномон. Этот прибор также называли солнечными часами. Он способствовал становлению тригонометрии, так как, изучая изменение длины отбрасываемой гномоном тени, древние неявным образом рассматривали функцию «тангенс». Принято считать, что изобретателем гномона является древнегреческий философ Анаксимандр Милетский (ок. 610-546 до н.э.)
5) Античный математик и астроном, который ввёл деление градуса на минуты и секунды. Какое знаменитое астрономическое сочинение ему принадлежит и из скольких книг оно состоит? В чём суть геометрической теоремы, названной его именем? Известно ли вам, частным случаем какой теоремы она является?
Клавдий Птолемей (ок. 100-170). Ему принадлежит знаменитое сочинение «Альмагест», в котором изложено собрание астрономических знаний Древней Греции и Вавилона, а также построена геоцентрическая модель мира. «Альмагест» состоит из 13 книг, первоначальное его название – «Великое математическое построение по астрономии в тринадцати книгах». В геометрии известна теорема Птолемея, которая гласит: произведение диагоналей вписанного в окружность четырёхугольника равно сумме произведений противолежащих сторон. Эта теорема есть частный случай теоремы Бретшнейдера, которая утверждает: квадрат произведения диагоналей четырёхугольника равен сумме квадратов произведений противолежащих сторон минус удвоенное произведение всех сторон на косинус суммы двух противолежащих углов.
6) Кто впервые доказал формулу Герона? Какие ещё достижения этого учёного вы можете назвать?
Архимед (287-212 до н.э.). Архимеду принадлежат труды: «Об измерении круга», «О квадратуре параболы», «О шаре и цилиндре», «О равновесии плоскости», «О плавающих телах», «О коноидах и сфероидах», «Псаммит (исчисление песчинок)», «О спиралях», «Послание Эратосфену о некоторых теоремах механики». Пользуясь своими оригинальными методами, Архимед вычислял длины кривых, площади поверхностей вращения, площади плоских фигур, объёмы тел, то есть, фактически, предвосхитил идеи современного математического анализа. Он изобрёл машину для орошения полей (архимедов винт), для поднятия тяжестей впервые стал применять систему рычагов и блоков, дал способ определения состава сплавов путём взвешивания в воде и т.д. Ему принадлежит слово «Эврика» (по-гречески, нашёл) – слово, которое он прокричал, выскочив из ванны и побежав голым по улице (открытие знаменитого закона Архимеда). Высказывание – «Дайте мне точку опоры, и я сдвину Землю». На его могиле выгравирован цилиндр, в который вписан шар – Архимед доказал, что объём такого шара занимает две трети объёма цилиндра.
7) Немецкий математик, дававший частные уроки С.В. Ковалевской. Каким забавным случаем было отмечено начало их творческого взаимодействия? Какие открытия этого учёного вы можете назвать?
Карл Теодор Вильгельм Вейерштрасс (1815-1897). В октябре 1870 года к пятидесятипятилетнему Вейерштрассу пришла двадцатилетняя С.В. Ковалевская с просьбой разрешить ей слушать его лекции. Вейерштрасс дал ей несколько трудных задач, надеясь на то, что она больше не появится. Однако, к его большому удивлению, через неделю С.В. Ковалевская принесла ему подробные решения всех этих задач. Учёный был настолько поражён её познаниями, что стал хлопотать о допуске Ковалевской к слушанию лекций в университете. Однако совет университета был неумолим, и Вейерштрасс решил заниматься с ней частным образом. К. Вейерштрасс считается (совместно с О.Коши) основателем математического анализа и теории вещественных чисел. Он положил начало абсолютной строгости в математической теории. Его открытия относятся к теории функции действительной переменной, теории функции комплексной переменной, теории специальных функций, вариационному исчислению, дифференциальной геометрии. Он построил пример всюду непрерывной, но нигде не дифференцируемой функции, создал теорию степенных рядов, строго сформулировал ключевые понятия математического анализа, опираясь на созданную им теорию действительных чисел.
8) Почему константа π получила такое название? Каким методом пользовались учёные для приближённого вычисления числа вплоть до XVII века? Кто является родоначальником этого метода? Какой математик впервые достаточно точно приблизил число π (с 16 верными знаками)? В каком году это было?
Это первая буква в греческом слове «периферия», что в переводе означает «круг». Для приближённого вычисления числа π вплоть до XVII века пользовались следующим методом: вписывали и описывали около окружности многоугольник, вычисляли его периметр, затем удваивали число сторон у обоих многоугольников – ещё раз вычисляли и т.д. Чем больше сторон имели многоугольники, тем точнее их периметры приближали длину окружности. Родоначальником этого метода был Архимед – он показал, что
 .
. Впервые достаточно точно приблизил число π (с 16 верными знаками) математик ал-Каши в своей книге «Об измерении окружности» в 1424 году.
9) В каком году и в связи с какой задачей возникла теория графов?
Теория графов как наука зародилась в 1736 году в связи с поставленной Леонардом Эйлером задачей о семи мостах (или задачей о кёнигсбергских мостах). Суть этой задачи: пройти по семи мостам, не побывав ни на одном из них дважды.

10) С каким математическим понятием связана легенда об изобретении шахмат? Можете ли вы рассказать эту легенду?
Легенда об изобретении шахмат связана с понятием геометрической прогрессии. Суть этой легенды: древнеиндийский математик придумал шахматы и показал своё изобретение правителю страны. Тому так понравилась эта игра, что он пообещал вознаградить изобретателя всем, что бы он ни пожелал. Математик решил получить награду в виде пшеницы, причём на первую клетку шахматной доски попросил положить 1 зерно, на вторую клетку – 2 зерна, на третью клетку – 4 зерна и т.д. сначала правитель даже обиделся за такую скромную просьбу, но на следующее утро он понял, что не сможет рассчитаться с математиком, ибо заказанное им число зёрен равно

Столько пшеницы не найдётся даже на всей планете. По средним подсчётам, для хранения такого количества пшеницы понадобился бы амбар размера 10 км х 10 км х 15 км.
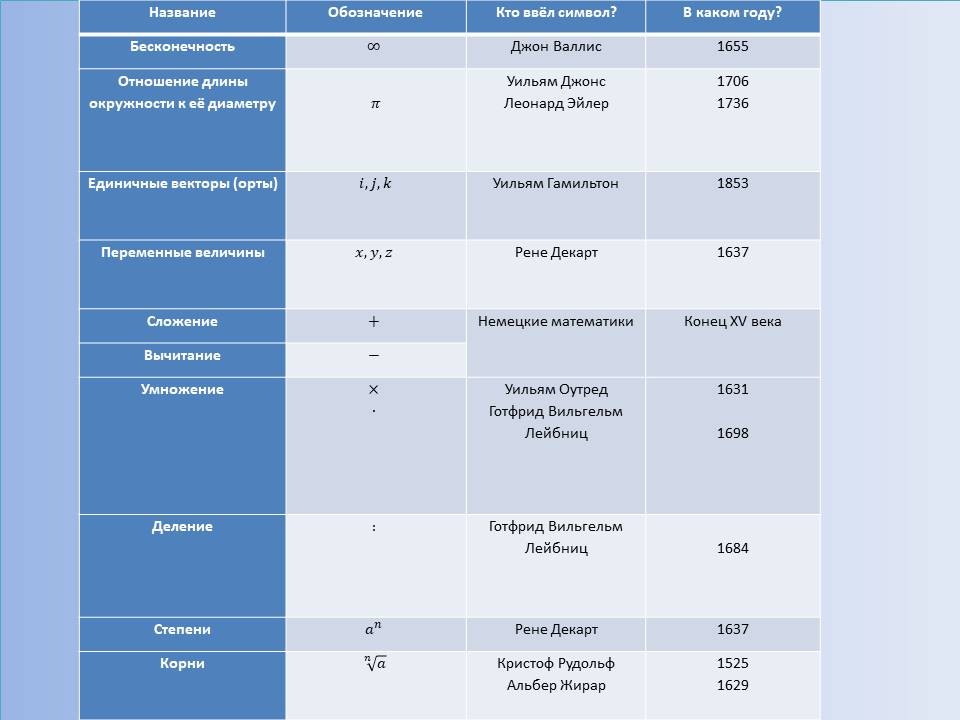
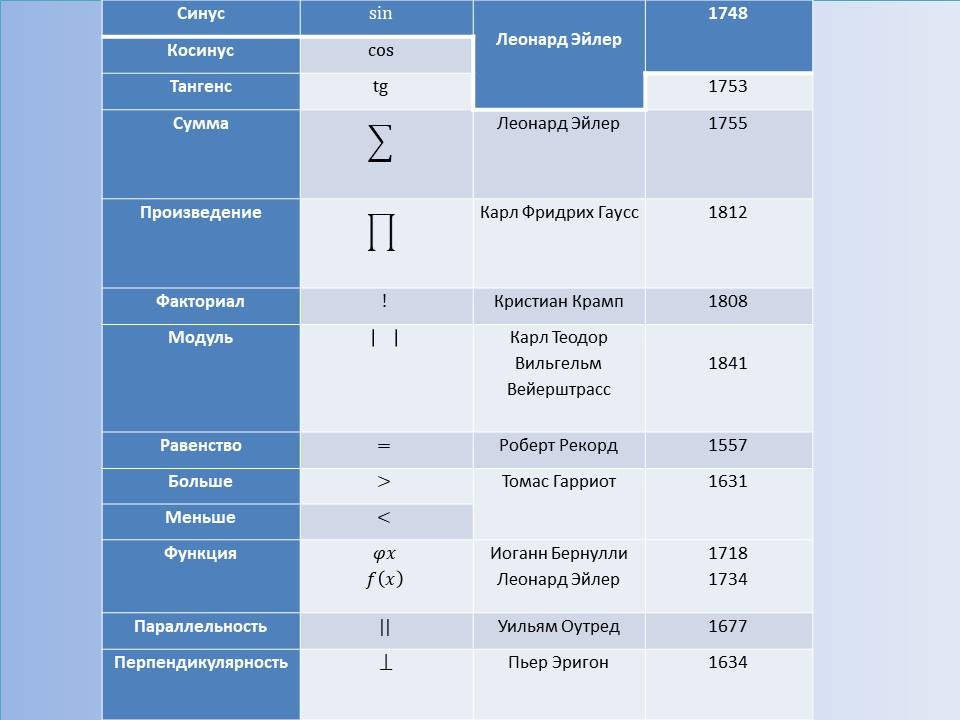
Математическая символика
Кто это сказал?
1) Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий. Русский математик Алексей Иванович Маркушевич (1908-1979).
2) Единственное занятие, которым я поддерживаю необходимое душевное равновесие, это – математика. Немецкий философ Карл Маркс (1818-1883).
3) Математика представляет искуснейшие изобретения, способные удовлетворить любознательность, облегчить ремёсла и облегчить труд людей. Французский математик Рене Декарт (1596-1650).
4) Математика – наука великая, замечательнейший продукт одной из благороднейших способностей человеческого разума. Русский публицист Дмитрий Иванович Писарев (1840-1868).
5) Высшее назначение математики … состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. Американский математик Норберт Винер (1894-1964).
6) Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли. Русский математик Александр Данилович Александров (1912-1999).
7) Арифметика представляет собой логический фундамент всей математики. Французский математик Анри Леон Лебег (1875-1941).
8) Внимательно читая сочинения Архимеда, перестаёшь удивляться всем новейшим открытиям геометров. Немецкий математик Готфрид Вильгельм Лейбниц (1646-1716).
9) Арифметические знаки – это записанные геометрические фигуры, а геометрические фигуры - это нарисованные формулы. Немецкий математик Давид Гильберт (1862-1943).
10) Не считать ничего сделанным, если кое-что ещё осталось сделать. Немецкий математик Карл Фридрих Гаусс (1777-1855).
Занимательные задачи
1) Поставьте знак “+” между некоторыми цифрами числа 987654321, чтобы в сумме получилось 99.
2) Имеется прямоугольник ABCD, смежные стороны которого равны 5 и 12. Из точки A как из центра проведена окружность, проходящая через точку C, пересекающая продолжения сторон AB и AD в точках E и F соответственно. Найти расстояние EF.
3) Имеется квадратный пруд, по углам которого растут 4 дуба. Пруд потребовалось увеличить, сохранив его квадратную форму, причём так, чтобы дубы оставались на своём месте, но не были бы затоплены, а стояли у берегов пруда. Как это нужно сделать?
4) Имеются песочные часы на 3 и 7 минут. Как с помощью этих часов можно отсчитать 4 минуты? 5 минут?
5) Барон Мюнхгаузен врёт по понедельникам, вторникам и средам, а в остальные дни говорит правду. В какой день недели он может заявить:
а) «Я врал вчера»; б) «Я буду врать завтра»; в) «Я врал вчера и буду врать завтра»?
6) Малыш может съесть торт за 10 минут, банку варенья – за 8 минут, выпить бидон чая за 15 минут. Карлсон может всё это сделать за 2, 3 и 4 минуты соответственно. За какое наименьшее время они могут вместе позавтракать банкой варенья, тортом и бидоном чая?
7) Решить в целых числах уравнение 2x = 8y + 1.