Мастер-класс. Сдай успешно ОГЭ!

Метапредметные

Личностные

Распознавать изученные геометрические фигуры, их элементы, пользоваться их свойствами при решении геометрических задач.
Решать задачи на вычисление длин отрезков и величин углов. Владеть понятием средней линии треугольника и трапеции, применять их свойства при решении геометрических задач. Проводить логические рассуждения с использованием геометрических теорем.
Решать задачи на клетчатой бумаге.
Проводить вычисления и находить числовые и буквенные значения углов в геометрических задачах с использованием суммы углов треугольников и многоугольников, свойств углов, образованных при пересечении двух параллельных прямых секущей. Решать практические задачи на нахождение углов.
Пользоваться теоремой Пифагора для решения геометрических и практических задач. Формулировать определения окружности и круга, хорды и диаметра окружности, пользоваться их свойствами. Уметь применять эти свойства при решении задач.
Владеть понятием описанной около треугольника окружности, уметь находить её центр. Владеть понятием касательной к окружности, пользоваться теоремой о перпендикулярности касательной и радиуса, проведённого к точке касания.
Владеть понятиями синуса, косинуса и тангенса острого угла прямоугольного треугольника. Пользоваться этими понятиями для решения практических задач.
Вычислять (различными способами) площадь треугольника и площади многоугольных фигур.
Выполнять арифметические действия с рациональными числами, сочетая устные и письменные приёмы, выполнять вычисления с иррациональными числами.
Находить значения степеней с целыми показателями и корней, вычислять значения числовых выражений.
Распознавать функции изученных видов. Показывать схематически расположение на координатной плоскости графиков функций вида:
y = kx, y = kx + b, y = k/x, y = ax2 + bx + c, y = x3, y = √x, y = |x|, в зависимости от значений коэффициентов, описывать свойства функций.

Познавательные УУД: выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа; выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях; предлагать критерии для выявления закономерностей и противоречий; проводить самостоятельно доказательства математических утверждений, выстраивать аргументацию, приводить примеры и контрпримеры; обосновывать собственные суждения и выводы; выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев).
Регулятивные УУД: владеть навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов; владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи; предвидеть трудности, которые могут возникнуть при решении задачи, вносить коррективы в деятельность на основе новых обстоятельств, данных, найденных ошибок, выявленных трудностей.
Коммуникативные УУД: представлять результаты решения задачи; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; участвовать в групповых формах работы, выполнять свою часть работы и координировать свои действия с другими членами команды; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы, обобщать мнения нескольких людей.

готовность и способность к математическому образованию и самообразованию на протяжении всей жизни;
готовность к активному участию в решении практических задач математической направленности;
эстетическое отношение к миру, включая эстетику математических закономерностей, объектов, задач, решений, рассуждений;
понимание математической науки как сферы человеческой деятельности, этапов её развития и значимости для развития цивилизации;
овладение языком математики и математической культурой как средством познания мира;
готовность осуществлять проектную и исследовательскую деятельность индивидуально и в группе.

Деятельность учителя

Деятельность обучающихся

Оргмомент и мотивация к деятельности

– Здравствуйте, уважаемые девятиклассники! Сегодня у нас не обычный урок, а урок - Мастер-класс от 11-классников. Перед вами сегодня выступят несколько ваших старших товарищей из 11-х классов…..
Они поделятся с вами своими знаниями и умениями и некоторым опытом, дадут вам советы, которые будут вам полезны для успешной  сдачи ОГЭ.
А ваша задача внимательно работать, задавать вопросы, и научиться самостоятельно верно решать задачи такого же вида.

Приветствуют учителя, выступающих ребят из 11 классов, настраиваются на работу.
Ведущие у доски с презентацией готовятся к выступлению.

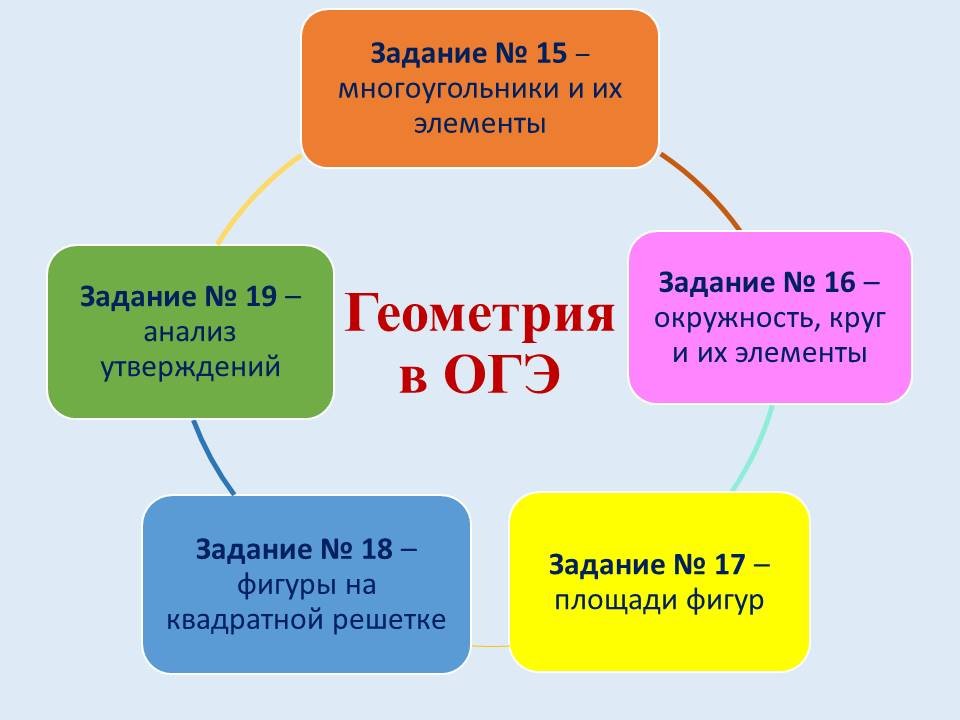
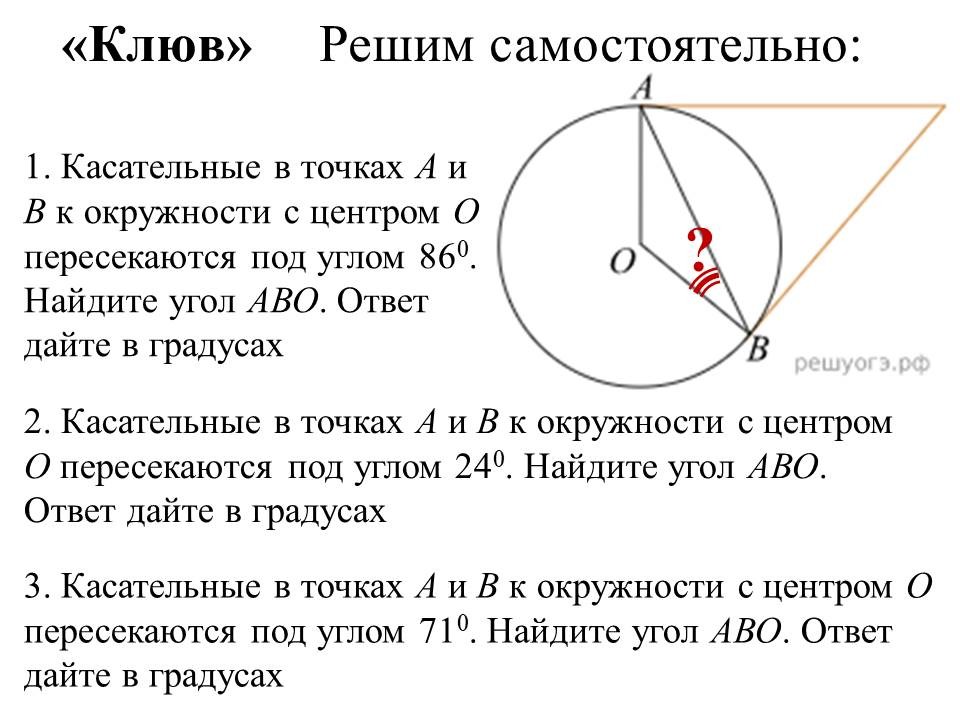
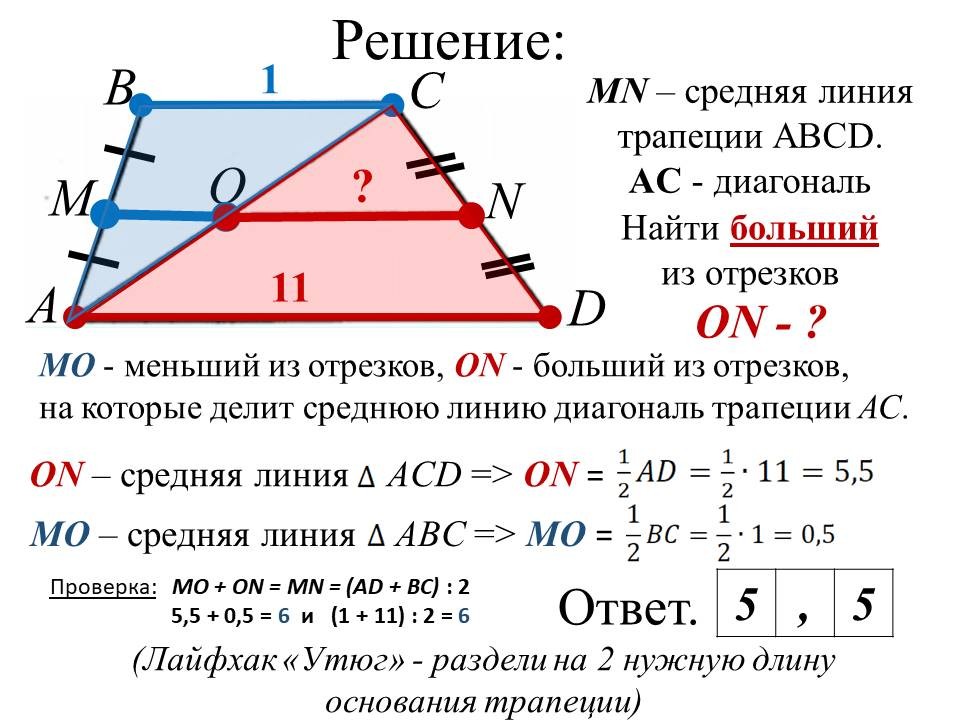
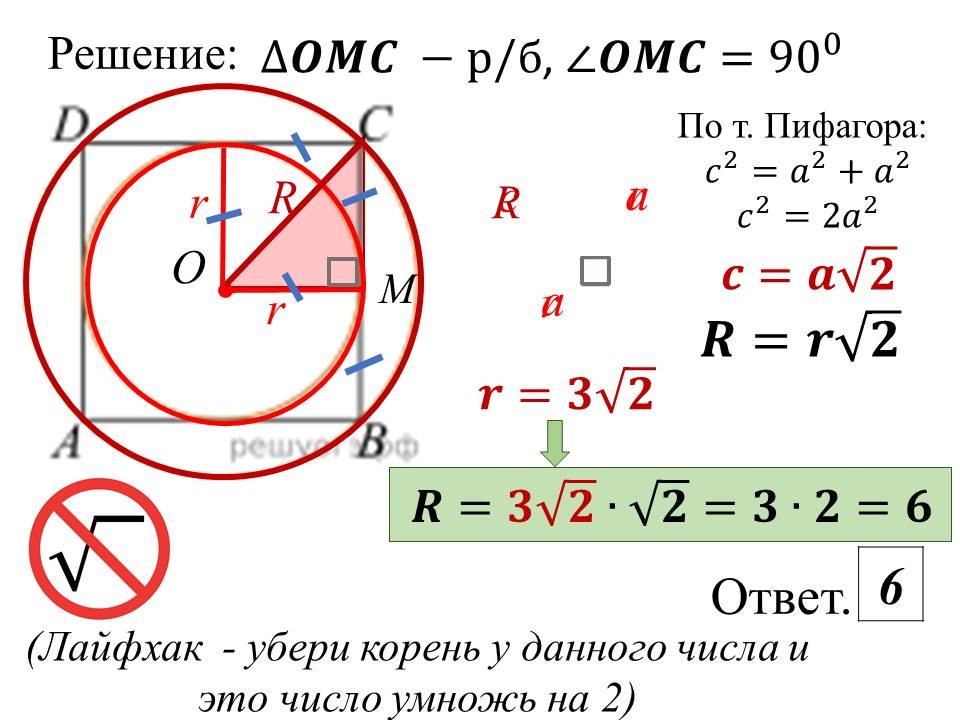
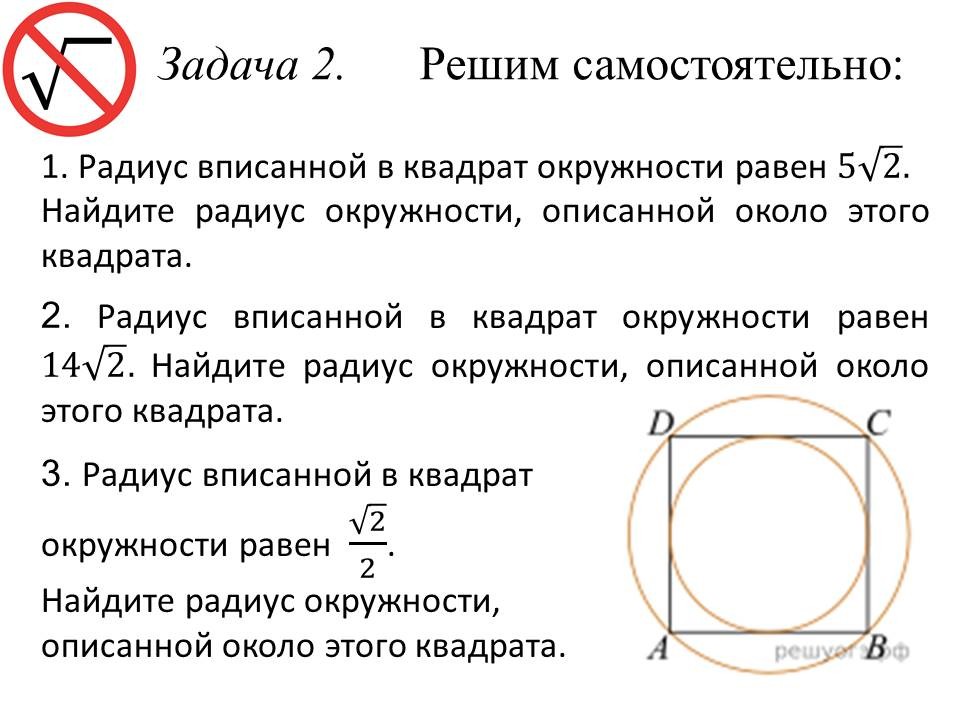
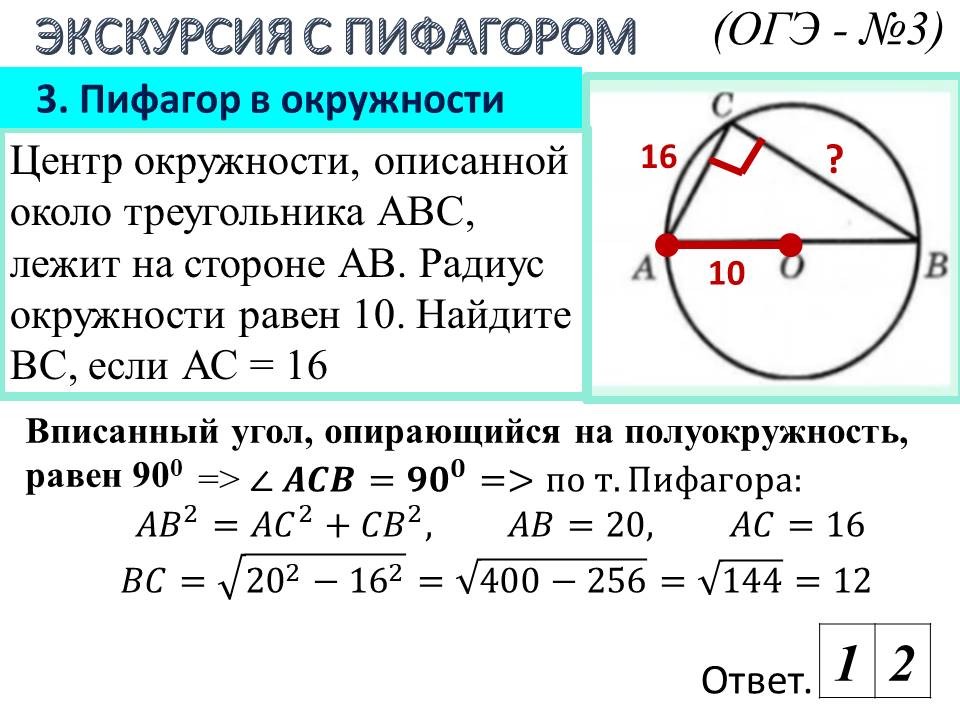
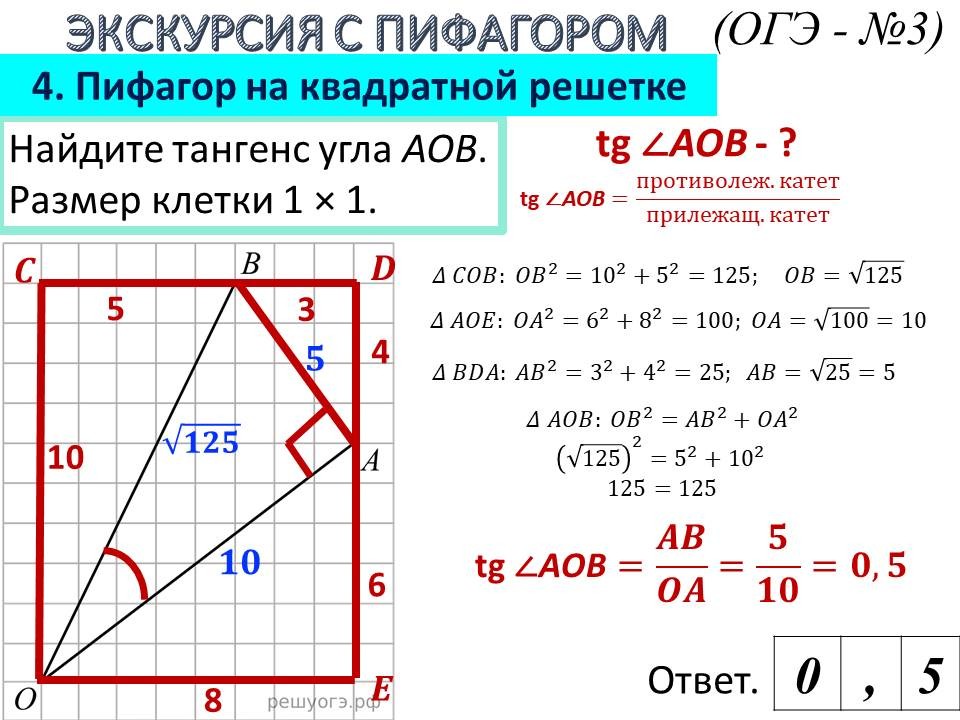
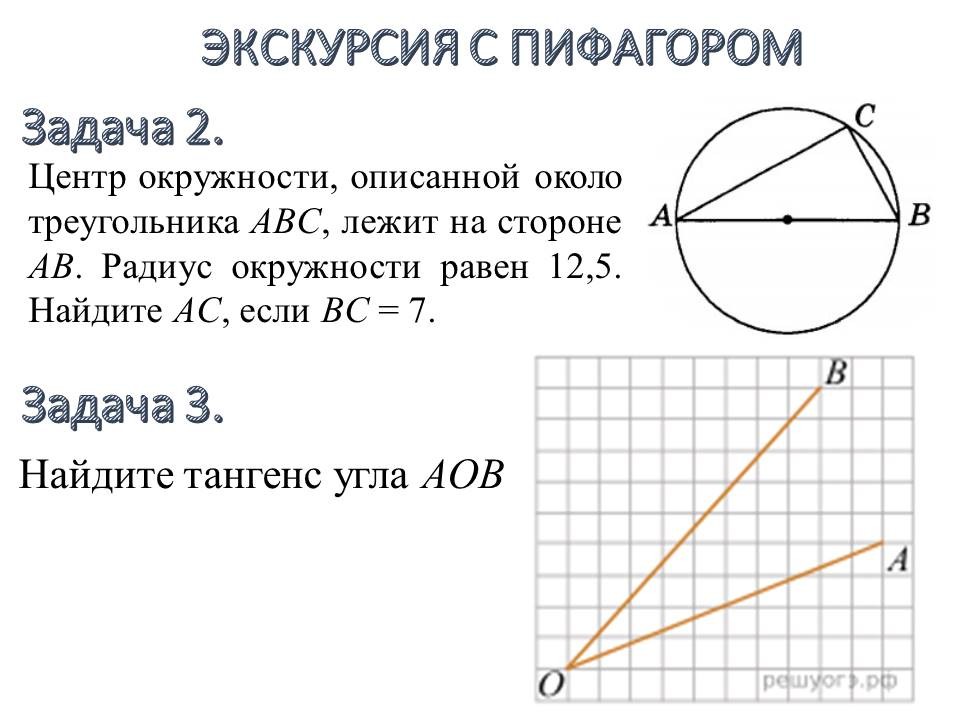
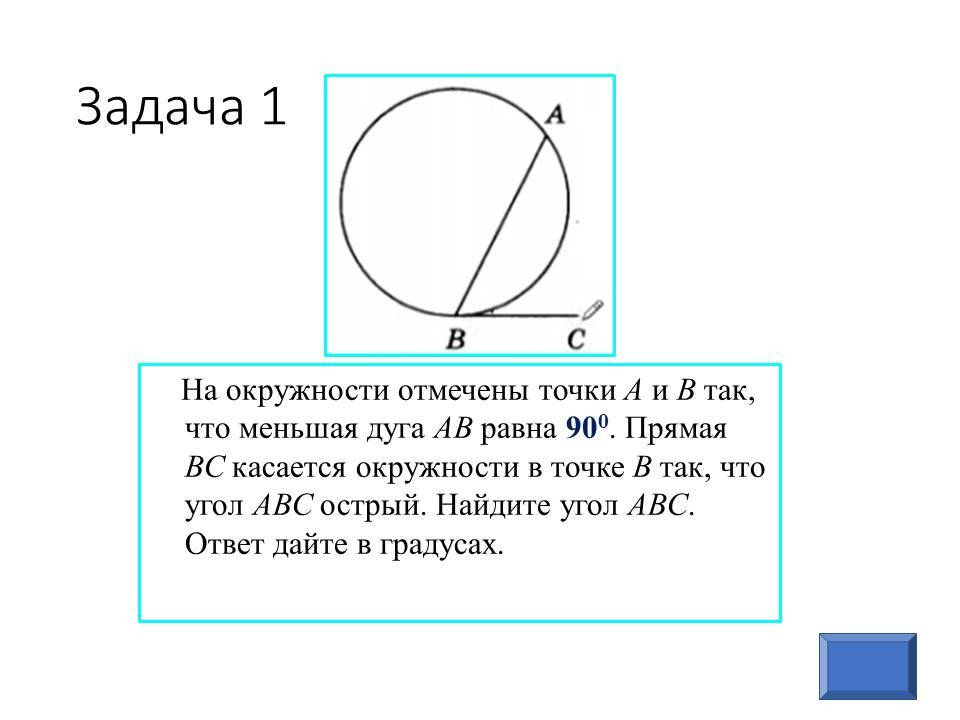
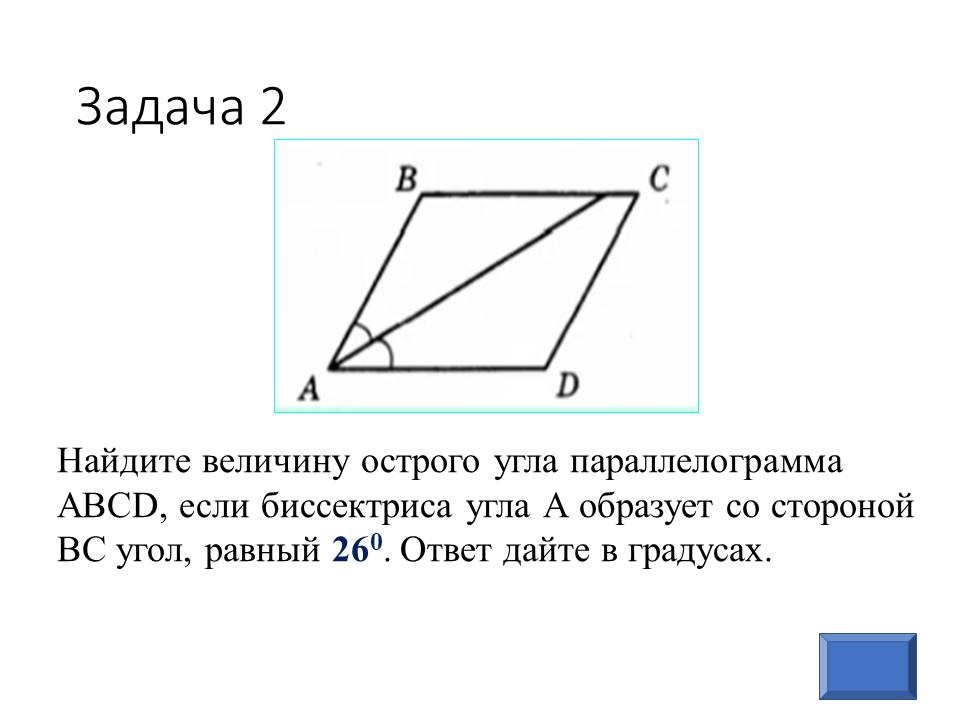
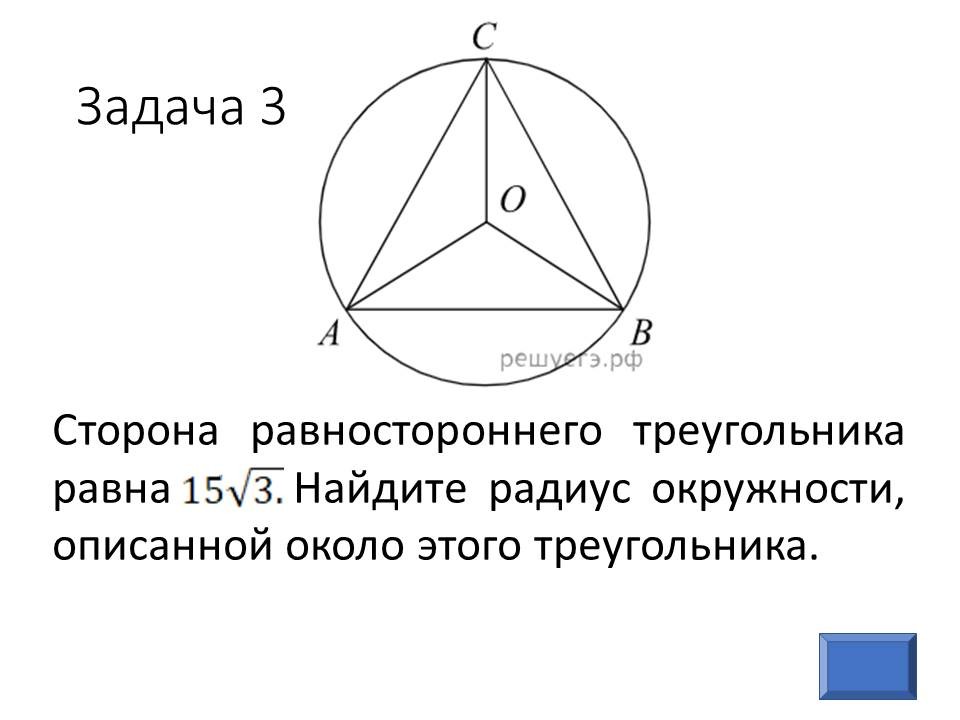
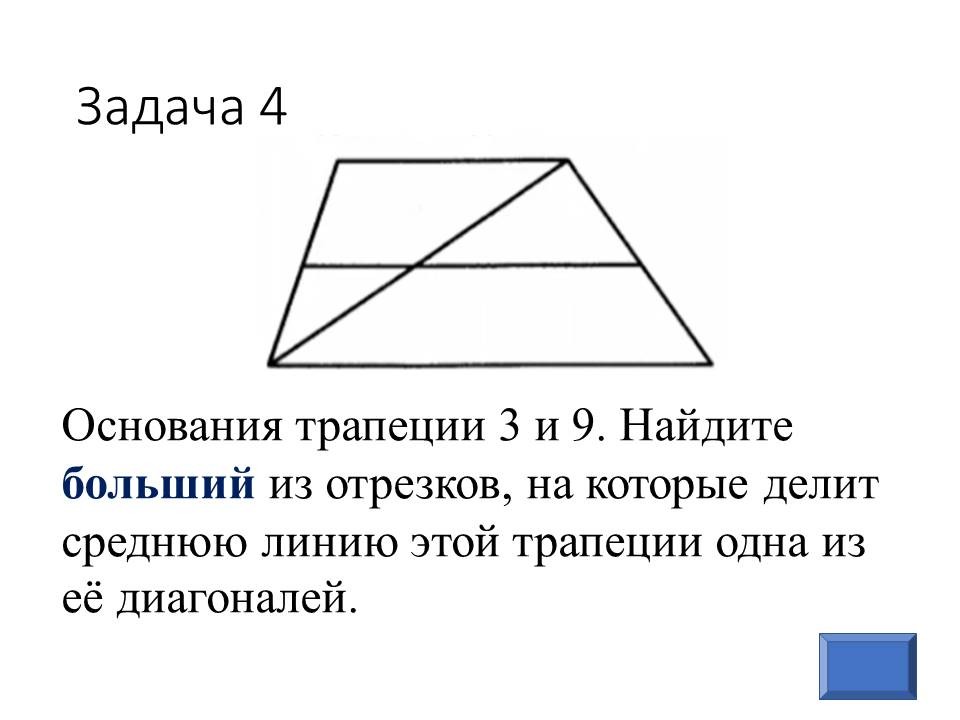
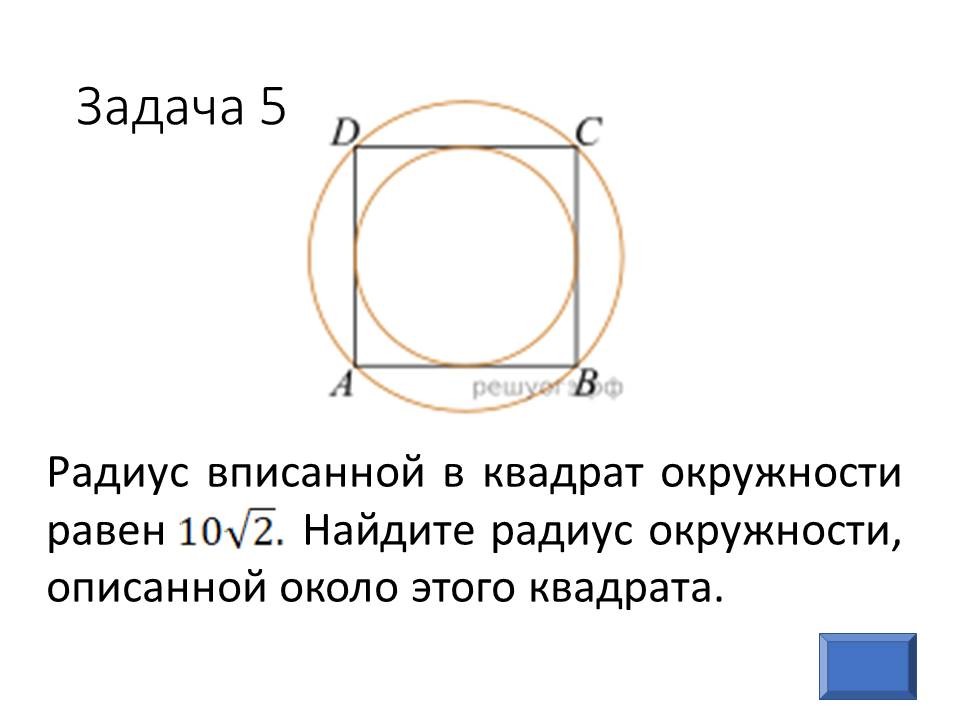
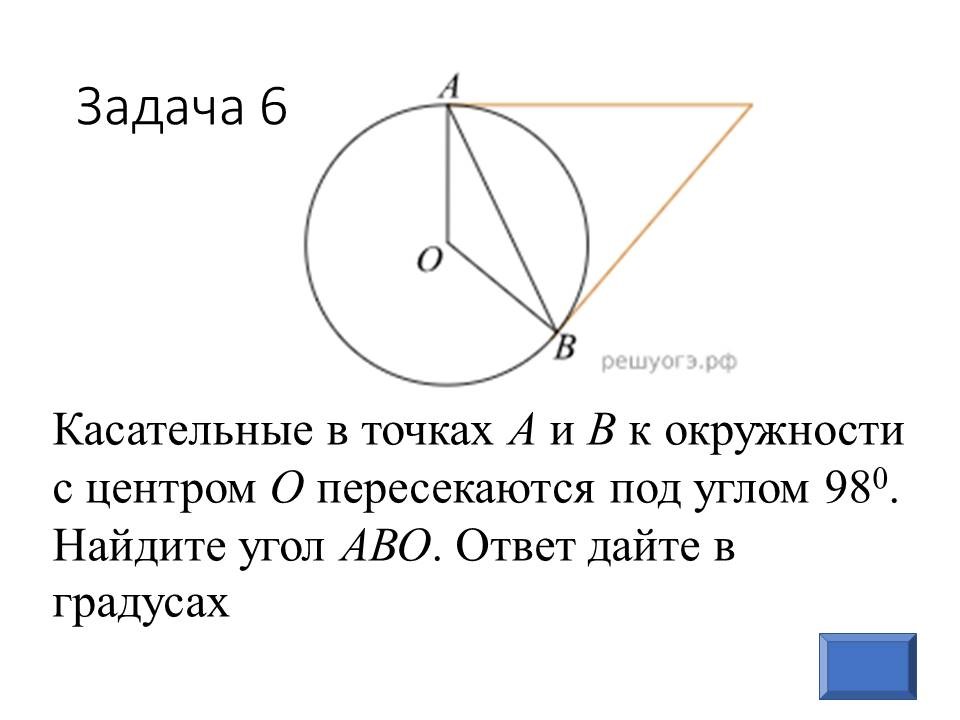
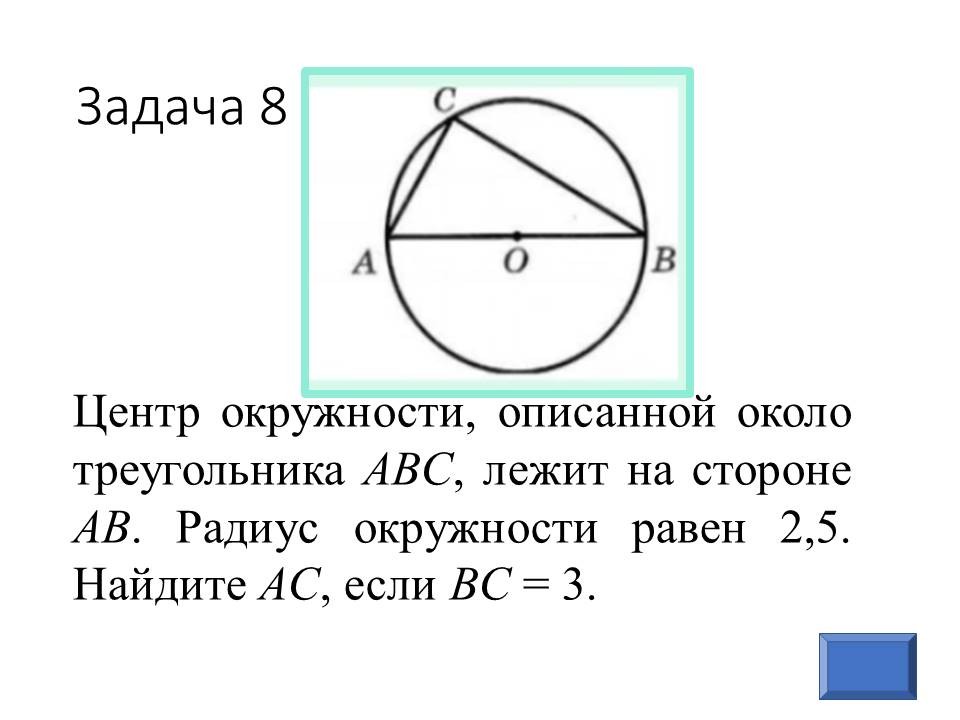
Геометрия в ОГЭ: лайфхаки для отдельных видов задач

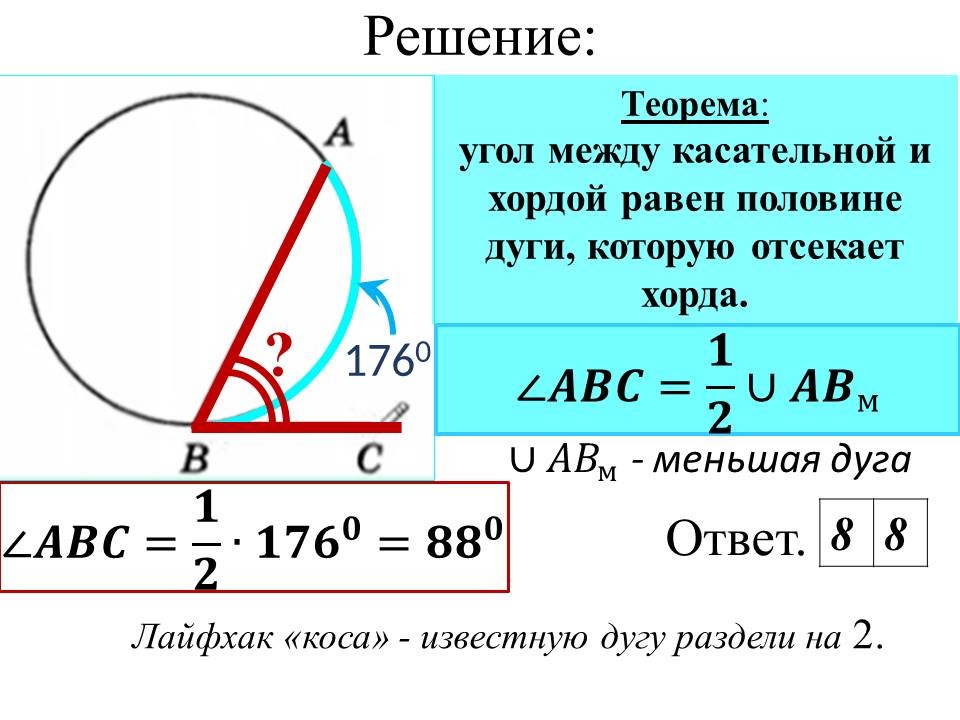
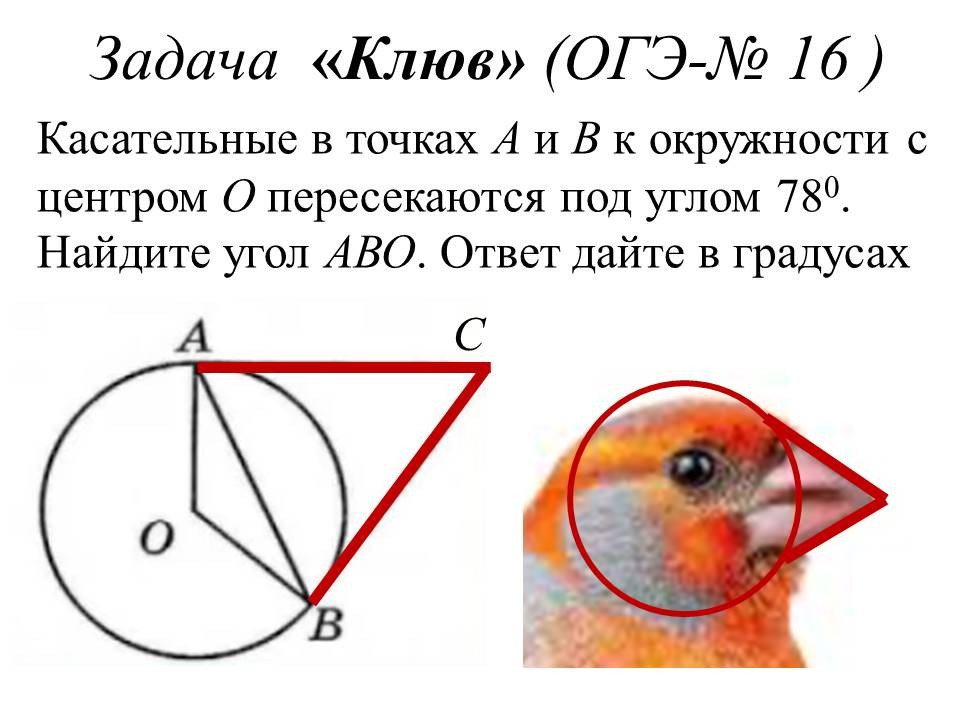
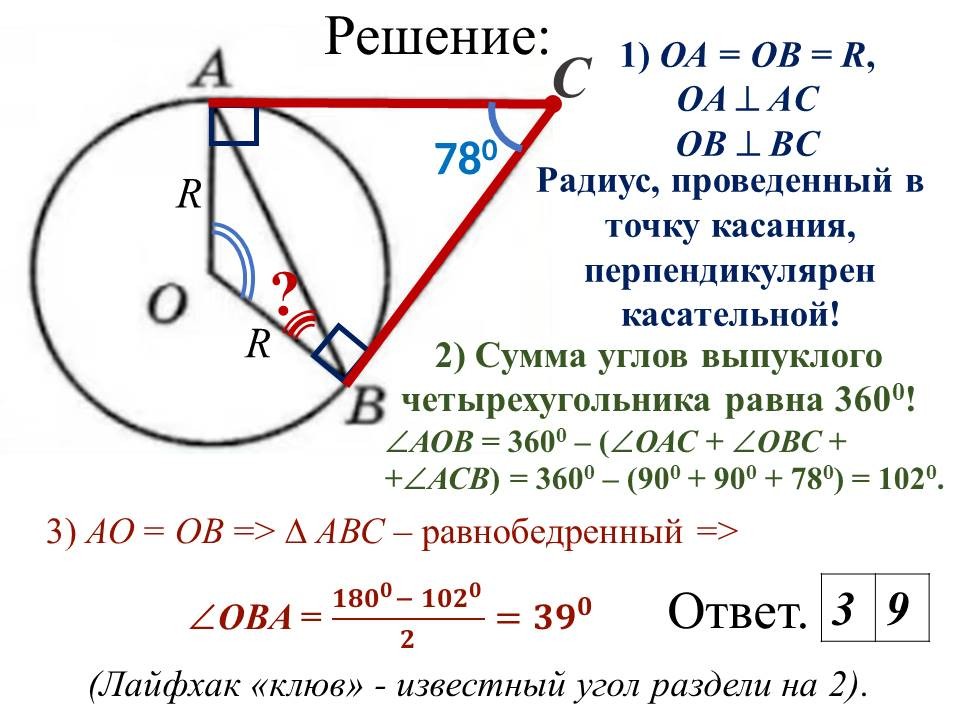
Ведущие 1 и 2 знакомят обучающихся 9 классов с некоторыми лайфхаками для отдельных задач геометрии, обосновывая способы решения изученными геометрическими фактами и теоремами. После ознакомления со способом решения, предлагают 9-классниками типичные задачи такого же вида для самостоятельного решения.

Прорабатывают способы решения, задают вопросы, решают самостоятельно, разбившись в команды по классам. Самые активные и верно выполнявшие задания обучающиеся из 9 классов награждаются в конце урока.

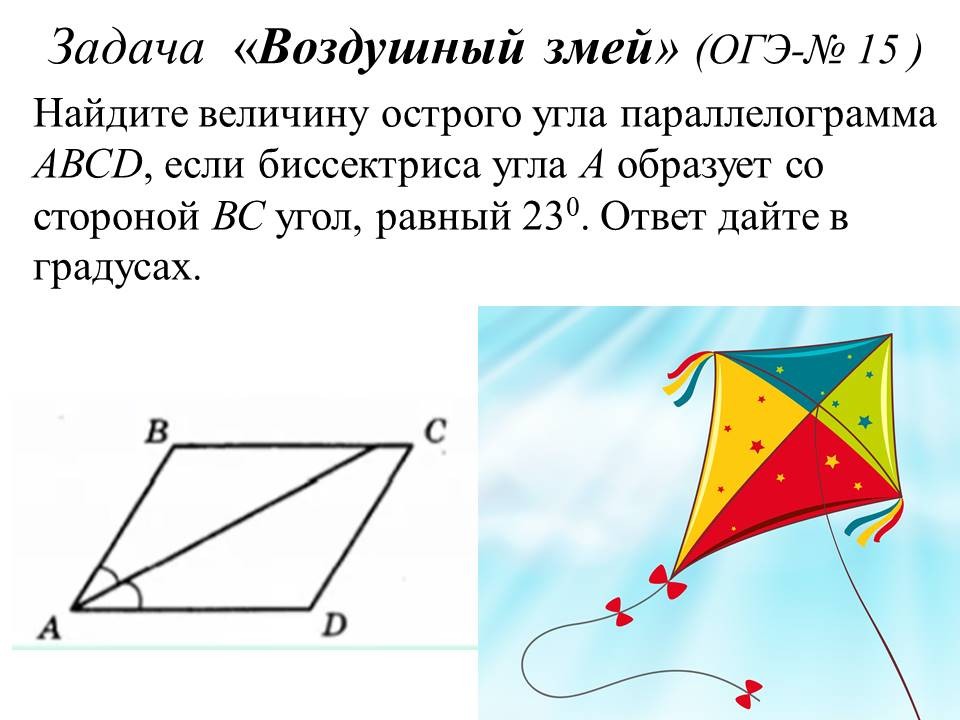
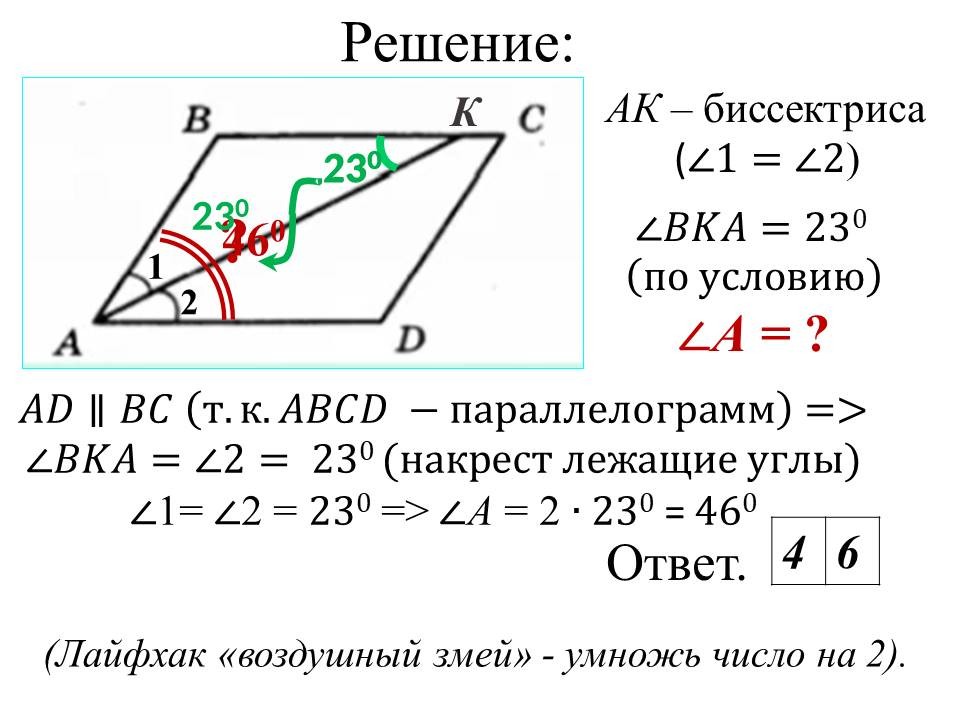
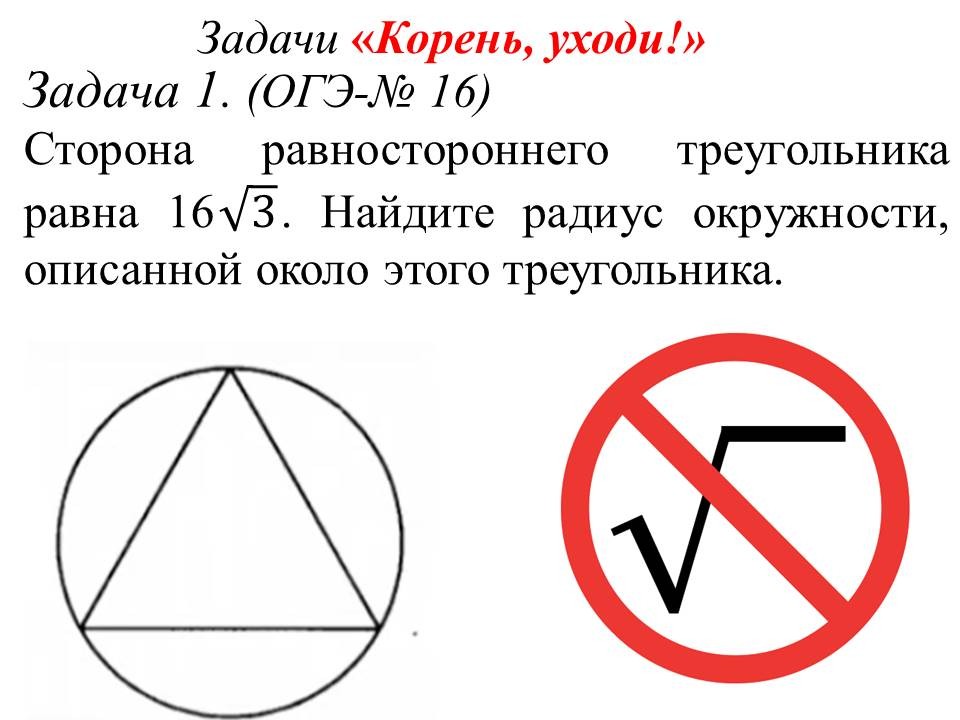
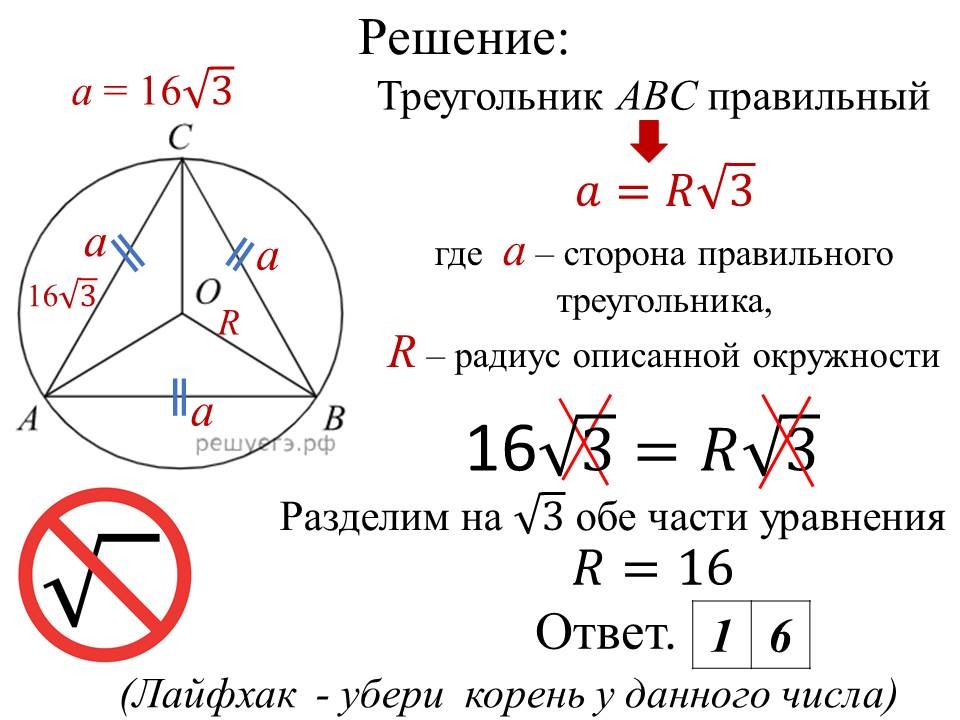
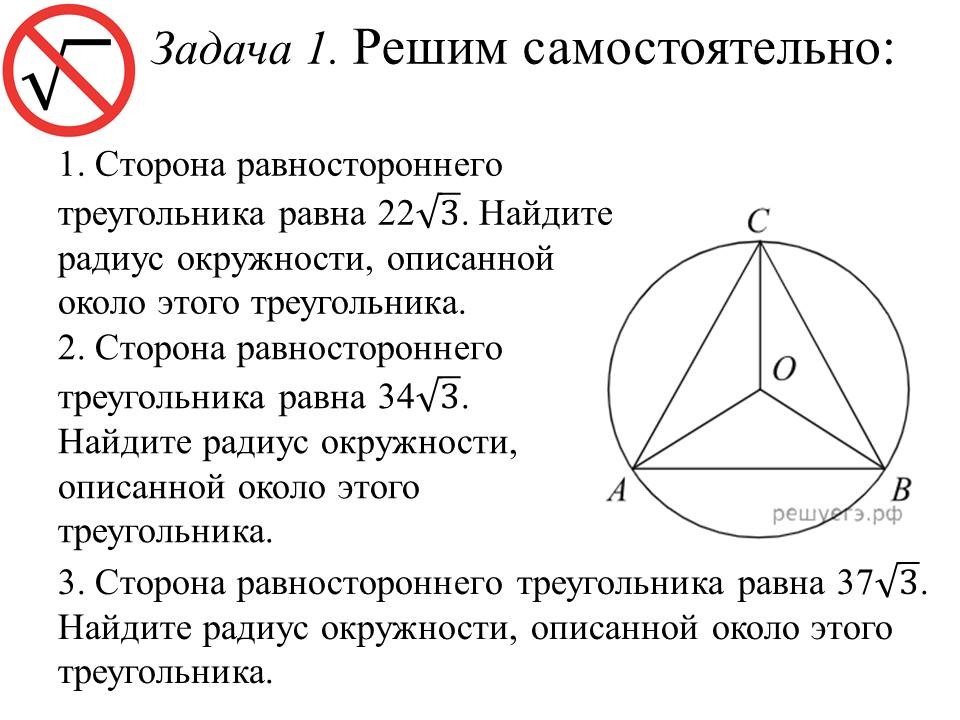
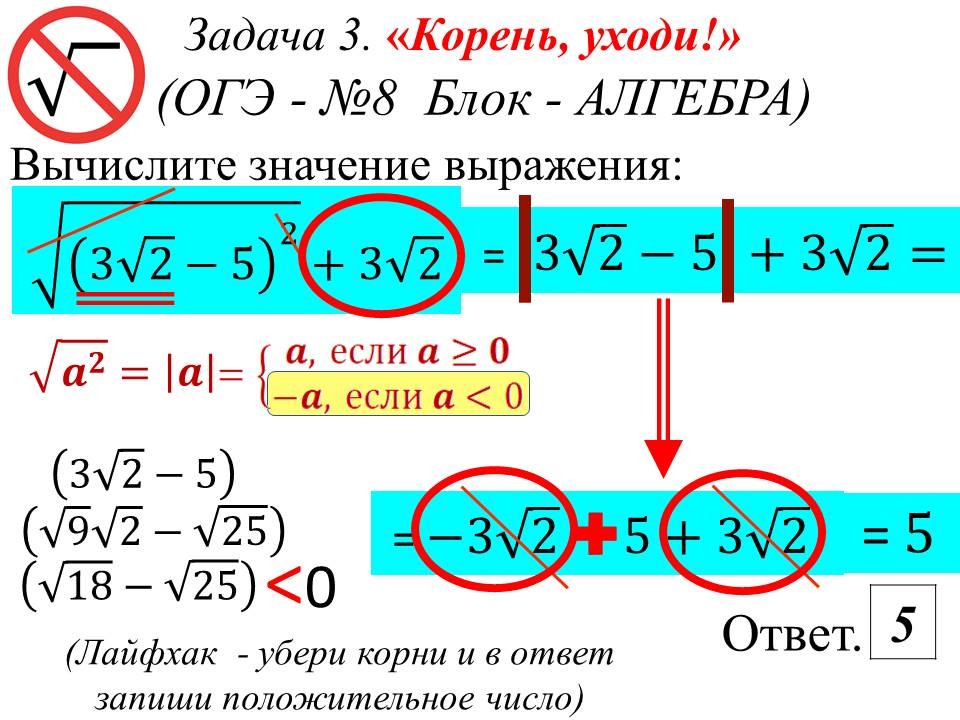
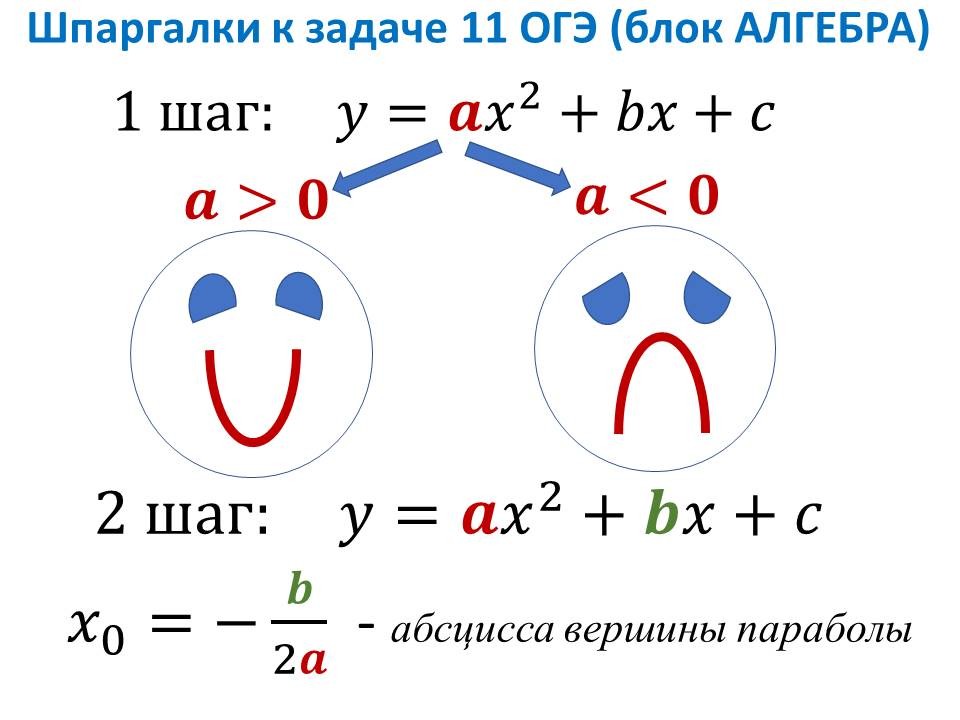
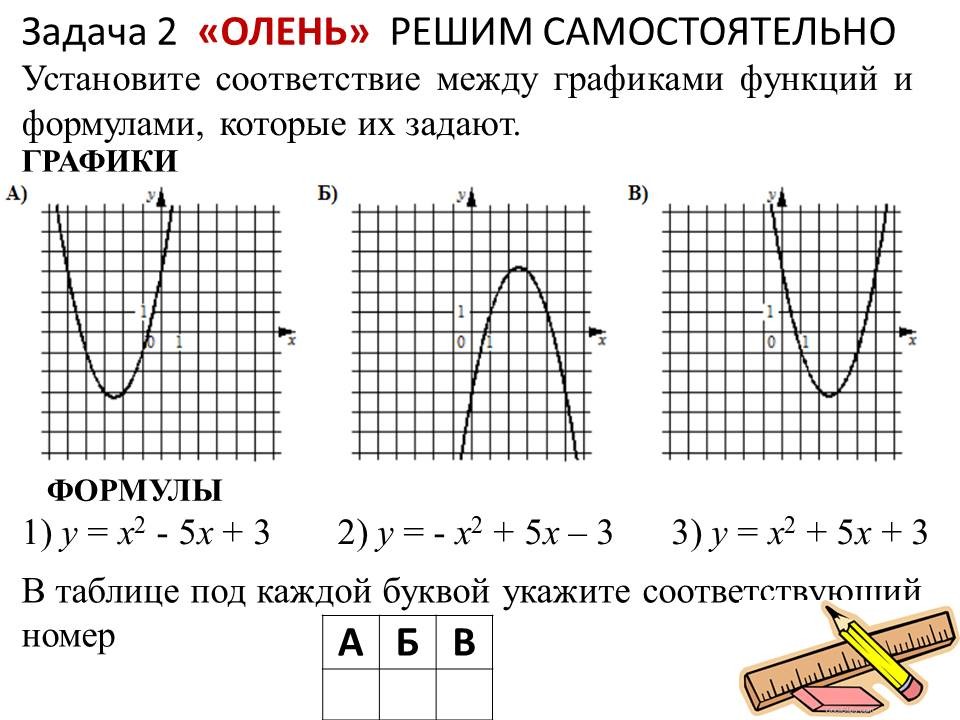
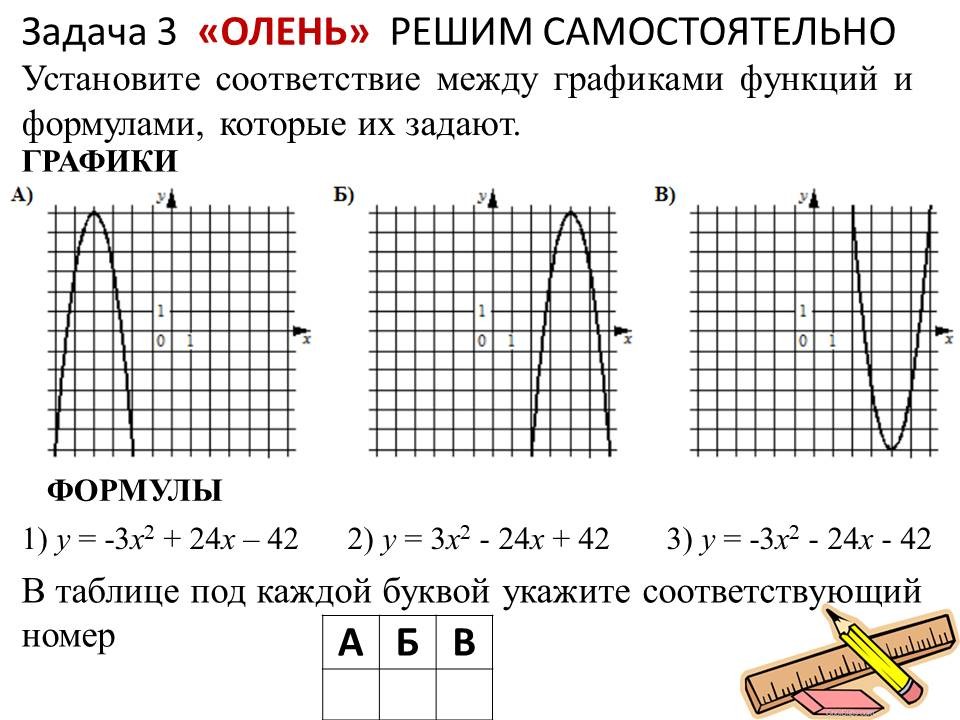
Решение алгебраических задач ОГЭ: легкие способы решений сложных заданий

Ведущие 3 и 4 знакомят обучающихся 9 классов с некоторыми лайфхаками для отдельных задач алгебры. После ознакомления со способом решения, предлагают 9-классникам типичные задачи такого же вида для самостоятельного решения.

Прорабатывают способы решения, задают вопросы, решают самостоятельно, разбившись в команды по классам. Самые активные и верно выполнявшие задания обучающиеся из 9 классов награждаются в конце урока.

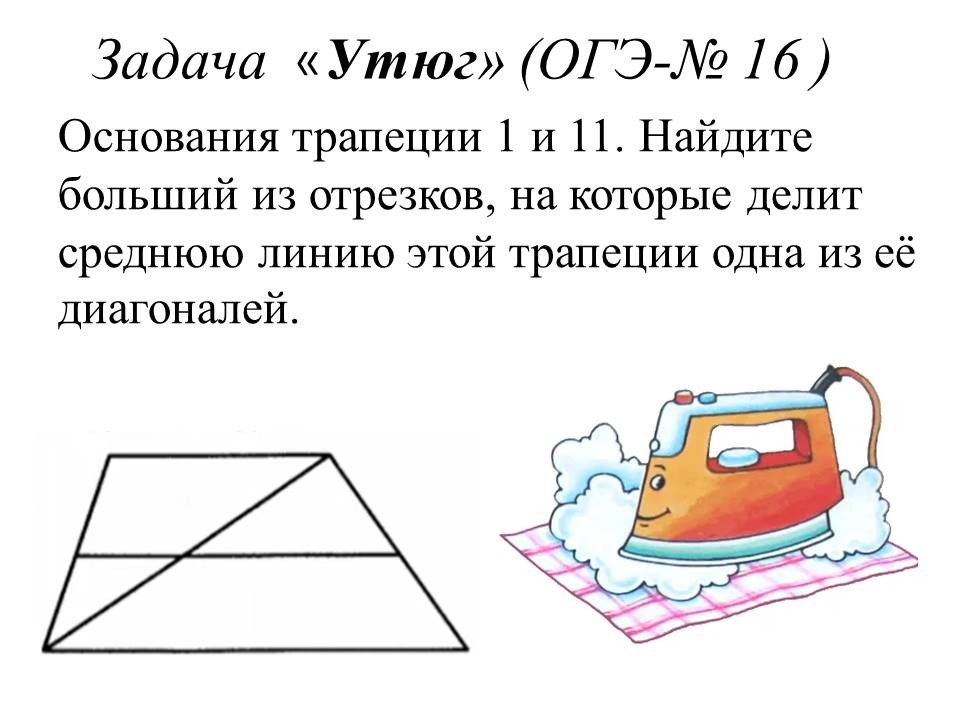
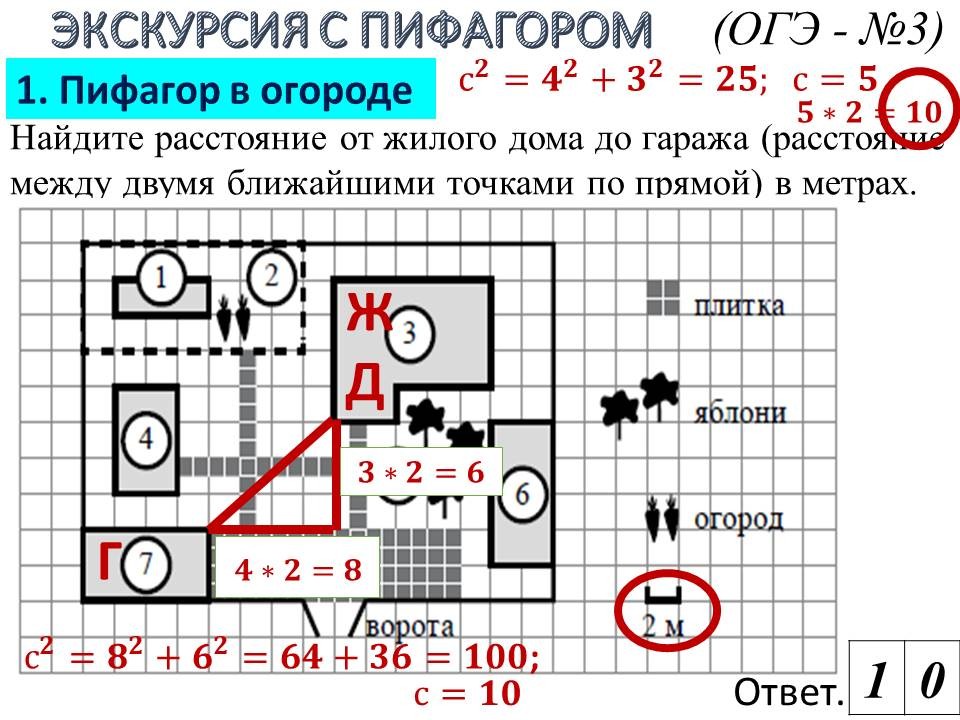
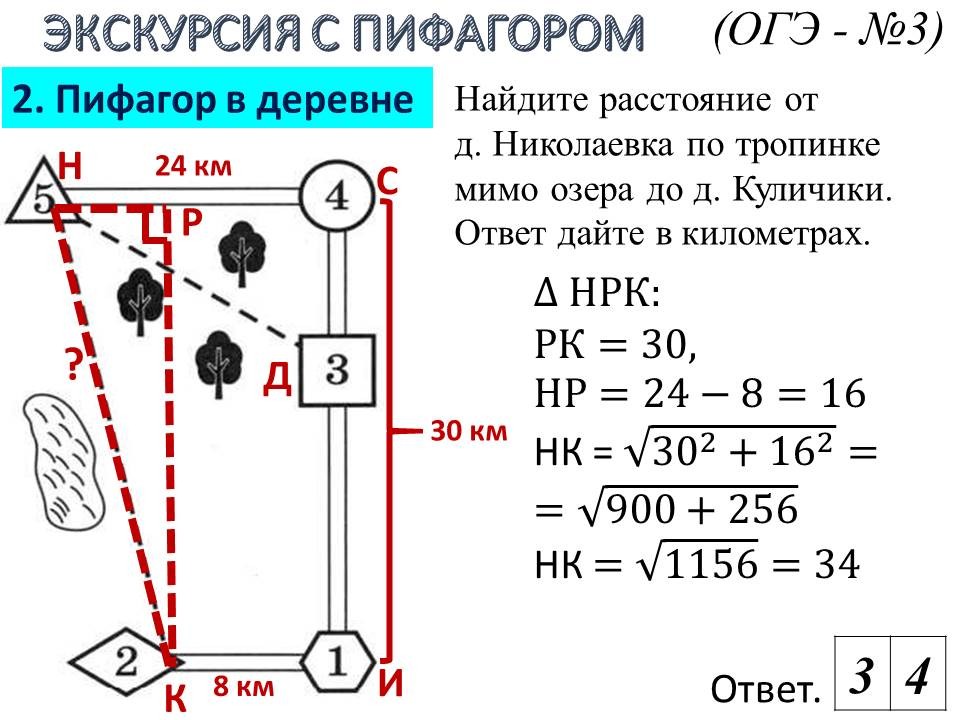
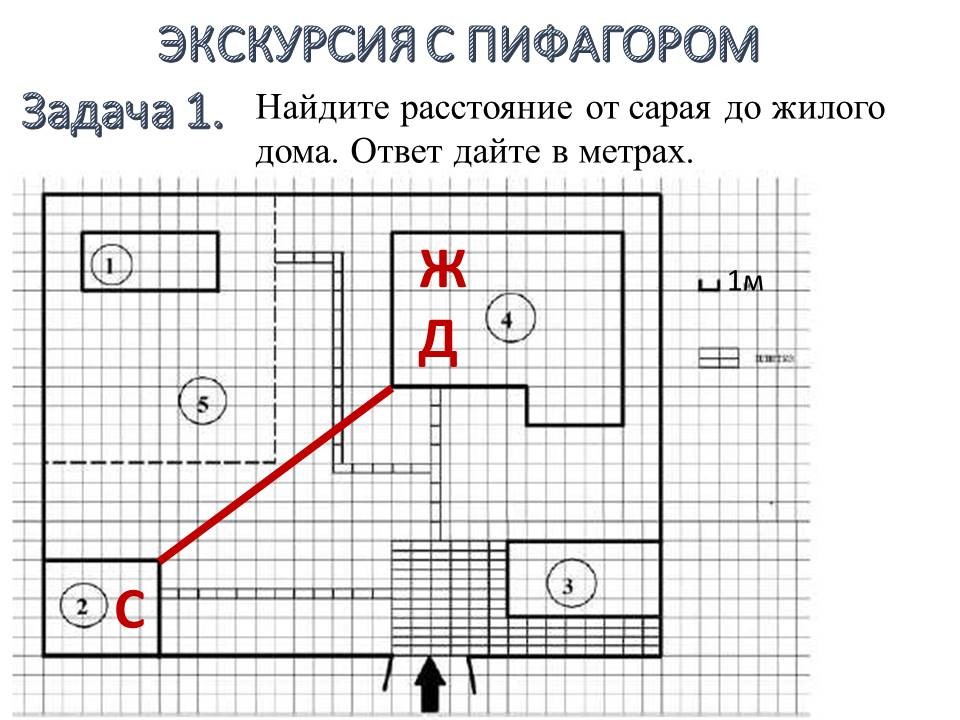
Решение практических задач ОГЭ №1-5: некоторые лайфхаки

Ведущие 5 и 6 знакомят обучающихся 9 классов с некоторыми лайфхаками для отдельных практических задач 1-5. После ознакомления со способом решения, предлагают 9-классниками типичные задачи такого же вида для самостоятельного решения.

Прорабатывают способы решения, задают вопросы, решают самостоятельно, разбившись в команды по классам. Самые активные и верно выполнявшие задания обучающиеся из 9 классов награждаются в конце урока.

Экспресс-тест ОГЭ

- А сейчас мы проведем экспресс-тест ОГЭ, чтобы быстро определить, какие задачи из рассмотренных сегодня на уроке вы научились решать, а какие еще требуют дополнительной проработки. Перед вами на слайде 9 цифр – это номера задач, которые сейчас вам нужно решить, ответы на них вы записываете в бланк у вас на столе.

Решают задачи, вписывают ответы в бланк, передают жюри по окончании решения.

Подведение итогов Рефлексия

- Пока жюри подсчитывает результаты и подводит итоги,  просим вас выразить свое мнение об этом уроке, о своей работе на уроке и о работе наших старших ребят, выступавших сегодня для вас. В карточках у вас на столе закончите предложения и обведите один из смайликов.
Ведущие цитируют великих ученых:
Айвен Нивен: «Математику нельзя изучать, наблюдая, как это делает сосед!»
Дьёрдь Пойа: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их».
Подведение итогов, объявление благодарности выступившим 11-классникам, объявление победителя среди 9-классников, активно работающих на уроке, награждение.

Выражают свое мнение о своей работе на уроке, понравился ли им урок:
«Закончите предложение»
1. Сегодня на уроке мне было сложно…
2. Сегодня на уроке мне было легко…
3. Сегодня на уроке мне понравилось…
4. Мне более всего понравилось выступление ведущего …., потому что…..

 
Получение награждений и благодарностей.