Значение логического выражения. Методика преподавания темы на уроках в 8–9-х классах и для подготовки к ОГЭ
Скачать презентацию (505.08 КБ)
Скачать презентацию (671.89 КБ)
Для максимально быстрого и однозначно верного решения задач будем придерживаться принципа: чем меньше вычислений и другой работы мы делаем, тем меньше времени потрачено на решение и тем меньше вероятность появления ошибок в результате.
Для более наглядного отображения логических отношений между множествами точек А и В будем использовать геометрическую схему в виде кругов Эйлера (рис.1).
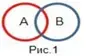
Точка принадлежит множеству А, если она находится внутри круга, его ограничивающего, что записывается в виде А=1 (истина), иначе А=0 (ложь).
Правил при получении результатов выполнения логических операций много, а исключения всего два, поэтому и будем решать задачи именно через исключения.
Результатом применения логических операций могут быть только истина (1) или ложь (0).
Существуют всего три базовые логические операции, при помощи которых строятся логические выражения:
НЕ, И и ИЛИ:
НЕ: инверсия (отрицание). Обозначается знаком , например, А). Результат применения: 1 = 0, 0 = 1, т.е. истина превращается в ложь, а ложь - в истину. Будем говорить, что операция НЕ ( ) переворачивает результат (значение);
И: конъюнкция (логическое умножение). Обозначается знаками ˄ либо & (например, А ˄ В либо А & В). Результатом выполнения конъюнкции служит пересечение множеств А и В (на рис.2 выделено жёлтым цветом).
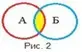
При этом точка принадлежит пересечению множеств А и В, если она принадлежит одновременно обоим множествам:
А & B = 1 при А=1 и В=1.
Во всех остальных случаях в результате применения выражения И получаем ложь.
Таким образом, исключение № 1:
«И» правда, когда все части выражения правда;
ИЛИ: дизъюнкция (логическое сложение). Обозначается ˅ (например, А ˅ В). Результатом выполнения дизъюнкции служит объединение множеств А и В (на рис.3 выделено зеленым цветом).
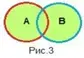
При этом точка не принадлежит объединению множеств А и В, если она не принадлежит ни А, ни В:
А ˅ B = 0 при А=0 и В=0.
Во всех остальных случаях в результате применения выражения ИЛИ получаем правду.
Таким образом, исключение № 2:
«ИЛИ» ложно, когда все части выражения ложны.
При вычислении логических выражений следует помнить, что логические операции выполняются в следующем порядке: НЕ, И, ИЛИ. Как и в математике, скобки могут поменять последовательность их выполнения.
При этом любая операция, которая выполняется последней, может поменять результат, а операция НЕ, стоящая перед скобками, переворачивает результат, полученный в скобках.
Желающим решать задачи, открывая скобки в выражениях, необходимо знать законы алгебры логики!
Законы рефлексивности:
a ∧ a = a, то есть 0*0 =0 или 1*1 = 1
a ∨ a = a, то есть 0+0=0 или 1+1 = 1
Законы коммутативности:
a ∧ b = b ∧ a, то есть a*b = b*a
a ∨ b = b ∨ a, то есть b+b = b+a
Законы ассоциативности:
(a ∧ b) ∧ c = a ∧ (b ∧ c), то есть (a*b) * c = 1 при a=b=c=1 или равно 0 в противном случае
(a ∨ b) ∨ c = a ∨ (b ∨ c), то есть (a + b) + c = 0 при a=b=c=0 или равно 1 в противном случае
Законы дистрибутивности:
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c), то есть a*(b + c) = (a*b) + (a*c), то есть 0*(b V c) = 0 или 1*(b V c) = b V c
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) , то есть a+(b*c) = (a+b) * (a+c), то есть (1+b)*(1+c) = 1 или 0+(b*c) = b*c
Закон отрицания отрицания:
( a) = a, то есть -(-a) = a
Законы поглощения:
a ∧ (a ∨ b) = a, то есть a*(a + b) равно 0 при а=0 или 1 - в обратном случае.
a ∨ (a ∧ b) = a, то есть a+(a*b) равно 1 при а=1 или 0 - в обратном случае.
Законы де Моргана:
(a ∧ b) = a ∨ b, то есть 0 при a=b=1 и =1 - в обратном случае.
(a ∨ b) = a ∧ b, то есть -(1) = 0 или -(0) = 1, то есть = 0 при а=1 или b=1 и 1 - в обратном случае.
Другими словами:
Если перед скобкой стоит знак НЕ, то при открытии скобок следует менять на противоположные все знаки, стоящие перед логическими выражениями ("+" на "-" и наоборот) и логические операции ("И" на "ИЛИ" и наоборот):
(А & В) = ( А) V ( В), то есть НЕ (А И В) = (НЕ А) ИЛИ (НЕ В)
( А V В) = ( А) & ( В), то есть НЕ (А ИЛИ В) = (НЕ А) И (НЕ В)
Например,
НЕ ((Первая буква гласная) И (Последняя буква согласная)) =
=НЕ (Первая буква гласная) ИЛИ НЕ (Последняя буква согласная)
При открытии скобок с математическими сравнениями внутри следует помнить, что знаков сравнения всего три: > (больше), < (меньше) и = (равно), и при открытии скобок с отрицанием перед ними следует менять эти знаки на противоположные, то есть:
НЕ (>) заменяется на (<=)
НЕ (<) заменяется на (>=)
НЕ (=) заменяется на два знака (<>)
или наоборот:
НЕ (≥ или >=) заменяется на (<)
НЕ (≤ или <=) заменяется на (>)
НЕ (<>) заменяется на (=).
Главное здесь - не забывать про строгое равенство - знак «=»!