Реализация принципа наглядности на уроках математики через приемы мнемотехники
Образование играет важнейшую роль в жизни каждого человека. Одним из ярких представителей отечественной педагогики является Константин Дмитриевич Ушинский, чье наследие продолжает жить и развиваться в современном образовании.
Константин Дмитриевич Ушинский был выдающимся педагогом XIX века, чьи идеи и методы обучения до сих пор оказывают влияние на современное образование в России и за её пределами.
Современное образование тесно связано с идеями К.Д.Ушинского, и многие из его принципов и методов продолжают быть актуальными в наше время.
Индивидуализация обучения, внедрение новых технологий, активное использование наглядных пособий и методов формирования моральных и духовных качеств учеников - все это стало неотъемлемой частью образовательного процесса. В настоящее время многие педагоги и ученые продолжают развивать идеи Ушинского, применяя их на практике и адаптируя к современным условиям. Одним из ярких примеров является концепция "личностно-ориентированного образования", которая базируется на идеях Ушинского об индивидуализации и развитии личности ученика.
«Необходимыми условиями» всякого преподавания Ушинский считал:
- своевременность;
- постепенность;
- органичность;
- постоянство;
- твердость усвоения;
- ясность;
- самодеятельность учащихся;
- отсутствие чрезмерной напряженности и чрезмерной легкости;
- нравственность;
- полезность.
Анализ содержания каждого из них ясно показывает, что под «нравственностью» Ушинский понимал воспитывающий характер обучения, под «полезностью» связь обучения с жизнью, под «своевременностью» и «органичностью» природосообразность в обучении, а под остальными «условиями» то, что мы называем дидактическими принципами обучения.
В результате изучения теории обучения Ушинского в целом, можно сделать вывод, что основными дидактическими принципами обучения Ушинский считал:
- сознательность и активность учащихся в процессе обучения («ясность», «самодеятельность учащихся»;
- наглядность в обучении;
- последовательность («постепенность», «отсутствие чрезмерной напряженности и чрезмерной легкости»);
- прочность знаний и навыков (твердость усвоения).
Исключительно большое значение К.Д.Ушинский придавал принципу наглядности в осуществлении одной из важнейших задач обучения - сделать учение основательным и вместе с тем как можно более легким.
Он пишет: «Кто не замечал над собою, что в памяти нашей сохраняются с особенной прочностью те образы, которые мы воспринимаем сами посредством созерцания, и что к такой, врезавшейся в нас, картине, мы легко и прочно привязываем даже отвлеченные идеи, которые без того изгладились бы быстро.
Ушинский большое значение придавал наглядности обучения и наглядным пособиям для внедрения в детях навыка самостоятельного, последовательного изложения своих мыслей.
Мнемотехника
«Учите ребёнка каким-нибудь неизвестным ему пяти словам - он будет долго и напрасно мучиться, но свяжите двадцать таких слов с картинками, и он усвоит на лету»
К.Д.Ушинский
В этом и состоит суть мнемотехники - системы методов и приёмов, обеспечивающих эффективное запоминание, сохранение и воспроизведение информации.
При изучении математики нужно знать определения, правила, формулы, алгоритмы решения, графики, значения некоторых величин и т.д. Как помочь детям запомнить? Как достичь стойкого запоминания?
Чтобы хорошо запомнить определение, формулу, значение, лучше установить ассоциацию с каким-то уже известным фактом с помощью воображения. (Ассоциация это мысленная связь между двумя образами).
Чтобы облегчить детям запоминание математических формул и правил я в своей работе использую мнемотехнику.
Мнемотехника - совокупность специальных приемов и способов, облегчающих запоминание информации и увеличивающих объем памяти путем образования ассоциаций.
Задачи:
- Изучить приёмы мнемотехники.
- Показать необходимость использования мнемотехники в старшей школе.
- Собрать коллекцию мнемотехник, для школьников и учителей.
Актуальность
Для многих учащихся, запомнить и заучить формулы и правила наизусть трудно. Система образов помогает понять и воспроизвести научную информацию. Применение мнемотехники дает возможность переключения, своеобразного отвлечения от науки на уровень житейских ассоциаций, игры, воображения и фантазии.
Школа - это огромное поле деятельности для применения мнемотехники. На уроках математики приемы мнемотехники можно использовать очень продуктивно. Ребята очень хорошо запоминают правило ассоциируя его с чем-то. Приёмы мнемотехники активно используют в начальной школе, в 5-6 классе. В старших классах учителя забывают про такую форму работы, но в старшей школе намного больше теории, поэтому нужно использовать мнемотехнику и у старшеклассников. Подростки быстрее и легче вспоминают мнемотехники, чем припоминают правила.
Среди основных мнемонических методов и приемов можно выделить следующие:
- Ассоциации. Нахождение ярких необычных ассоциаций, которые соединяются с запоминаемой информацией.
- Рифмы. Создание рифмованных фраз и стихотворений, содержащих запоминаемый материал.
- Созвучие. Запоминание терминов с помощью созвучных известных слов или словосочетаний
- Ключевые слова. Выделение в каждой фразе одного - двух ключевых слова, припомнив которые немедленно вспоминаешь целиком и всю фразу.
Помните, что такое биссектриса угла? «Биссектриса - это крыса, которая бегает по углам и делит их пополам». А порядок следования цветов в радуге? «Каждый охотник желает знать, где сидит фазан». Все помнят, и это подтверждение тому, что приемы мнемоники работают!
Общие законы запоминания:
- использовать ключевые слова, схемы, таблицы;
- чем интереснее, тем легче запомнить;
- чем ярче впечатление от созданного образа, тем прочнее запоминание.
Примеры применения мнемотехник на уроках математики
1. Приведение подобных слагаемых
8х + 2у + 6х - 10у.
«яблоки» складываем с «яблоками», «бананы» - с «бананами».
2. Запись смешанного числа неправильной дробью
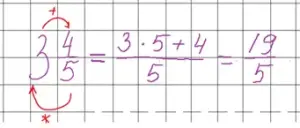
При изучении правила как записать смешанную дробь неправильной ребята легко запоминают этот стишок, вместо правила.
Снизу вверх я умножаю,
И числитель прибавляю,
Знаменатель оставляю.
3. Распределительный закон умножения
При изучении распределительного свойства умножения можно использовать ассоциацию «Фонтанчик»:
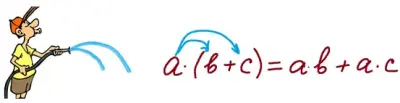
4. Решение уравнений
При решении уравнений учащиеся имеют проблемы со знаками при переносе слагаемых.
3х+5=2х-10
Проговариваем правило так:
Знак равенства - это река. При переходе через реку с одного берега на другой, одежда у слагаемых намокает, значит надо ее сменить, то есть поменять знак.
5. Сложение положительных и отрицательных чисел
В этой теме два правила - сложение чисел с одинаковым знаком и сложение чисел с разными знаками. Обучающиеся как правило испытывают трудности в их применении.
Рассказываю сказку: две армии - армия отрицательных и армия положительных чисел. При встрече солдат одной армии, они объединяются под своим флагом. При встрече солдат разных армий, начинается битва. Победит та армия, представителей которой больше. «Оставшиеся в живых» поднимают свой флаг.

6. Построение точки на плоскости
При построении точки на координатной плоскости ,следует придерживаться такого правила: первоначально заходим в подъезд, а затем поднимаемся на этаж (х - подъезд; у - этаж).
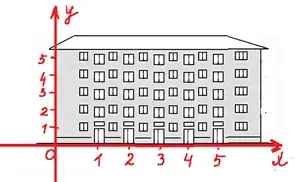
7. Решение неравенств
Чтобы правильно заштриховать множество решений неравенства на числовой прямой, воспринимаем знак неравенства как стрелку. Стрелка указывает направление штриховки.
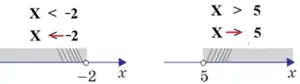
8. Знаки «больше» и «меньше»
Один из случаев, когда нужно запомнить два понятия по определению, то есть без логического обоснования. В советское время советовали мысленно перечеркнуть нижнюю часть знака: если получится 7, то это знак «больше», если 4 - то знак «меньше».
Больше: цифра 7, большое число. Меньше: цифра 4, маленькое число.

9. Запоминание значений математических констант π и е

В разделе «Тригонометрия» большое количество тригонометрических формул, которые ребята плохо запоминают. На помощь придет мнемотехника.
10. Определение тригонометрических функций
Еще один из случаев, когда нужно запомнить два понятия по определению, а значит, возникает возможность их перепутать.
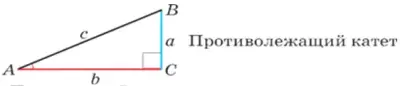
сИнус - прОтиволежащий катет к гипотенузе
кОсинус - прИлежащий катет к гипотенузе.
Применение чередования О и И

11. Решение простейших тригонометрических уравнений sinx = a, cosx=a
Ребята забывают, какую хорду и в каком случае нужно рассматривать. Поможет произнесение слов «синус» и «косинус». Ударная гласная «и» вытягивает рот в направлении «↔», значит на круге при решении уравнения sinx = a надо провести горизонтальную хорду, ударная «о» вытягивает рот в направлении «↕», значит при решении уравнений вида cosx = a будем проводить вертикальную хорду.
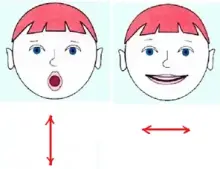
12. Знаки тригонометрических функций
Обучающиеся как правило запоминают, что у тангенса и котангенса знаки располагаются крест-накрест, но путают, знаки синуса и косинуса. Я подсказываю правило: произносим слова «синус» и «косинус» выделяя ударную гласную и фиксируя при этом, в каком направлении вытягивается рот. При произнесении слова «синус» ударная гласная «и» вытягивает рот в направлении «↔», значит, у синуса знаки расположены горизонтально. Аналогично, при произнесении слова «косинус», ударная гласная «о» вытягивает рот в направлении «↕», значит, у косинуса знаки расположены вертикально.
13. Вторая производная и выпуклость функции
Используем «правило смайлика».
Правило: Если вторая производная отрицательная, то функция выпуклая вверх. Если вторая производная положительная, то функция выпуклая вниз.Ассоциация: если «минус», то «смайлик» грустный, если «плюс», то «смайлик» веселый.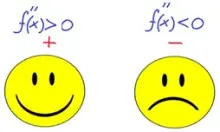
14. Правило запоминания формул сокращенного умножения
![]()
В формулах сокращенного умножения всегда длинная левая часть дополняется короткой правой и наоборот.
Потеря удвоенного произведения в формулах квадрата двучлена самая распространенная ошибка. Дети видят, что если левая и правая части тождества становятся короткими- формула неверна.
15. Решение простейших тригонометрических уравнений sinx = a, cosx=a
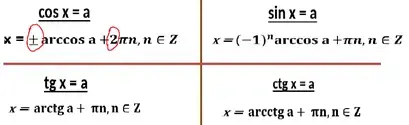
При решении простейших тригонометрических уравнений первые три функции sin x, tg x,ctg x имеют период π, а функция cos x период 2π
Во всех формулах есть πn. Кроме формулы с арккосинусом.
Там стоит 2πn. Ключевое слово - два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там - два. Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет 2πn.
Заключение
Приемы мнемотехники помогают реализовать важнейший дидактический принцип обучения - принцип наглядности.
Я уверена, что приёмы мнемотехники на уроках математики необходимы так как это:
- позволяет сделать обучение простым и доступным для каждого ученика;
- развивает память учащихся, ребята могут с легкостью вспомнить правила и формулы;
- приемы находят живой отклик у ребят и это позволяет повысить интерес к предмету.
Конечно, большая часть мнемотехник, приведенных здесь придуманы не мной. Но найдя и попробовав их один раз я стала использовать их в своей работе, и результат не заставил себя ждать. Дети с лёгкостью вспоминают определения и формулы, даже если прошло достаточно много времени.
Иногда ребята сами могут предложить довольно неожиданный приём запоминания того или иного правила, и это здорово!
Сложные логические рассуждения, непривычная терминология пугают школьников, отворачивают от предмета. Дети теряют интерес к уроку, предмету в целом. Мнемотехника на уроках дает возможность переключения, своеобразного отвлечения от науки на уровень житейских ассоциаций, игры, воображения и фантазии. Для слабых учащихся мнемотехника это шанс запомнить объяснение, правило, алгоритм, формулу.
Конечно, не надо вводить элементы мнемотехники в изучении всех разделов математики. Её применение необходимо на «провальных» моментах и темах, где допускается большое количество типичных ошибок.
Литература
- Беседы по рисункам. Уроки Ушинского. - М.: Сфера, 2014.
- Гончаров Н.К. Педагогическая система К.Д.Ушинского / Н.К.Гончаров. - М.: Педагогика, 2019.
- Козаренко В.А. Учебник мнемотехники. Система запоминания «Джордано» Сайт Mnemonikon (http://www.mnemotexnika.narod.… - М.:, 2007.
- Зиганов М.А., Козаренко В.А. Мнемотехника. Запоминание на основе визуального мышления // М.: Школа рационального чтения, 2001.