Презентация к занятию «Моделирование при решении текстовых задач начального курса математики» для студентов 2-го курса СПО
Скачать презентацию (4.41 МБ)
Сопроводительная форма к презентации для преподавателя
«Моделирование при решении текстовых задач начального курса математики» для студентов 2 курса СПО, обучающихся на базе 9-ти классов по специальности 44.02.02 преподавание в начальных
классах
|
Цель |
Организация деятельности обучающихся по формированию умения применять моделирование при решении текстовых задач начального курса математики в соответствии с его этапами. |
|
Задачи |
|
|
Описание |
Предметным результатом дистанционного занятия «Моделирование при решении текстовых задач начального курса математики» является применение приема моделирования при решении текстовых
задач начального курса математики в соответствии с его этапами.
|
|
Ключевые слова |
моделирование, текстовые задачи начального курса математики, начальная школа, СПО |
Содержание занятия
|
Здравствуйте, уважаемые студенты! Добро пожаловать на видеозанятие! Занятие рассчитано на студентов 2 курса, которые учатся на базе основного общего образования по специальности 44.02.02 Преподавание в начальных классах.
|
||
|
ВКЛ |
Слайд 2 |
(ждём 5 секунд) |
|
ВКЛ |
Слайд 3 |
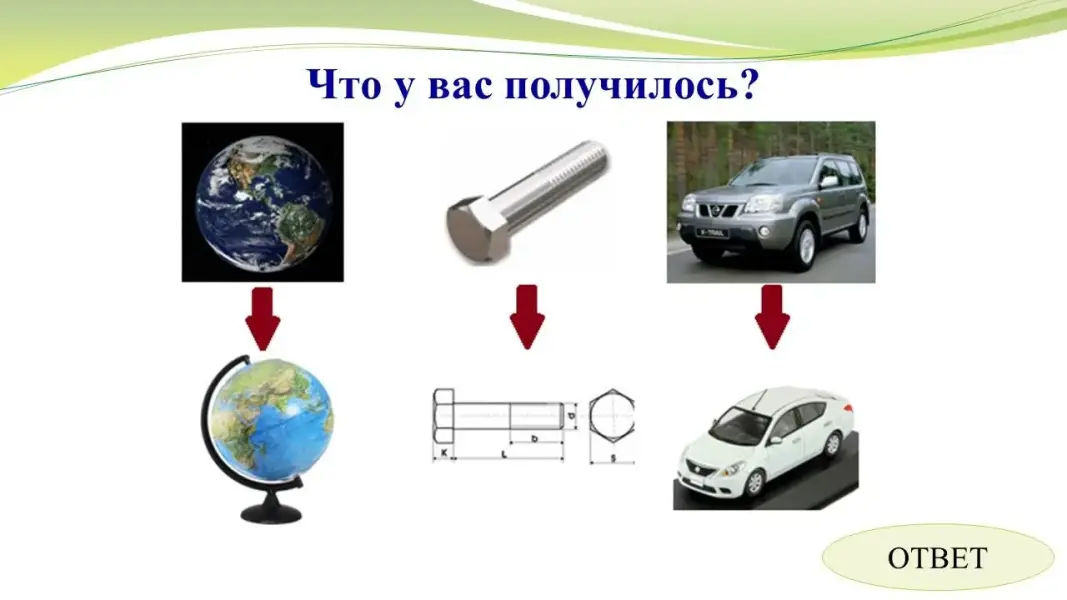
Что у вас получилось? (ждём 2 секунды) |
|
Слайд 3 |
Хорошо! |
|
|
ВКЛ |
Слайд 4 |
Между чем вы устанавливали соответствие? |
|
Слайд 4 |
Между моделируемыми объектами и их моделями.
|
|
|
ВКЛ |
Слайд 5 |
Какая модель будет здесь? (ждём 5 секунд) |
|
Возможно, данная ситуация вызвала у вас затруднение.
|
||
|
ВКЛ |
Слайд 6 |
Как вы думаете, какая тема данного занятия? (ждём 2 секунды) |
|
Слайд 6 |
«Моделирование при решении текстовых задач начального курса математики» |
|
|
ВКЛ |
Слайд 7 |
Какую же поставим цель занятия? |
|
Слайд 7 |
Изучение приема моделирования при решении текстовых задач начального курса математики.
|
|
|
ВКЛ |
Слайд 8 |
Какие задачи вы предлагаете решить для достижения поставленной цели? |
|
Слайд 8 |
Первая задача. Определить понятие «моделирование».
|
|
|
ВКЛ |
Слайд 9 |
Итак, нам предстоит решить ряд задач для достижения поставленной цели. |
|
ВКЛ |
Слайд 10 |
Приступим же к решению первой задачи.
|
|
ВКЛ |
Слайд 11 |
Как бы вы описали понятие «моделирование»? |
|
Слайд 11 |
Моделирование позволяет изучать не интересующий нас объект, а его модель. |
|
|
Слайд 11 |
Модель замещает интересующий нас объект с точки зрения познания. |
|
|
ВКЛ |
Слайд 12 |
Любая ли «модель» будет являться моделью какого-то объекта? |
|
Слайд 12 |
Нет, не любая, только та, которая соответствует объекту-оригиналу относительно его свойств. |
|
|
ВКЛ |
Слайд 13 |
Послушайте, какое определение, дал понятию «моделирование»
|
|
ВКЛ |
Слайд 14 |
Моделирование - это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая
вспомогательная искусственная или естественная система (модель):
|
|
ВКЛ |
Слайд 15 |
Как можно адаптировать определение Ляпунова Алексея Андреевича под ситуацию моделирования текстовых задач? |
|
Слайд 15 |
Моделирование при решении текстовых задач - это исследование условия задачи, при котором:
|
|
|
ВКЛ |
Слайд 16 |
Итак, мы решили 1-ю задачу нашего плана - определили понятие «Моделирование» |
|
ВКЛ |
Слайд 17 |
Перейдём ко второй задаче - Познакомимся с моделями, используемыми при решении текстовых задач начального курса математики |
| Модели бывают разные, и поскольку в литературе нет единообразия в их названиях, уточним терминологию, которую будем использовать в дальнейшем. | ||
|
ВКЛ |
Слайд 18 |
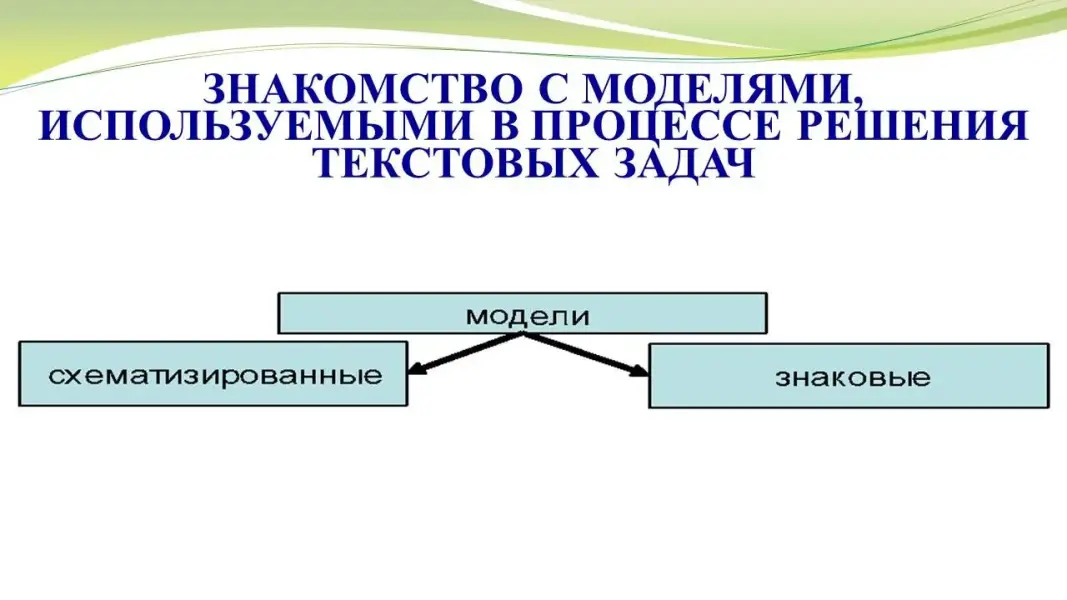
Все модели можно разделить на схематизированные и знаковые по видам средств, используемых для их построения. |
|
ВКЛ |
Слайд 19 |
Схематизированные модели, в свою очередь, делятся на вещественные и графические в зависимости от того, какое действие они обеспечивают |
|
ВКЛ |
Слайд 20 |
Вещественные модели обеспечивают физическое действие с предметами |
|
ВКЛ |
Слайд 21 |
или с их заместителями |
|
ВКЛ |
Слайд 22 |
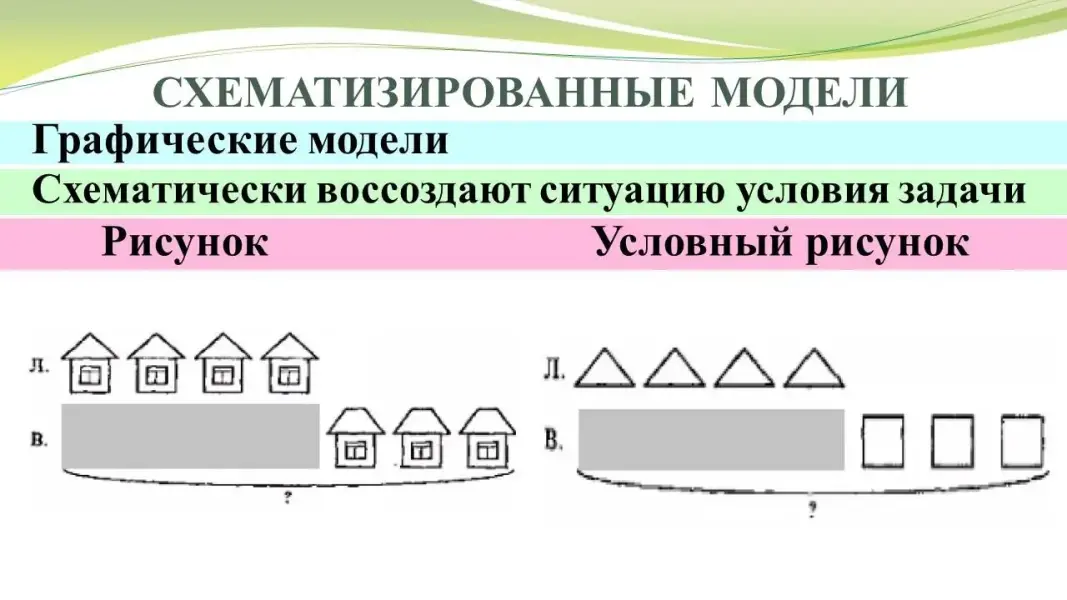
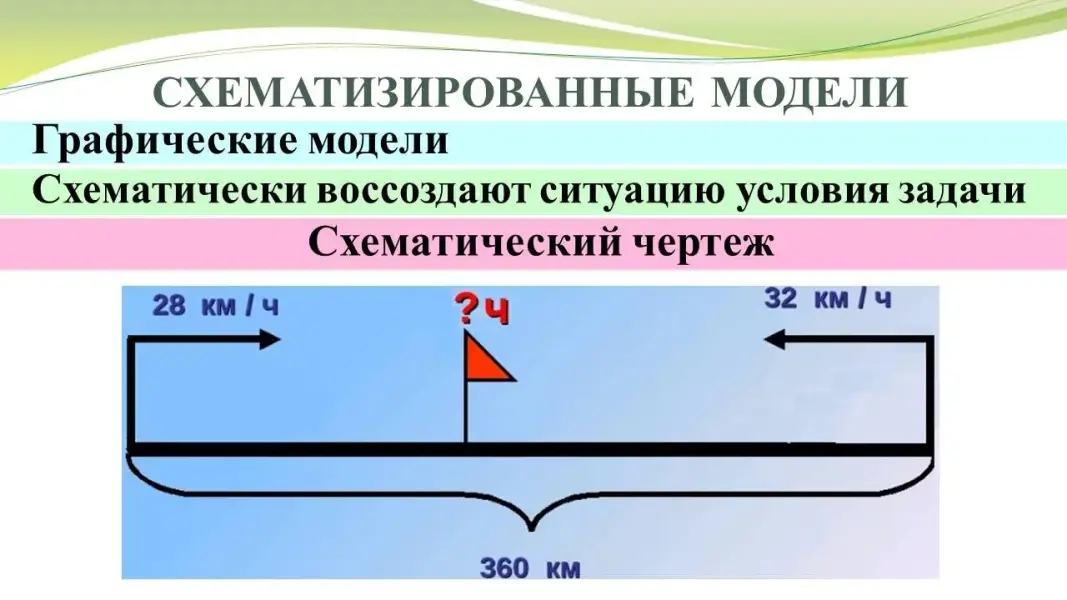
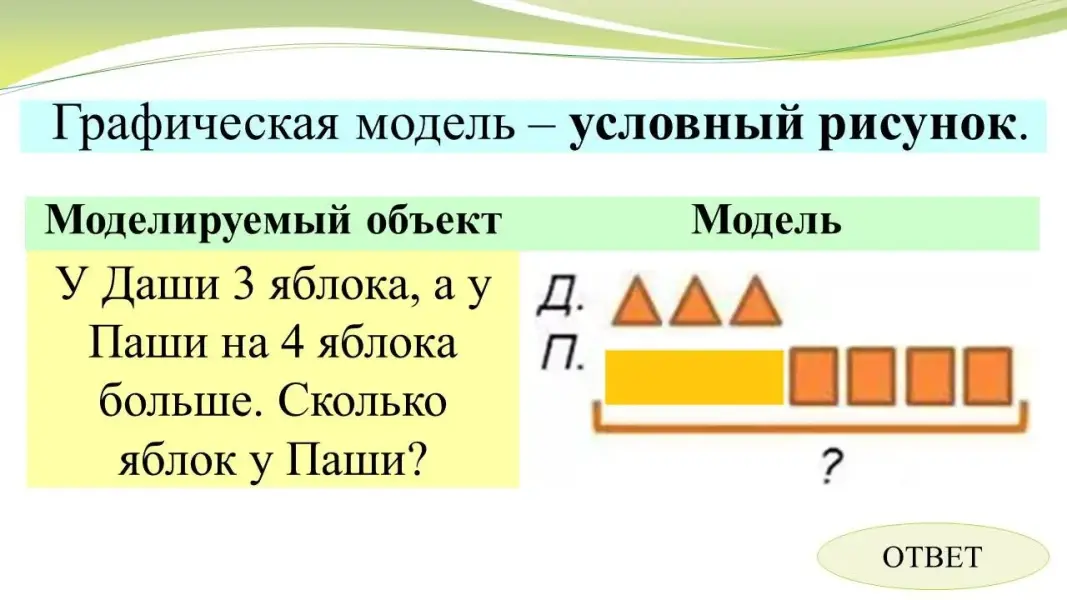
Графические модели схематически воссоздают ситуацию условия задачи в виде рисунка или условного рисунка. |
|
ВКЛ |
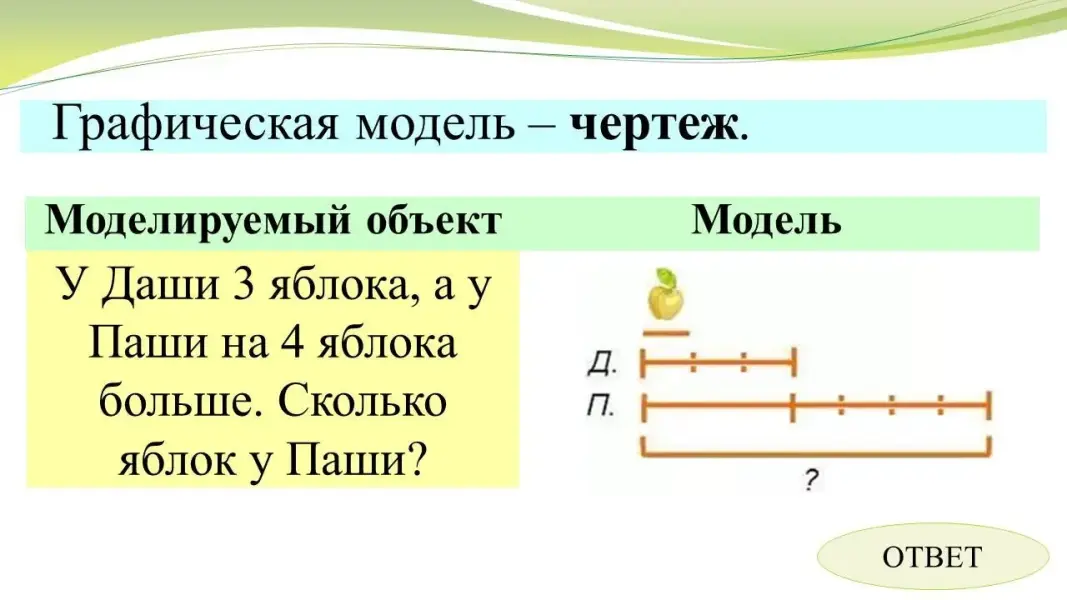
Слайд 23 |
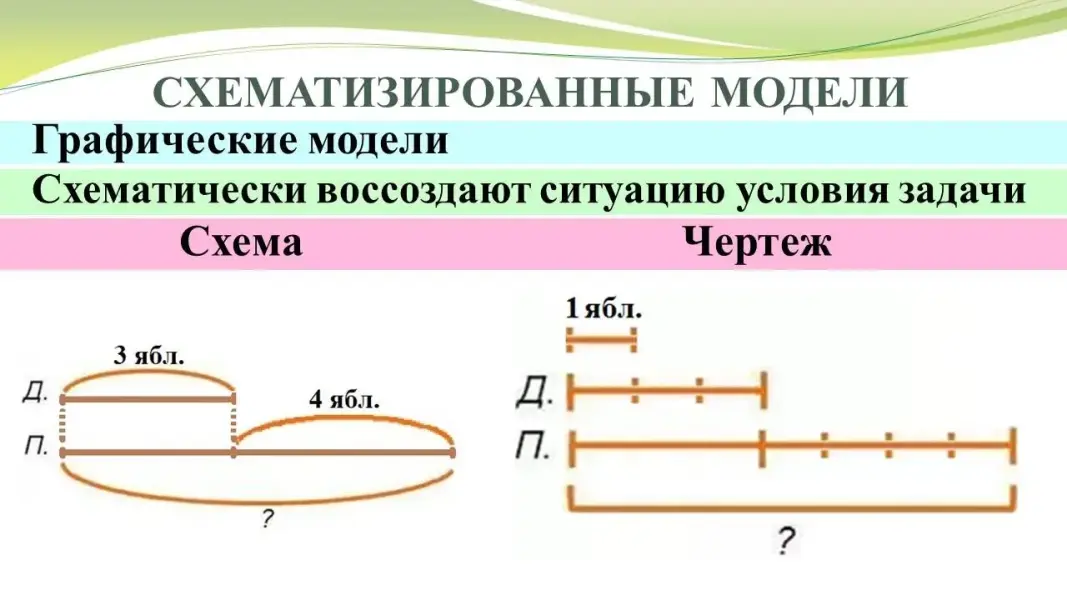
А также в виде, например, схемы, чертежа |
|
Слайд 24 |
или схематического чертежа. |
|
|
ВКЛ |
Слайд 25 |
Знаковые модели делятся на словесные и математические. |
|
ВКЛ |
Слайд 26 |
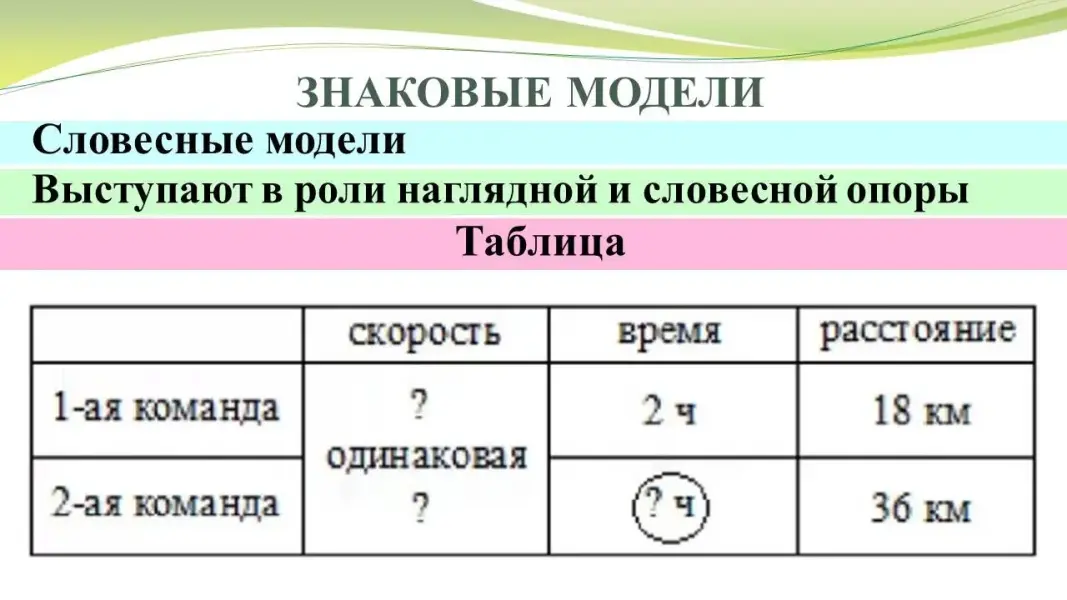
Словесные модели выступают в роли наглядной словесной опоры в виде краткой записи |
|
ВКЛ |
Слайд 27 |
Или в виде таблицы, которая используется, если в задаче имеются несколько взаимосвязанных величин, каждая из которых задана одним или несколькими значениями. |
|
ВКЛ |
Слайд 28 |
Выше перечисленные модели, такие как: вещественные, графические и словесные относятся к вспомогательным видам моделей.
|
|
ВКЛ |
Слайд 29 |
В данной таблице мы видим, что к вспомогательным видам моделей относятся: вещественные, графические и словесные.
|
|
ВКЛ |
Слайд 30 |
Итак, мы решили 2-ю задачу нашего плана. |
|
ВКЛ |
Слайд 31 |
Перейдём к третьей задаче - определим этапы моделирования текстовой задачи |
|
ВКЛ |
Слайд 32 |
Как бы вы разбили процесс моделирования на этапы? |
|
Слайд 32 |
1. После прочтения задачи составили бы краткую запись (модель), соответствующую условию. |
|
|
Слайд 32 |
2. Записали бы решение задачи (либо выражением, либо по действиям с пояснениями). |
|
|
Слайд 32 |
3. Записали бы ответ задачи. |
|
| Точное количество этапов моделирования текстовых задач, не определено, но моделируя решения задач начального курса математики, обычно выделяют три этапа: | ||
|
ВКЛ |
Слайд 33 |
Первый. Перевод условия задачи на математический язык
|
|
ВКЛ |
Слайд 34 |
На первом этапе выделяют необходимые для решения данные и искомые и математическими способами описывают связи между ними. |
|
ВКЛ |
Слайд 35 |
На втором этапе выполняют необходимые арифметические действия либо решают уравнение, если задача решается алгебраическим методом. |
|
ВКЛ |
Слайд 36 |
На заключительном этапе переводят полученное решение на тот язык, на котором была сформулирована исходная задача. |
|
ВКЛ |
Слайд 37 |
Рассмотрим пример моделирования при решении текстовой задачи алгебраическим методом.
|
|
ВКЛ |
Слайд 38 |
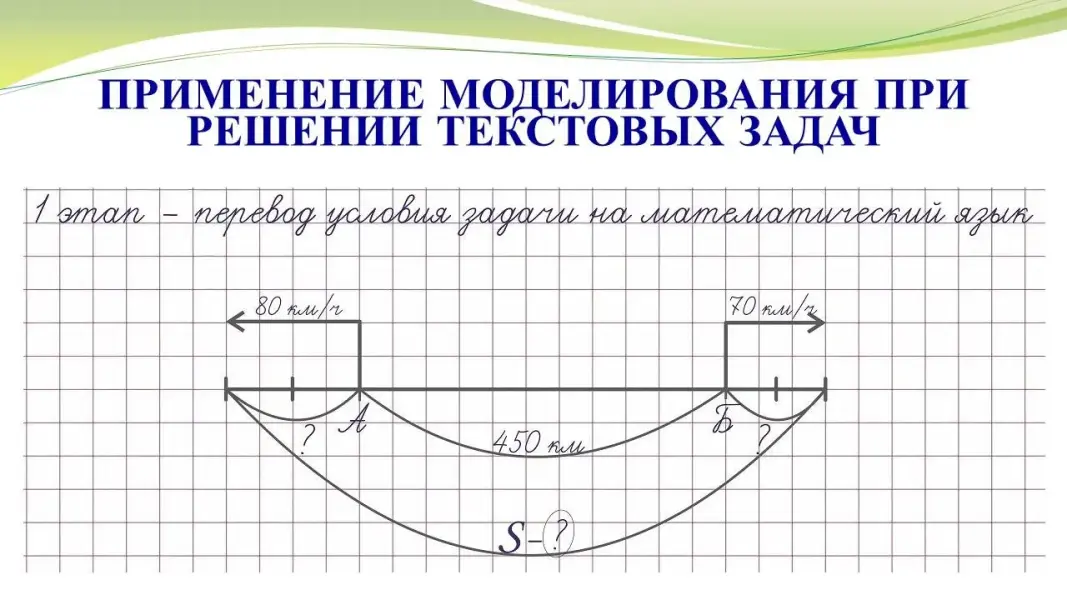
1 этап. Переведём условие задачи на математический язык |
|
Слайд 38 |
Обозначим через x первоначальное число пассажиров во втором вагоне, тогда число пассажиров в первом вагоне будет 2x.
|
|
|
Слайд 38 |
Уравнение - это математическая модель данной задачи. |
|
|
ВКЛ |
Слайд 39 |
2 этап. Выполним внутримодельное решение - решим полученное уравнение. |
|
Слайд 39 |
Переносим в левую часть члены уравнения, содержащие x, а в правую - не содержащие x, причем у переносимых членов знаки меняем на противоположные: 2x - x = 7 + 3.
|
|
|
ВКЛ |
Слайд 40 |
3 этап. Интерпретация |
|
Слайд 40 |
Используем полученное решение, чтобы ответить на вопрос задачи. |
|
|
Слайд 40 |
Запишем ответ: во втором вагоне было первоначально 10 человек, а в первом - 20 человек. |
|
|
ВКЛ |
Слайд 41 |
Прием моделирования заключается в том, что для исследования текстовой задачи строят модель подобную в каком-то отношении условию данной задачи. |
|
Слайд 41 |
Построенный новый объект изучают, с его помощью находят ответы на поставленные вопросы в условии задачи. |
|
|
Слайд 41 |
а затем результат переносят на первоначальный объект, то есть на текстовую задачу. |
|
|
ВКЛ |
Слайд 42 |
Таким образом, мы решили 3-ю задачу нашего плана. |
|
ВКЛ |
Слайд 43 |
Перейдём к заключительной, четвёртой задаче - применим моделирование при решении текстовых задач начального курса математики на «практике». |
|
ВКЛ |
Слайд 44 |
Итак, задание: Применяя моделирование, решите текстовую задачу в соответствии с этапами моделирования. |
|
Два мотоциклиста выехали одновременно из двух пунктов, расстояние между которыми 450 км. Скорость одного из них 80 км/ч, скорость другого 70 км/ч. На каком расстоянии будут они друг от друга через 2 часа, если они движутся в противоположных направлениях. |
||
|
Слайд 44 |
Остановите видеозанятие для самостоятельного выполнения задания, а затем запустите его снова, чтобы проверить себя. |
|
|
Итак, перейдем к самопроверке |
||
|
ВКЛ |
Слайд 45 |
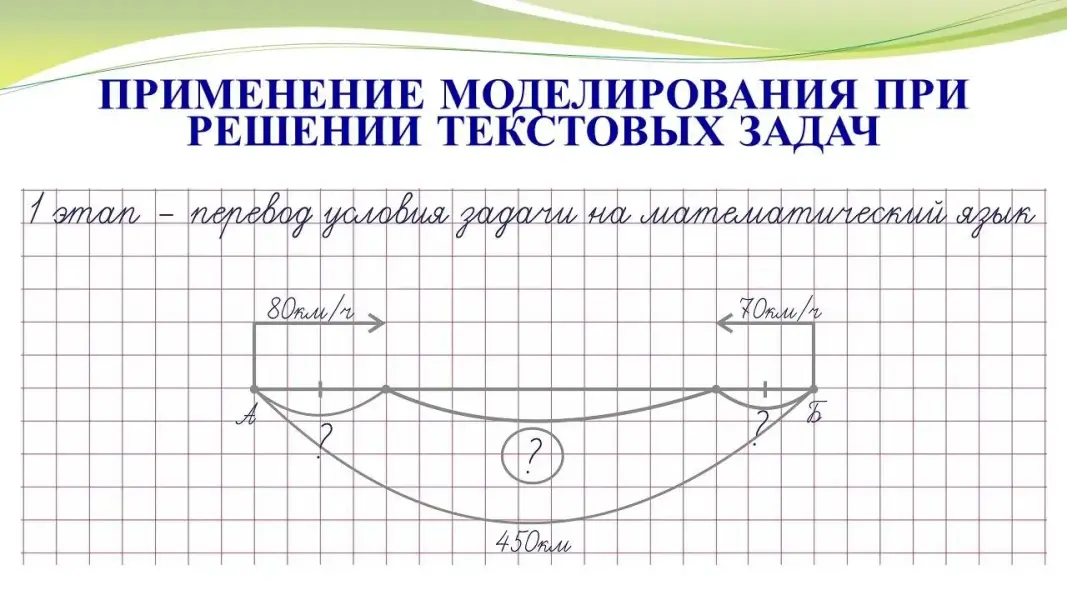
Сверьте 1-й этап моделирования - перевод условия задачи на математический язык. |
|
Обратите внимание!
|
||
|
ВКЛ |
Слайд 46 |
Посмотрите на памятку ещё раз (ждём 2 секунды) |
|
ВКЛ |
Слайд 47 |
Сверьте 2-й этап моделирования - внутримодельное решение.
|
|
ВКЛ |
Слайд 48 |
Сверьте 3-й этап моделирования - интерпретация.
|
|
ВКЛ |
Слайд 49 |
Попробуйте ещё!
|
|
Два мотоциклиста выехали одновременно из двух пунктов, расстояние между которыми 450 км. Скорость одного из них 80 км/ч, скорость другого 70 км/ч. На каком расстоянии будут они друг от друга через 2 часа, если они движутся навстречу друг другу. |
||
|
Слайд 49 |
Остановите видеозанятие для самостоятельного выполнения задания, а затем запустите его снова, чтобы проверить себя. |
|
|
Перейдем к самопроверке |
||
|
ВКЛ |
Слайд 50 |
Сверьте 1-й этап моделирования - перевод условия задачи на математический язык. |
|
Слайд 50 |
Обратите внимание!
|
|
|
ВКЛ |
Слайд 51 |
Посмотрите на памятку ещё раз (ждём 2 секунды) |
|
ВКЛ |
Слайд 52 |
Сверьте 2-й этап - внутримодельное решение (ждем 5 секунд) |
|
ВКЛ |
Слайд 53 |
Сверьте 3-й этап - Интерпретация
|
|
ВКЛ |
Слайд 54 |
Итак, мы решили все задачи для достижения поставленной цели - изучение приема моделирования при решении текстовых задач начального курса математики.
|
|
ВКЛ |
Слайд 55 |
Какая модель будет здесь? (ждём 5 секунд) |
|
ВКЛ |
Слайд 56 |
Здесь могут быть разные варианты видов моделей. |
|
ВКЛ |
Слайд 56 |
Например, графическая модель в виде рисунка.
|
|
ВКЛ |
Слайд 57 |
Позднее, можно переходить на выполнение моделирования в виде условного рисунка |
|
ВКЛ |
Слайд 58 |
Если числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины, применяют моделирование в виде чертежа. |
|
ВКЛ |
Слайд 59 |
Для записи условия задачи с помощью опорных слов, применяют словесную модель в виде краткой записи. |
|
ВКЛ |
Слайд 60 |
Любая из этих моделей призвана дать обучающимся возможность более полно увидеть отражение зависимостей между данными и искомыми в задаче, увидеть задачу в целом. |
| В заключение занятия необходимо отметить следующее: если учитель начальных классов в своей профессиональной деятельности активно применяет моделирование при решении текстовых задач, это позволяет ему не только найти оптимальные варианты решения и количественную характеристику какого-либо компонента заявленной текстовой задачи, но и формировать метапредметные умения у младших школьников, позволяющие решать учебные и практические задачи. | ||
|
ВКЛ |
Слайд 61 |
Основной источник, используемый при подготовке занятия, вы видите на данном слайде. |
|
Занятие окончено! До свидания! |
||