Геометрический подход при доказательстве неравенств
Введение
Неравенства играют значительную роль в различных областях математики, так как они дают возможность отыскивать решения задач на нахождение областей, в которых одна величина больше или меньше другой величины.
Задачи на доказательство неравенств одни из самых трудных и интересных из традиционного цикла обучающих задач в школе. Применяемые для доказательства неравенств идеи почти столь же разнообразны, как и сами неравенства.
При доказательстве неравенств можно использовать как аналитический, так и геометрический подход к доказательству неравенства. При аналитическом подходе к доказательству неравенств достаточно отыскать знак разности левой и правой частей неравенства и, в зависимости от полученного результата, сделать вывод. В конкретных ситуациях общие методы решения часто приводят к трудоемким решениям рассматриваемых задач.
Геометрическая интерпретация множества решений неравенства, а также использование понятий пересечения и объединения множеств, помогают при решении неравенств и задач, которые при аналитическом подходе привели бы к сложным, длинным и труднообозримым вычислениям.
В работе на нескольких примерах продемонстрирован геометрический подход к решению и доказательству неравенств.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Сначала опишем схему главных действий при решении или доказательстве неравенств. Эту схему можно представить следующим образом:
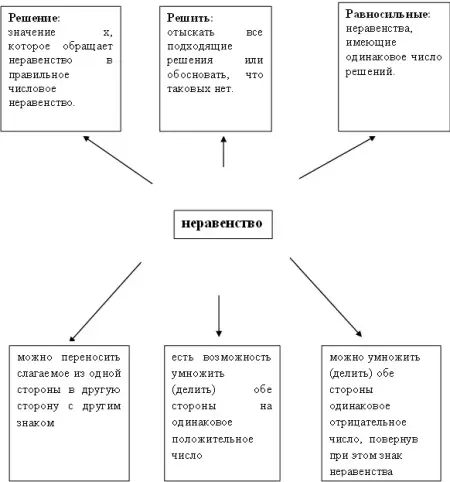
В таблице 1 представленные основные типы изучаемых неравенств.
Таблица 1 - Виды неравенств

1.1. Методы решения неравенств
Существуют различные подходы к решению неравенств.
- Метод интервалов (Таблица 2),
- Введения новой переменной,
- Функционально-графический,
- Равносильных преобразований,
- Метод возведения обеих частей неравенства в одну и ту же степень,
- Метод умножения двух частей неравенства на один множитель,
- Метод оценки,
- Метод рационализации, т.е. сведение к рациональным неравенствам.
Перечислим типы промежутков, которые используются при подстановке задачи или выписывания ответа решенной задачи.
Таблица 2 - Числовые промежутки
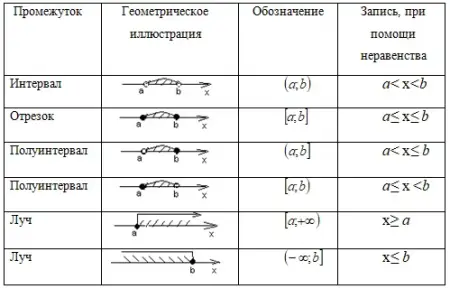
Квадратные неравенства [1, 105] - это неравенства указанные в таблице 1, которые имеют вид ax2+bx+c>0, ax2+bx+c<0, ax2+bx+c≤0, ax2+bx+c≥0, где а ≠ 0.
В случае, когда квадратное уравнение ax2+bx+c=0 обладает двумя вещественными корнями, для нахождения решения квадратного неравенства , разложив левую часть квадратного неравенства на два линейных множителя, сводится к решению системы двух линейных неравенств.
Доказать квадратное неравенство можно графическим методом (Таблица 3). Квадратичная функция обычно задается формулой у =ax2+bx+c, где a ≠ 0. Тогда решение квадратного неравенства сводится к отысканию нулей квадратичной функции и промежутков, на которых квадратичная функция принимает положительные или отрицательные значения.
Таблица 3 - Графическое изображение
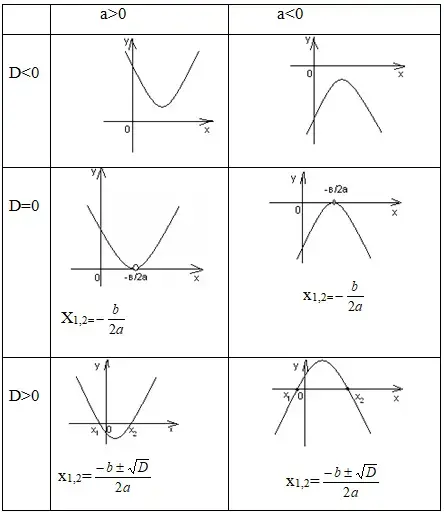
Итак, использование координатной плоскости и графиков квадратичной функций позволяет применить геометрические методы к решению и исследованию неравенств с одним и с двумя неизвестными. Геометрические приемы эффективно применяются для изображения результатов исследования там, где чисто аналитическая запись громоздка. Характерным примером служат графические схемы, к которым приводят различные случаи, возникающие при решении неравенства ax2+bx+c>0. В результате систематического использования графических приемов, учащиеся привыкают пользоваться такими схемами.
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
(примеры использования геометрического подхода при решение и доказательстве неравенств)
Основная ценность графического подхода к решению неравенств состоит в том, что уже схематическое изображение графиков функций часто показывает, что неравенство выполняется в интервалах, ограниченных такими характерными точками, как точки пересечения графиков между собой или точки пересечения графика у = f(х) с осью Ох или Оy. Отыскание этих точек является уже несколько более легкой задачей: оно сводится к решению уравнений.
Пример 1. [7, 176] Найдите наименьшее значение функции
Решение. Решение данной задачи с помощью производной приведет к достаточно большим вычислениям. Попробуем сформулировать условие задачи по-другому.
![]()
Выделим полные квадраты в подкоренных выражениях:
Теперь легко видеть, что первый корень есть расстояние от точки на оси абсцисс до одной из точек с фиксированными В(1, -2) или (1, 2) координатами, которые не зависят от , а второй корень
расстояние от той же точки оси абсцисс до одной из точек С(8, 5) или (8, -5). Итак, значение функции y(x) представляет собой сумму расстояний ВА + АС = А + АС = А + А (в силу симметричности точек В и
и С и относительно оси Ох). Значит, чтобы найти наименьшее значение функции, достаточно найти такую точку на оси абсцисс, сумма расстояний от которой до данных точек будет минимальна. Так как точки B
и C расположены по разные стороны от оси абсцисс Ох, то можно утверждать, что точка А, которую ищем, будет точкой пересечения прямой ВС с осью ОХ, в противоположном случае сумма расстояний будет
больше, что следует из неравенства треугольника. Аналогично рассуждаем при рассмотрении точек и . Напишем уравнение прямой ВС, как уравнение прямой по двум точкам, а затем найдем ее пересечение с
осью абсцисс, пологая y=0. Легко проверить, что прямая с заданным уравнением проходит через точки В и С. Найдем абсциссу точки пересечения прямой с Ох Пологая у=0. Получим ![]() . Тогда наименьшее расстояние равняется.
. Тогда наименьшее расстояние равняется.
![]()
Аналогичные рассуждения проводятся для второго случая. Ответ будет тот же самый.
Ответ: ![]()
Пример 2. Докажите, что при 1 < x < 2 верно неравенство
![]()
Решение. Строим графики функций y = x; y = ![]() . Первый из них нам известен, второй представляет собой часть
параболы, лежащую в верхней полуплоскости. Из чертежа (Рисунок 1) видно, что неравенство удовлетворяется в интервале (a; 2) левый конец которого - корень уравнения
. Первый из них нам известен, второй представляет собой часть
параболы, лежащую в верхней полуплоскости. Из чертежа (Рисунок 1) видно, что неравенство удовлетворяется в интервале (a; 2) левый конец которого - корень уравнения ![]() = x.
= x.
Решаем это уравнение.
По определению арифметического квадратного корня
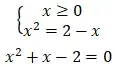
x1 = -2 (не удовлетворяет условию); x2 = 1. Значит а = 1.
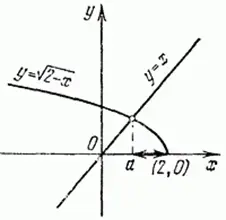
Рисунок 1 - Графическое изображение решения неравенства
Пример 3. Докажите, что при ![]() верно неравенство
верно неравенство ![]()
Решение. Строим график функции на (Рисунке 2) пунктиром показан график функции ![]() после чего график y =
log3x показан сплошной линией. Далее проведена прямая y = 1. Сразу видно, что данному неравенству будут удовлетворять значения х из двух симметричных интервалов:
(-b; -a), (a; b) Здесь через
после чего график y =
log3x показан сплошной линией. Далее проведена прямая y = 1. Сразу видно, что данному неравенству будут удовлетворять значения х из двух симметричных интервалов:
(-b; -a), (a; b) Здесь через ![]() a,
a, ![]() b обозначены абсциссы точек пересечения прямой
y = 1 с графиком функции, т.е. решения уравнения
b обозначены абсциссы точек пересечения прямой
y = 1 с графиком функции, т.е. решения уравнения
![]()
В силу симметрии достаточно найти решения уравнения при x>0. Поэтому уравнение сводится к
![]()
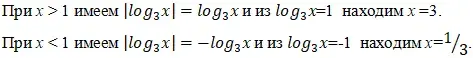
Ясно, что ![]() и множеством решений данного неравенства служит пара симметричных интервалов
и множеством решений данного неравенства служит пара симметричных интервалов
![]()
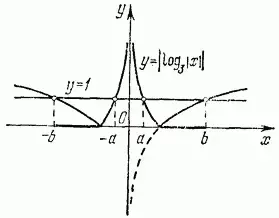
Рисунок 2 - Изображение решения неравенства
Таким образом, неравенства - это часто встречающийся вспомогательный инструмент. В каждой области математики можно указать основные результаты, которые формулируются в виде неравенств. В некоторых разделах математики, неравенства встречаются чаще, чем равенства. Можно сказать, что решение каких-либо важных с практической точки зрения неравенств, находятся в виде числа или множества чисел, либо в виде формулы.
Главной сложностью при использовании геометрического подхода считается неочевидность шагов решения. Неравенства, которые были рассмотрены в работе, имеют стандартное аналитическое решения, но эти решения достаточно трудоемкие. Хотя догадаться использовать геометрические соображения нелегко, поэтому целесообразность геометрического подхода - вопрос неоднозначный.
Ситуации, когда применяются свойства функций при нахождении решений неравенств, многочисленны. Применение свойств функций, которые входят в неравенства, дает возможность применять графический-геометрический подход к решению или доказательству неравенств. Умение пользоваться нужными свойствами функций при решений неравенств, позволяют выбирать более эффективный способ решения.
Список использованной литературы
- Байокки К., Вариационные неравенства. Приложения к задачам с свободной границей / К.Байокки, А.Капело. - Москва: СИНТЕГ, 2018. - 278 c.
- Вавилов В.В., Задачи по математике. Уравнения и неравенства / В.В.Вавилов. - М.: Книга по Требованию, 2018. - 237 c.
- Вавилов В.В., Задачи по математике. Уравнения и неравенства. Справочное пособие / В.В.Вавилов, И.И.Мельников, С.Н.Олехник, и др. - М.: Машиностроение, 2007. - 240 c.
- Власова А.П., Логарифмические и показательные уравнения, неравенства, системы уравнений. 10-11 классы / А.П.Власова, Н.И.Латанова. - М.: Дрофа, 2017. - 490 c.
- Гейдман Б.П., Логарифмические и показательные уравнения и неравенства / Б.П.Гейдман. - М.: МЦНМО, 2016. - 185 c.
- Полиа, Г. Изопериметрические неравенства в математике/ Г.Полиа, Г.Сеге. - М.: КомКнига, 2016. - 338 c.
- Шестаков С.А., ЕГЭ 2017. Математика. Задачи с параметром. Задача 18 (профильный уровень)/ Под ред. Ященко. - М.: МЦНМО, 2017. - 288 c.