Урок-игра: “Соревнование по тяжелой атлетике”
Цели урока:
Образовательные:
- повторение, обобщение и систематизация теоретических знаний методов решения тригонометрических уравнений;
- отработка способов решения тригонометрических уравнений;
- развитие графической культуры;
- расширение представления учащихся о решении тригонометрических уравнений в нестандартных ситуациях.
Развивающие:
- развитие мышления, математической речи, внимания, памяти.
Воспитательные:
- воспитание чувства ответственности, культуры общения, общей культуры.
Оборудование: проектор, презентация, карточки.
“Предмет математики настолько серьезен, что полезно
не упускать случая делать его немного занимательным”.
Паскаль
Ход урок
I. Организационный этап. Постановка цели и задач.
Сегодня мы проводим необычный урок. Урок-соревнование командное по тяжелой атлетике по теме “Решение тригонометрических уравнений и неравенств”.
Цель соревнования: повторить, обобщить и систематизировать материал темы; повторить чтение графиков, расширить представление о решении тригонометрических уравнений в нестандартных ситуациях.
В наших соревнованиях принимают участие четыре команды. В каждой команде есть капитан.
Итак, капитаны представьте свои команды: sinx, cosx, tgx, ctgx.
За правильностью хода наших соревнований будет наблюдать жюри.
Наши соревнования будут проходить в несколько этапов. На каждом этапе на помост будут вызываться атлеты определенной категории:
- легкий вес;
- средний вес;
- тяжелый вес;
- супертяжелый вес.
Каждый этап будет оцениваться определенным количеством баллов, которые затем будут переводиться в кг умножением на 10. В результате победителем будет та команда, которая возьмет самый тяжелый вес. Все результаты будут заноситься в таблицу.
II. Актуализация опорных знаний. “Разминка”.
Итак, начинаем I этап подготовительный.
“Разминка”. На этом этапе принимает участие вся
команда. Все должны разогреть свои мышцы,
привести в порядок свои мысли. “Разминка” будет
проходить по кругу (sinx —> cosx![]() tgx
tgx ![]() ctgx).
И состоит она из трех групп заданий.
ctgx).
И состоит она из трех групп заданий.
1 группа.
Проговорить формулу нахождения корней следующих уравнений:
sinx=а, cosx=a, tgx=a, ctgx=a.
2 группа.
Вычислить:
arccos arcsin arctg arccos arcsin )
arctg (- )
arccos 
arcsin arctg arccos 2 arcsin arctg )
3 группа.
Решите уравнения.
sinx= 0 sinx=1 sinx= -1 cosx=0 cosx=1 cosx= -1 tgx=0 tgx=1 tgx= -1 ctgx=0 ctgx=1 ctgx= -1
Жюри сразу же подводит итог “Разминки” и результат заносится в таблицу.
Итак, команды разогрелись. Мы повторили ключевые моменты для решения тригонометрических уравнений и неравенств. Теперь смело можем переходить на следующий этап, “Кто смелее?”.
III. Основной этап.
Конкурс “Кто смелее?”
На помост вызываются тяжелоатлеты легкого веса. Вам будут предложены, три набора карточек: “зеленые”, “желтые”, “красные”. На каждой карточке записано по одному уравнению разного уровня сложности. Каждой команде предоставляется право выбора, из какой группы взять карточку. По одному представителю выходят к доске, тянут карточку, выбранного цвета и решают. Соответственно, если вы решите уравнение по зеленой карточке, то возьмете вес 40 кг (4б*10), по желтой 60 кг, красной – 80 кг.
Каждая команда имеет право на вторую и 3-ю попытку взятия веса (т.е. по две подсказке) если, конечно это будет необходимо.
| I уровень (4б) | II уровень( 6б) | III уровень (8б) |
| зеленые | желтые | красные |
| 2cos |
sin( |
2sinx –sin2x=cos2x |
| 3tg2x= |
cos( |
cosx+cos2x= |
| 2sin |
sin( |
(cosx - 1)2=cos2x - 1 |
| cos( |
cos2x+cosx=-sin2x |
Команды следят за ходом решения. Кто первый готов, тот и отчитывается первый. Жюри сразу же подводит итог.
Итак, мы повторили решение простейших тригонометрических уравнений, можем смело переходить на следующий этап соревнований. “Кто сообразительнее?”
Конкурс. “Кто сообразительнее”.
Правильному применению методов можно научиться только применяя их на разнообразных примерах. Г.Цейтен
Соревнуются тяжелоатлеты среднего веса.
Как часто первое наше затруднение при решении тригонометрических уравнений заключается в том, что мы не видим приема решения таких уравнений.
Назовите типы тригонометрических уравнений.
- Простейшие тригонометрические уравнения.
- Тригонометрические уравнения, сводящиеся к квадратным уравнениям.
- Однородные тригонометрические уравнения первой и второй степени.
- Тригонометрические нестандартные уравнения.
Назовите основные методы решения тригонометрических уравнений:
- Метод разложения на множители.
- Метод введения новой переменной.
- Решение тригонометрических уравнений как однородное.
Перед вами записано 10 уравнений:
| 1 | 2sin2x +5cosx=4 |
| 2 | sinx+sin5x=0 |
| 3 | 2sin(x/4)cos3x – cos3x=0 |
| 4 | 6sinx |
| 5 | |
| 6 | |
| 7 | 2cos2x - cosx – 1=0 |
| 8 | cos2x +9sinx + 4 =0 |
| 9 | sin2x + 9cos2x =5sin2x |
| 10 | 3sin22x + 0,5sin4x=4cos22x |
Тяжелоатлеты среднего веса берут листок с таблицей ответов, следующего типа:
| Уравнения, сводящиеся к квадратным | Уравнения, решаемые разложением на множители | Однородные уравнения первой и второй степени |
Ваша задача: глядя на уравнение, не решая его, определить метод решения, и номер этого тригонометрического уравнения, написать в соответствующий столбец заготовленной таблицы. Как только команды будут готовы, оригинал они сдают, а копию оставляют себе. А затем также по кругу идет проверка (отвечают тяжелоатлеты среднего веса). За каждое верно поставленное уравнение 30 кг (3б*10).
Жюри подводит итог.
Итак, мы повторили основные методы решения тригонометрических уравнений и теперь можем смело приступать к самому тяжелому решению таких уравнений. Т.е. мы переходим на следующий этап соревнований. “Кто больше?”
Конкурс. “Кто больше?”
Каждая команда получает карточку с заданием. Около каждого задания проставлены баллы (*10) в соответствии с уровнем сложности. Атлет тяжелого веса распределяет задания между членами команды (можно с помощью капитана) и каждый приступает к решению на отдельном листочке (подписанном: фамилия и название команды). На все решение дается 7 мин. Как только время истечет, все листочки сдаются. Жюри подводит итог. Какая команда больше решит и правильно, та и возьмет больший вес на данном этапе.
| 1 | 10 б | |
| 2 | 3 - 3cosx=2sin2x | 10 б |
| 3 | 7sin2x +4sin2x=7cos2x | 10 б |
| 4 | 15 б | |
| 5 | 2sin3x |
15 б |
| 6 | tg2x |
10 б |
| 7 | cos2x + 2cos4x=1 | 15 б |
| 8 | cos( |
20 б |
| 9 |  |
20 б |
| 10 | 4sin22x + 3 =4cos2x | 20 б |
По истечении времени команды сдают листы и жюри подводит итог.
Итак, вы применили все свои знания о методах решения тригонометрических уравнений непосредственно в ходе решения.
Но кроме вышеперечисленных приемов решения есть еще один - графический.
Переходим к следующему этапу “Кто быстрее?”.
Конкурс. “Кто быстрее”.
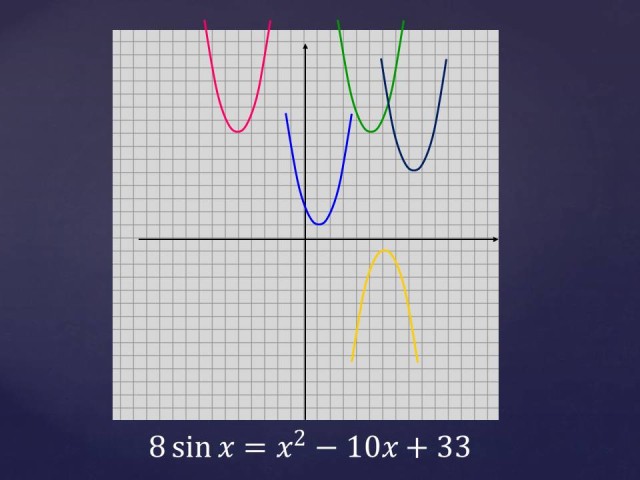
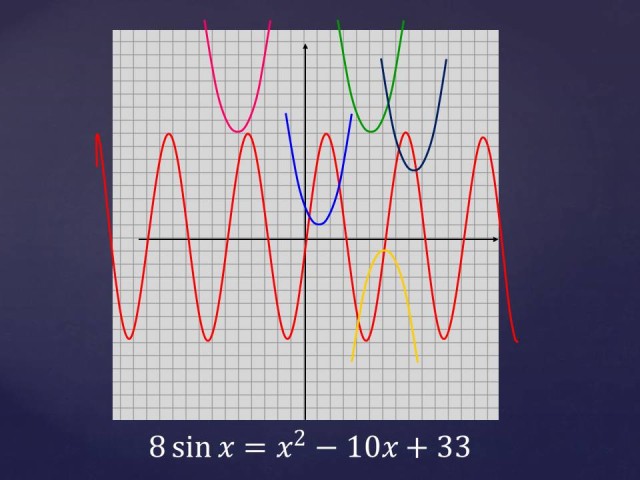
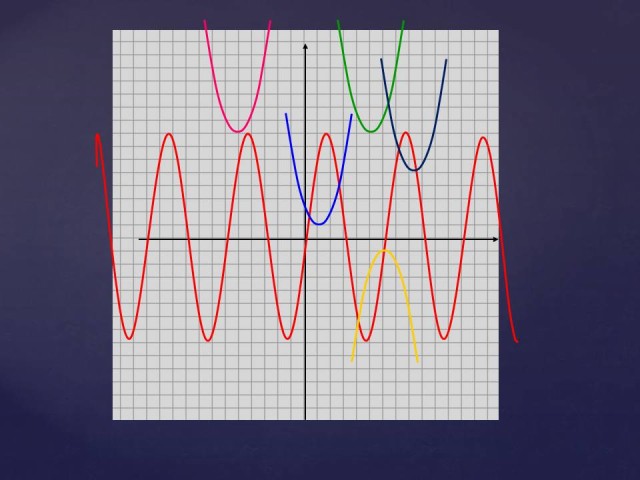
На помост вызываются тяжелоатлеты супер тяжелого веса. Вам предложено решить одно уравнение:
Поможет в решении данного уравнения вам следующая таблица графиков:
Оформляете решение на листочках (т.е. строите графики). Кто первый решит, поднимает руку и т.д. Кто решит быстрее всех и правильно, тот возьмет вес 100 кг (10б * 10), второй – 80 кг; третий – 50 кг; четвертый 30 кг.


По окончании жюри подводят итог.
Итак, мы закончили соревнование атлетов. Вы видите как они прекрасно выступили. Но чтобы достичь таких высоких результатов спортсмены долгое время проводят на тренировках. Вот сейчас и послушаем отчет тренировок. Переходим к следующему этапу “Тренировка” (дом. задание).
Конкурс. “Тренировка”.
Капитаны каждой команды представляет решение физической задачи с применением решения тригонометрических уравнений. Наибольший вес, который может взять капитан равен 100 кг.
Капитаны по очереди представляют задачи.
Пример: Амплитуда колебаний 10 см, а частота 0,5Гц. Написать уравнение х=х(t) и построить его график. Найти фазу и смещение через 1,5 с. Определите, через сколько времени смещение будет 7,1 см?
По окончании жюри подводят итог.
IV. Рефлексия.
| Моё настроение | Своей работой на уроке я | Материал урока мне был | |||||
 |
 |
не доволен | доволен | бесполезен | полезен | скучен | интересен |
V. Домашняя работа. 18.23 (б), 18.33 (б), 18.3 (б).