Приложение определенного интеграла

Тип урока: Комбинированный

Цели урока:

Обучающие:

• систематизация и углубление знаний по теме “определенный интеграл”;
• совершенствование обобщенных умений, связанных с вычислением площадей плоских фигур;
• формирование графической культуры

Развивающие:

• развитие логического мышления;
• развитие самостоятельности и творческой активности;
• развитие общеучебных умений и навыков;

Воспитательные:

• формирование интереса к предмету;
• воспитание культуры общения, интереса к саморазвитию и самопознанию.

Методы активизации учебной деятельности студентов:

• Создание условий приобретения практических навыков;
• Частично-поисковая и исследовательская работа;
• Сообщения студентов;
• Релаксация.

Межпредметные связи:

• Математика, физика, психология, история, философия.

Ход урока

1. Организационный этап. Постановка целей.
2. Проверка домашнего задания.
3. Повторение изученного.
4. Объяснение нового материала.
5. Закрепление новых знаний
6. Релаксация – работа по снятию напряжения и переключение внимания (сообщения студентов)
7. Проверка усвоения нового материала студентами.
8. Подведение итогов (рефлексия, самоанализ).

Организационный момент.

Постановка целей. Взаимное приветствие. Проверка готовности к уроку.

Объяснение нового материала

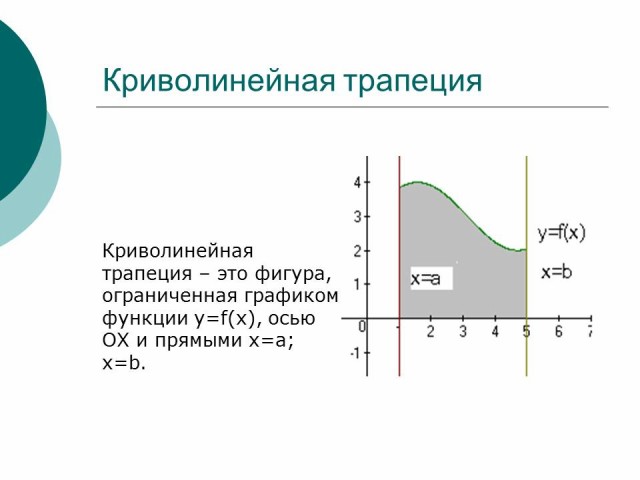
Рассмотрим несколько случаев расположения плоских фигур в декартовой системе координат:

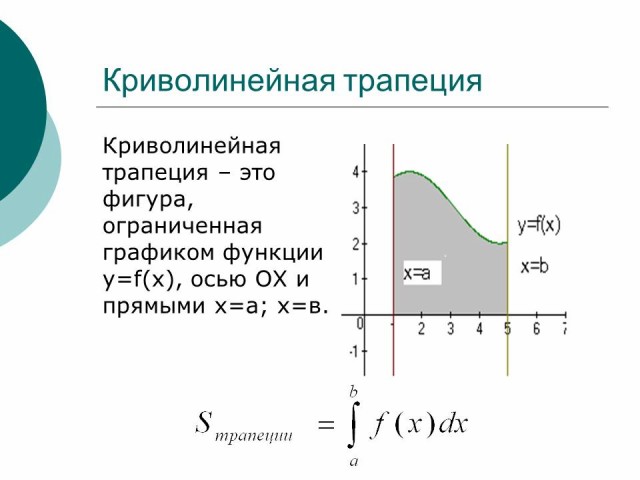
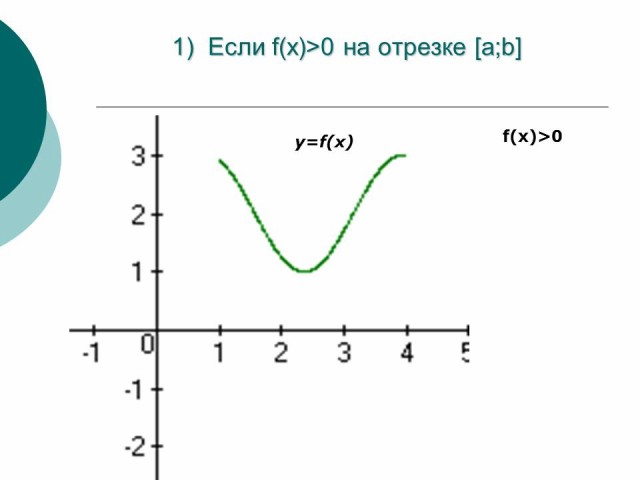
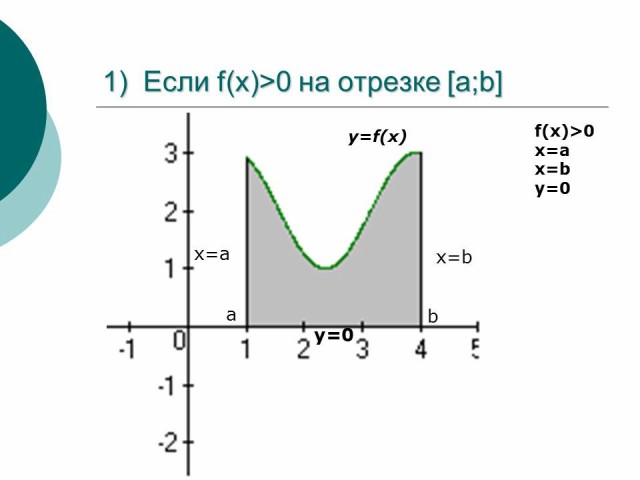
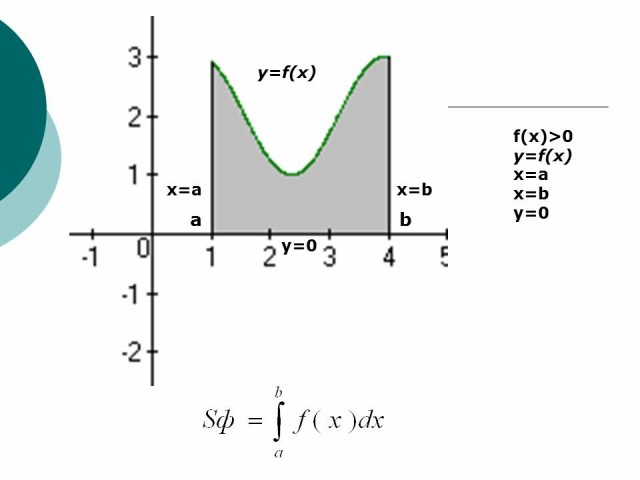
Если функция f(x) > 0 на отрезке [a; b] (т.е. кривая y=f(x) расположена над осью OX), тогда площадь криволинейной трапеции будет равна:

Рисунок 1

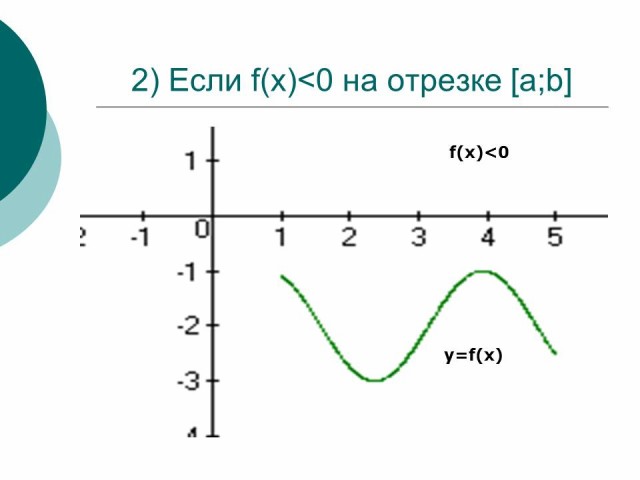
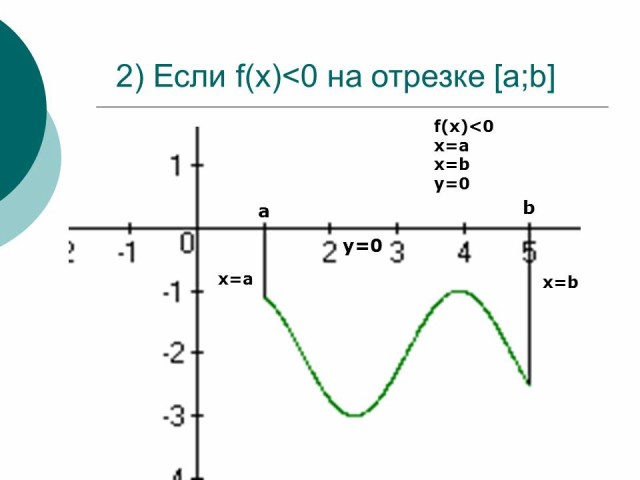
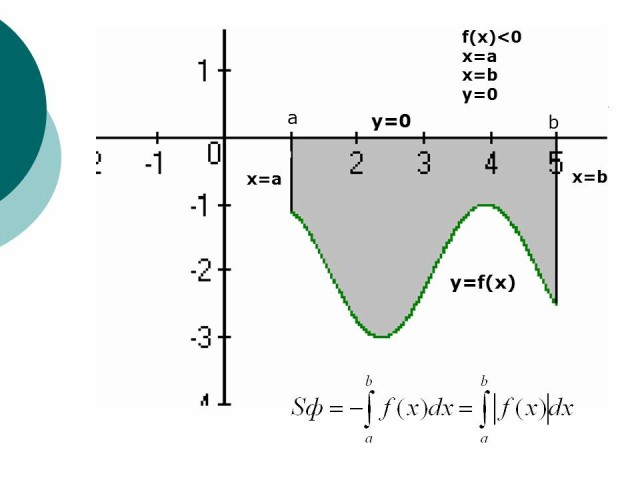
Если функция f(x) < 0 на отрезке [a;b] т.е. кривая y=f(x) расположена под осью OX, то площадь криволинейной трапеции находится по формуле:

Рисунок 2

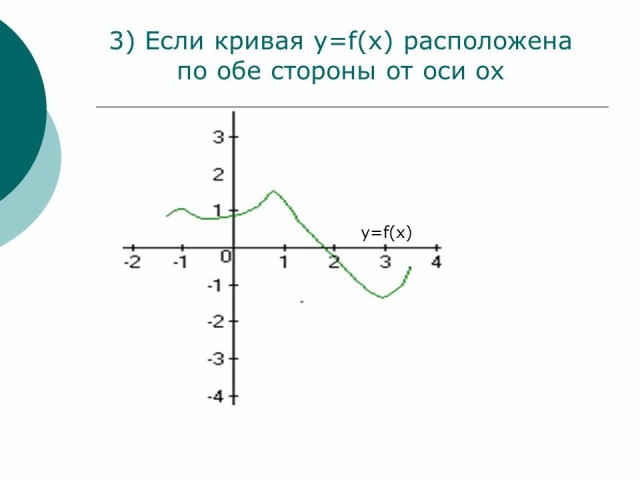
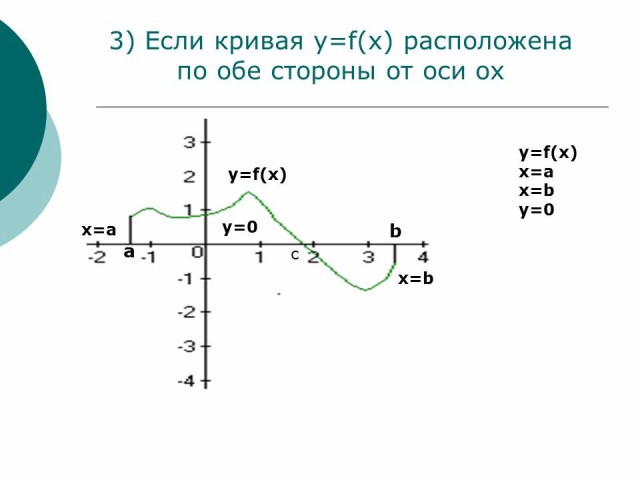
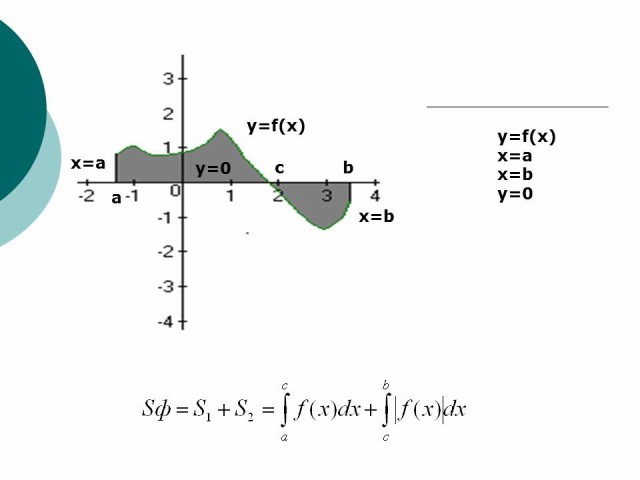
Если фигура, ограниченная кривой y=f(x) осью OX и прямыми x=a , x=b расположена по обе стороны от оси OX, т.е. часть криволинейной трапеции расположена осью OX, а другая часть под осью OX, тогда площадь заштрихованной фигуры равна сумме двух площадей:

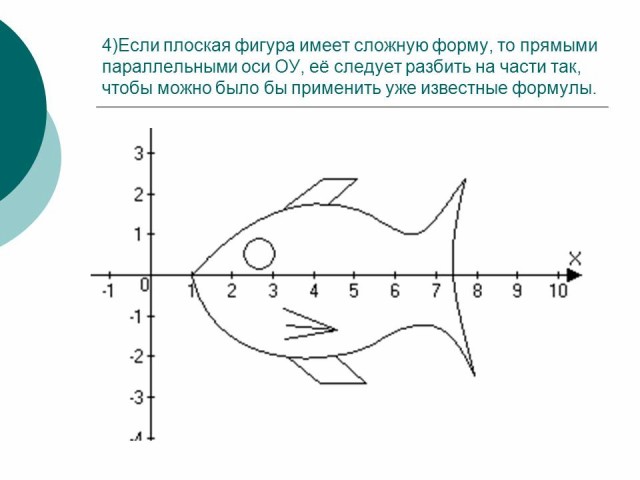
Если фигура имеет сложную форму, то прямыми , параллельными оси OY , ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.

Рисунок 3

Закрепление новых знаний:

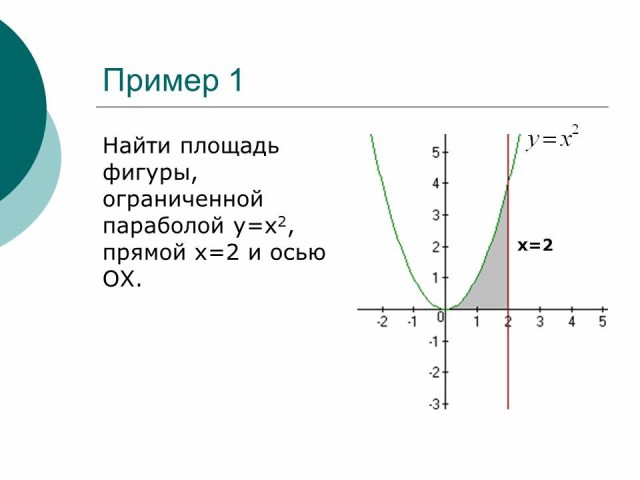
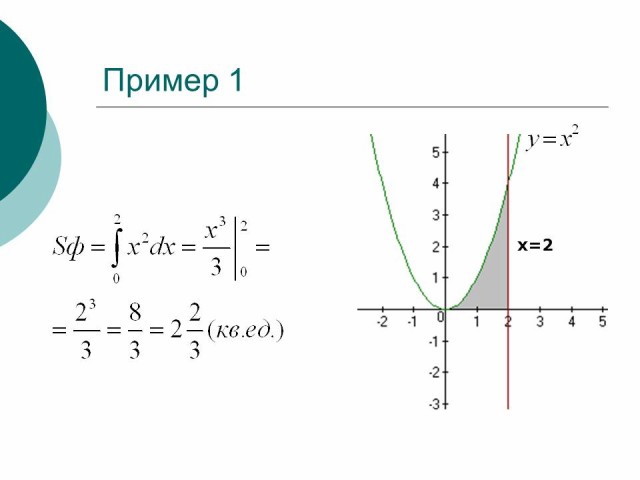
Пример 1

Найти площадь фигуры, ограниченной параболой y=x², прямой x=2 и осью OX

Рисунок 4

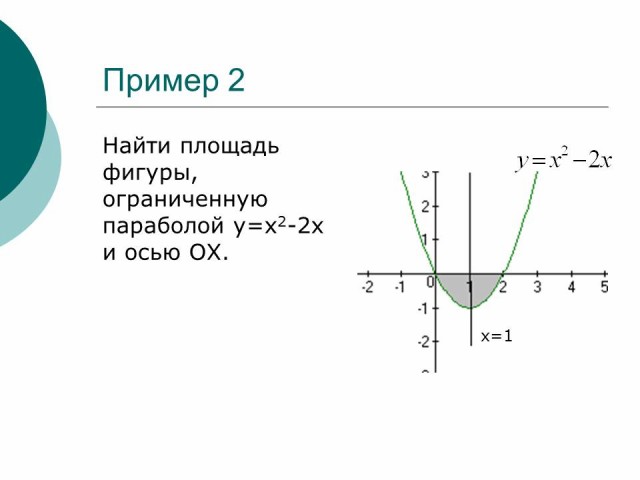
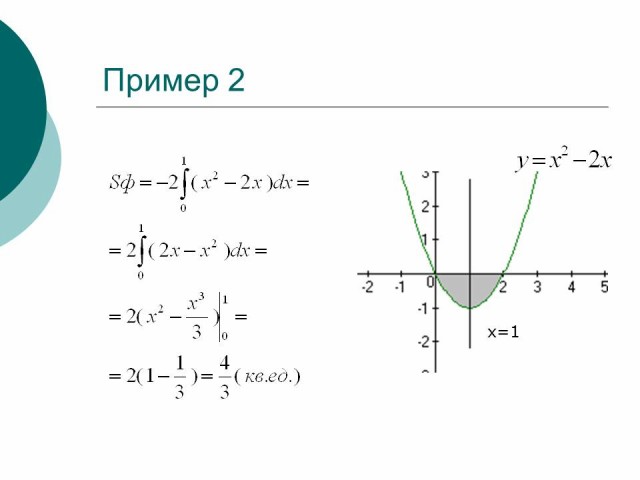
Пример 2

Найти площадь фигуры, ограниченной параболой y=x²-2x и осью OX

Рисунок 5

или т.к. парабола симметрична относительной прямой x=1, то площадь заштрихованной фигуры можно найти так:

Релаксация:

Релаксация – работа по снятию напряжения и переключению внимания (сообщения, доклады студентов)

Коротко об интеграле можно сказать так: Интеграл – это площадь

Способ вычисления площади, о котором идет речь, уходит корнями в глубокую древность. Еще в III веке до н.э. Архимед вычислил площадь параболического сегмента с помощью изобретенного им “метода исчерпывания”, который через 2 тысячи лет был преобразован в метод интегрирования.

Проверка усвоения нового материала:

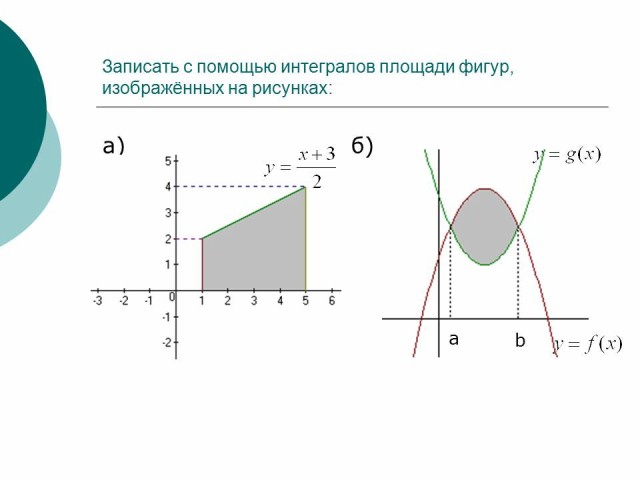
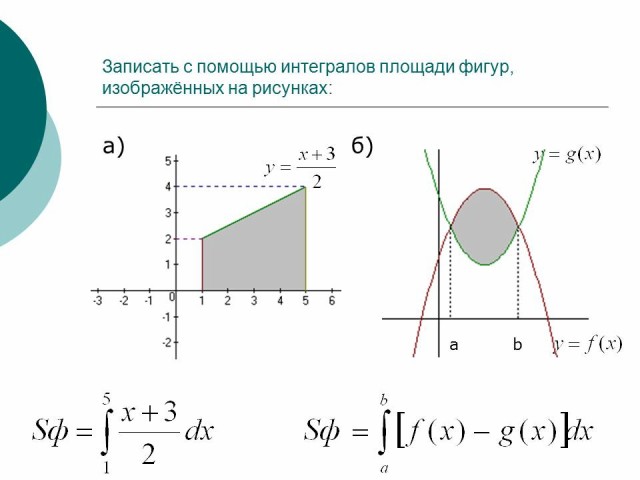
Записать с помощью интегралов площади фигур, изображенных на рисунках:

Рисунок 6

Ответ:

Рисунок 7

Ответ: