Пояснительная записка
Я применяю инновации, поэтому мои уроки построены в компетентностно-контекстной модели обучения. Поясню, как это выглядит: в ходе урока в компетентностно-контекстной модели обучения обеспечивается трансформация учебной деятельности академического типа в самостоятельную деятельность, позволяющую обучающемуся решать проблемы и задачи на основе знания о способах деятельности.
Период трансформации деятельности равен времени изучения одной темы, в рамках которой изучается целостное явление или процесс.
Единицей учебного процесса в компетентностно-контекстной модели обучения и воспитания является не урок, а тема, изучение которой осуществляется в 4 этапа.
На изучение темы “Отношения и пропорции” я отвела 14 часов.
1 этап. Деятельность академического типа (2 часа)
Проблемное изложение учебного материала. Изучаемое явление представляется целостно через ключевые определения, обобщенные алгоритмы деятельности, представляющие собой не столько содержательную, сколько функциональную сущность изучаемого явления, позволяющую использовать его как инструмент решения большого класса задач.
На данном этапе должна быть жёстко заложена структура всей темы так, чтобы чёткий порядок действий сформировался у учащихся при выполнении заданий определённого типа.
2 этап. Квазисамостоятельная деятельность (1 часа)
Это моделирующая деятельность обучающихся по поиску способов решения учебных задач и проблем с разной мерой педагогической помощи (управляемое познание). Данная форма деятельности представляет собой тренинг по овладению обучающимися умением связывать условия ситуации со знанием, объяснять необходимость выбора тех или иных способов действия и осуществлять на этой основе компетентное действие в контексте заданной учебной задачи, ситуации, проблемы.
Учащимся предлагается список заданий, в которых по приведенному выше плану и образцу рассуждения, нужно объяснить ход решения.
Один из вариантов работы на этом этапе, это обсуждение решения части задач во фронтальной беседе, а потом решения их учащимися самостоятельно. Если ошибок допускают мало, то предлагать все последующие задачи решать самостоятельно в коллективной деятельности. Если затрудняются при решении задач, план решения которых обсудили, то продолжить решение в том же режиме.
Решения данных задач создает проблемную ситуацию – состояние мыслительного взаимодействия человека с предметом познания, направленного на поиск, “открытие” и овладение новым знанием относительно научных фактов, принципов, закономерностей и условий собственного действия и поступка.
3 этап: Самостоятельная деятельность (8 часов)
Это коллективная деятельность обучающихся по решению задач и проблем в рамках изучаемой темы, набор которых очень широк: от задач, требующих прямого применения известных приемов, до исследовательских проблем. Данная форма деятельности, оставаясь учебной, фактически является формой самореализации обучающихся, позволяющей приобрести им опыт самостоятельного решения проблем на основе знания. Учитель на данном этапе – тьютор, задача которого обеспечить достижение каждым обучающимся максимально возможного результата. Уроки на данном этапе организуются таким образом, чтобы каждый ученик имел возможность работать в своем темпе, все учащиеся получают набор заданий, которые необходимо выполнить к определенному времени, одни справятся с ними раньше, другие – позже. От объема и качества выполнения заданий зависит результат деятельности каждого ученика.
4 этап: Рефлексия достигнутого результата (3 часа)
Осуществляется в форме пред итоговой и итоговой работ (контрольной работы), которые проводятся по одному классификатору. Работы задают уровень сложности освоения материала. В рамках заявленной темы он может быть различным в зависимости от уровня подготовки учащихся, но не может быть ниже уровня, заданного примерной образовательной программой основного общего образования.
I этап изучения темы в компетентностно-контекстной модели обучения.
Учебная деятельность академического типа.
Цель: формировать познавательную активность учащихся.
Развивающие задачи: развивать общеучебные умения при решении задач.
Форма обучения: коллективная.
Метод обучения: проблемное изложение.
Основные учебные практические задачи:
- образовательные (формирование познавательных УУД):
- научить в процессе реальной ситуации использовать определения следующих понятий: отношения чисел, пропорция, прямая и обратная пропорциональная зависимость; решать задачи.
- воспитательные (формирование коммуникативных и личностных УУД):
- учить слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
- развивающие (формирование регулятивных УУД)
- учить обрабатывать информацию и ранжировать ее по указанным основаниям (по видам зависимостей); представлять информацию в краткой форме, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий (видов зависимостей); учить рефлексии способов и условий действия, контролю и оценке процесса и результатов деятельности.
Ход урока
0 учебный элемент.
Орг.момент.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В математики мир отправимся смело,
В мир примеров и разных задач.
А девизом нашего урока буду такие слова:
Думать - коллективно!
Решать - оперативно!
Отвечать - доказательно!
Бороться - старательно!
И открытия нас ждут обязательно!
Мотивация урока.
При решении разнообразных практических задач часто приходится сравнивать однородные величины между собой и находить отношение величин, выраженное целым или дробным числом.
Например, скорость – это отношение пройденного пути к времени.
Географическая карта – один из важнейших документов человеческой культуры. Люди всегда рисовали уменьшенные изображения местности, причем разные участки уменьшали произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т.д.
Чтобы план местности был точным, необходимо все его детали уменьшать в одинаковое число раз с сохранением всех пропорций, т.е. делать изображение в масштабе. Поэтому каждая извилина на карте, каждый штрих, точка – результат огромного многолетнего труда землепроходцев, путешественников и исследователей.
Математика много дает для умственного развития человека – заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует помять, внимание, закаляет характер.
Надеюсь, что сегодня вы все будете работать с большим желанием узнать, что-то новое и в тоже время закрепить свои прошлые знания. Ведь как гласит народная мудрость: “Была бы охота – заладится всякая работа”.
Смогли ли вы жить в доме, в котором трубы расположены наклонно и окна разной формы?
Говорят, что в таком доме нет соразмерности, нет гармонии. Гармония (от греч, - связь, стройность) - соразмерность отдельных частей, слияние объектов в единое целое. В математике слово соразмерность определяется таким понятием как пропорция. И сегодня мы будем говорить о пропорции.
Пожалуйста, посмотрите на тему урока и определите задачи, которые мы поставим перед собой на уроке (ученики называют - узнать, что такое пропорция). Сегодня на уроке я помогу вам ответить на вопрос, что такое пропорция, а вы в свою очередь поможете ответить на мой вопрос: Как красоту и гармонию объясняет математика?
I учебный элемент.
Затем с помощью методических приемов строит работу по управлению процессом мышления.
(Использование ЭОР
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным: х/у = к.
Самым простым примером пропорциональной зависимости является запись числа как отношения двух величин.
Например, число 2 можно представить как отношение 4 и 2, 6 и 3, продолжите запись: 2 = 4/2, 6/3, .....
Задание 1. Представьте любое другое натуральное число как отношение величин. (Представляют свои варианты).
Пропорциональные величины могут быть:
Прямо пропорциональными, если их зависимость можно выразить следующим образом: у = кх, к – постоянная величина. (во сколько раз увеличивается (уменьшается) одна величина, во столько раз соответственно увеличивается (уменьшается) другая.
Обратно пропорциональными, если их зависимость можно выразить:
у = ![]() (Во
сколько раз увеличивается (уменьшается) одна
величина, во столько раз уменьшается
(увеличивается) другая.
(Во
сколько раз увеличивается (уменьшается) одна
величина, во столько раз уменьшается
(увеличивается) другая.
Ключевая задача 1. Определите прямо и обратно пропорциональные зависимости:
а = 2в, х = ![]() у =
у = ![]()
Прямая и обратная пропорциональные зависимости используются для решения задач с помощью пропорций. (Применение ЭОР
С задачами на пропорциональные величины вы знакомы, только решали их с помощью таблицы.
| В единице | Кол-во | Всего |
| ? | ||
| ? | ? |
II учебный элемент.
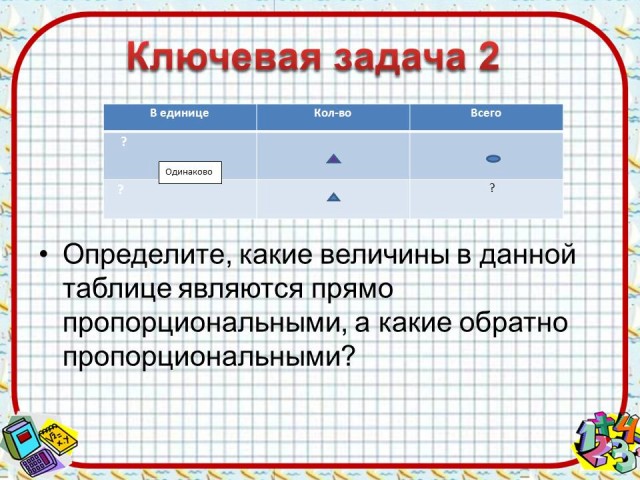
Ключевая задача 2. Определите, какие величины в данной таблице являются прямо пропорциональными, а какие обратно пропорциональными?
Решение: Нужно записать зависимость между величинами и, предполагая, что одна из величин постоянная, посмотреть, как связаны две другие.
В ед. х кол-во = всего. В данной зависимости зафиксируем, то есть примем за постоянную величину в ед., тогда кол-во и всего – прямо пропорциональные величины, аналогично связаны в ед. и всего.
Если зафиксируем всего, то можно заметить, что в ед = всего/кол-во, то есть в ед. и всего – обратно-пропорциональные зависимости.
То есть в известной задаче две величины: в 1 и количество имеют обратно пропорциональную зависимость (во сколько раз увеличивается одна, во столько раз уменьшается другая и наоборот), при этом всего имеет постоянное значение.
Зависимость же величин: в 1 и всего, и количество и всего имеют прямо пропорциональную зависимость. Во сколько увеличивается одна величина, во столько увеличивается и другая, при этом третья величина остается постоянной.
Решим задачи № 1039 и 1040 (использование ЭОР
Ключевая задача 3. Определите, какие величины являются прямо пропорциональными, а какие обратно-пропорциональными в задачах, решаемых с помощь данной таблицы: цена, кол-во, стоимость; скорость, время, расстояние; работа, мощность, время.
Решение: на основе вывода в предыдущей задачи, ответ может быть дан в зависимости от соотношения между компонентами: те, которые перемножаются для нахождения третьего – обратно пропорциональные, а каждая из них с той, которая является произведением – прямо пропорциональные.
| Ц х К=С | Ц = С/К | К = С/Ц |
| V х t=S | V=S/t | t = S/V |
| N x t = A | N = A/t | t = A/N |
И т.д.
Физкультминутка
III учебный элемент.
Эти знания мы будем использовать для решения задач с помощью пропорций. Для начала вспомним, где мы уже встречались с пропорциями?
- При решении задач на %.
- С какой зависимостью (прямой или обратной) мы имеем дело в этих задачах?
- С прямой, так как если посмотреть на таблицу, то все задачи на % сводятся к нахождению того, сколько составляет 1 %.
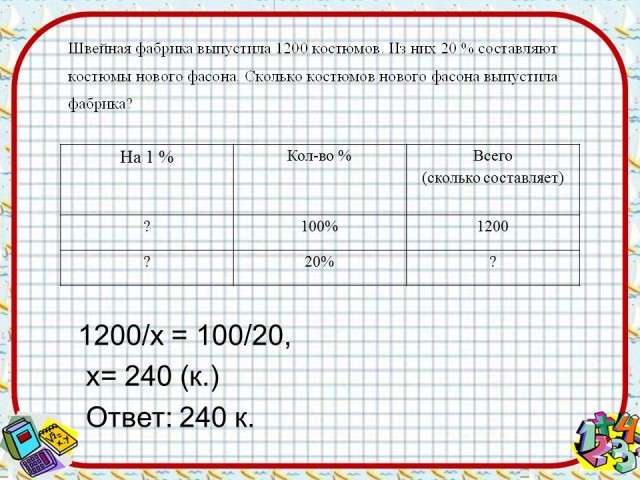
Решим задачу: Швейная фабрика выпустила 1200 костюмов. Из них 20 % составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Когда мы решали данные задачи мы не задумывались, какая перед нами зависимость, так как эту задачу мы представляли в табличной форме:
| На 1 % | Кол-во % | Всего (сколько составляет) |
| ? | 100% | 1200 |
| ? | 20% | ? |
Из таблицы видно, что нам всегда известно количество %, то есть мы ищем соотношения между количеством % и всего (сколько составляет), а между ними прямая зависимость. Составим пропорцию:
1200/х = 100/20, х= 240 (к.)
Ответ: 240 к.
Сложнее обстоит дело с другими задачами, где, составляя пропорцию, мы можем столкнуться не только с прямой, но и с обратной зависимостью величин. Прочтите алгоритм решения таких задач, его мы будем использовать для решения задач.
Алгоритм решения задач на пропорциональные величины.
- Прочитать задачу и записать краткую запись таким образом, чтобы одноименные величины были друг под другом.
- Неизвестную величину обозначить через х.
- Определить зависимость между величинами (прямо пропорциональная или обратно пропорциональная).
- Составить пропорцию: для прямой пропорциональности отношение одной величины равно отношению другой величины; для обратной пропорциональности отношение одной величины равно отношению обратной другой величины.
- Вычислить х и записать ответ.
IV учебный элемент.
Решим задачи № 1052 и 1053 с помощью пропорций
(использование ОР
http://school-collection.edu.ru/catalog/
rubr/ab9a5f35-410a-40d3-88a6-d27f37dcd725/114232/
?interface=pupilHYPERLINK
"http://school-collection.edu.ru/catalog/rubr/ab9a5f35-410a-40d3-88a6-d27f37dcd725/114232/
?interface=pupil&class=48&subject=16"&HYPERLINK
"http://school-collection.edu.ru/catalog/rubr/ab9a5f35-410a-40d3-88a6-d27f37dcd725/114232/
?interface=pupil&class=48&subject=16"class=48HYPERLINK
"http://school-collection.edu.ru/catalog/rubr/ab9a5f35-410a-40d3-88a6-d27f37dcd725/114232/
?interface=pupil&class=48&subject=16"&HYPERLINK
"http://school-collection.edu.ru/catalog/rubr/ab9a5f35-410a-40d3-88a6-d27f37dcd725/114232/
?interface=pupil&class=48&subject=16"subject=16 параграф
36.5)
V учебный элемент.
Повторение и закрепление материала: тест с применением УЛО (система контроля и мониторинга знаний Proсlass)
VI учебный элемент.
Рефлексия деятельности:
- Кому понравился новый способ решения задач?
- Какие знания необходимы для правильного решения задач, в которых говорится о прямо или обратно пропорциональных величинах?
- Назвать (по цепочке) алгоритм (эталон) решения задач по рассмотренному методу.
- В магазине “Магнит” продаются апельсины по 70 рублей за кг, а в магазине “Пятерочка” по 80 рублей. Родители вам дали 300 рублей на покупку апельсинов. Ваши действия? Объясните почему?
VII учебный элемент.
Домашнее задание: выучить теорию.