Предмет: Алгебра
Класс: 9
Раздел: Уравнения и неравенства с двумя переменными.
Тип: Урок применения полученных знаний.
Оснащение урока:
- Рабочие формулы сокращенного умножения и корней квадратного уравнения.
- Учебник Ю.Н. Макарычева. Алгебра.
- Интерактивная доска, компьютер.
- Презентация с построенными графиками для вывода общего решения и алгоритмом решения систем уравнений второй степени способом подстановки.
Методы обучения: словесный, наглядный, практический, элементы метода проектов.
Общедидактические методы: проблемный, репродуктивный, наглядно-иллюстративный, частично – поисковый.
Цель урока
- Образовательная: Закрепление полученных знаний по теме “Решение систем уравнений второй степени” аналитическим способом.
- Воспитательная: Способствовать воспитанию ответственного отношения к учебному труду и доброжелательного отношения к окружающим.
- Развивающая: Способствовать развитию интереса к математике, логического мышления и внимания решением систем уравнений.
Ход урока
| № п/п | Этапы урока | Задачи этапа |
| 1 | Организационный. | Подготовить внешнюю обстановку для работы на уроке. |
| 2 | Повторение и актуализация опорных знаний - этап подготовки учащихся к активному применению полученных знаний и умений. | Проверить полноту приобретенных знаний по данной теме графическим способом, с использованием алгоритма решения. Ликвидировать пробелы и подготовить детей к активному применению полученных знаний - самостоятельной работе. Сообщить тему, цель и задачи урока. |
| 3 | Применение, закрепление полученных знаний и умений. | Учиться решать системы уравнений второй степени аналитическим способом, корректируя ошибки самостоятельно и с помощью учителя. |
| 4 | Подведение итогов. | Объективно оценить результаты работы учащихся на всех этапах урока. |
| 5 | Сообщение домашнего задания. | Выдача разноуровневых заданий на решение систем уравнений второй степени. |
1. Организационный этап.
Подготовка внешней обстановки для работы на уроке.
2. Актуализация опорных знаний.
Вспомним:
- Какие способы решения систем уравнений второй степени мы с вами рассмотрели на предыдущих уроках? (Мы познакомились с графическим и аналитическим способами решения систем уравнений второй степени).
- Как решить систему уравнений, содержащую линейное уравнение и уравнение второй степени графическим способом?
- Какие мы должны знать формулы и теоремы для решения систем уравнений второй степени аналитическим способом?
- Что такое система уравнений, и каким знаком обозначаем систему?
К вашему вниманию подготовлены построенные графики функций, которые даны в презентации. Мы должны решить их аналитическим способом и проверить полученные ответы на готовых графиках.
- Как мы решали системы уравнений второй степени способом подстановки?
(по алгоритму (Слайд 2)).
Алгоритм решения систем уравнений второй степени способом подстановки.
- Выразим из уравнения первой степени одну переменную через другую.
- Подставим полученное выражение в уравнение второй степени. Получаем уравнение с одной переменной.
- Решим уравнение с одной переменной.
- Найдем значения второй переменной.
- Записываем ответ.
Дети сами формулируют тему урока, цели и задачи.
Тема: Решение систем уравнений второй степени с двумя переменными (Слайд 1).
Цель: Закрепить полученные знания по теме “Решение систем уравнений второй степени с двумя переменными” аналитическим способом.
Задачи: Учиться решать системы уравнений второй степени аналитическим способом, корректировать ошибки самостоятельно и с помощью учителя.
3. Этап применения, закрепления знаний и умений.
1) Решаем системы уравнений с использованием алгоритма у доски и в тетрадях.
Системы, которые были решены графически, мы будем решать аналитическим способом.
Получить в результате должны те же ответы. Если что-то не совпадает, то где-то допущена ошибка и эту ошибку общими усилиями должны найти.
Приступаем к заданиям.
Решить системы уравнений:
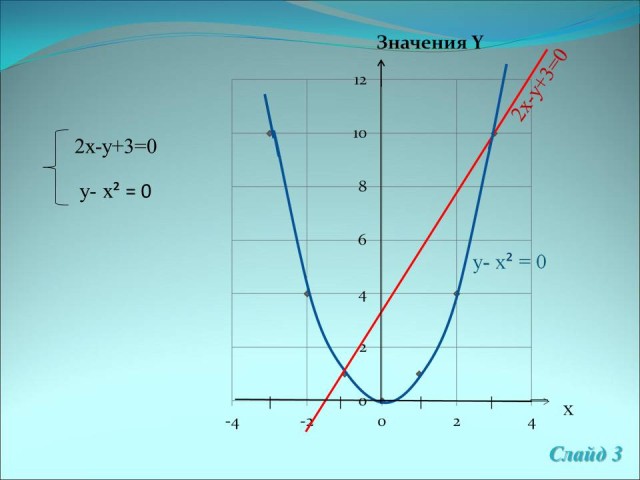
а)
Решение:
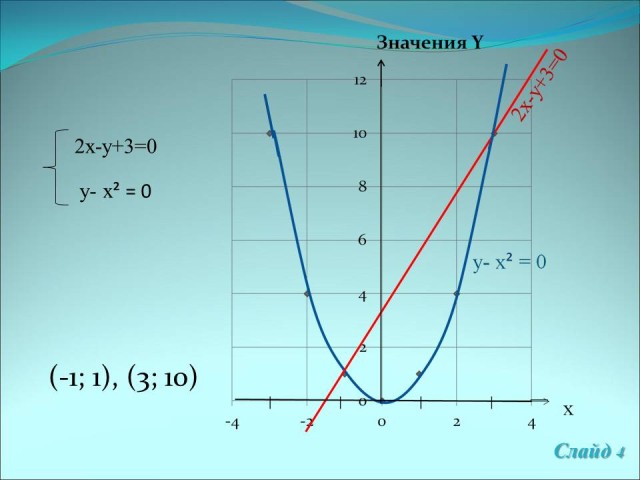
Из второго уравнения выражаем у через х, получаем у = х2, откуда методом подстановки в первое уравнение имеем -х2+2х+3=0.
Решаем приведенное квадратное уравнение х2
- 2х - 3 = 0 по теореме Виета и находим корни: ![]() 3,
3, ![]() -1, отсюда
-1, отсюда ![]() 9;
9; ![]() 1.
1.
Ответ: (3; 9), (-1; 1). (Слайд 4)
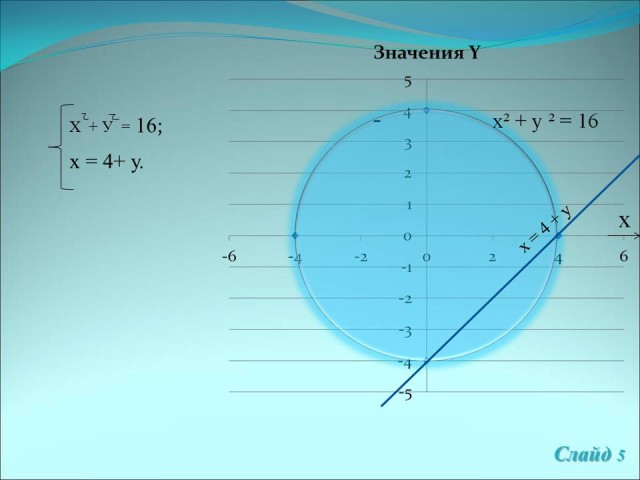
б)
Решение:
Методом подстановки вместо у = 4+ х в первое
уравнение, получаем х2 + (4 + х)2 = 16.
Применяя формулу сокращенного умножения -
квадрата суммы, получаем квадратное уравнение 2х2
+ 8х = 0. Решаем неполное квадратное уравнение 2х(х+
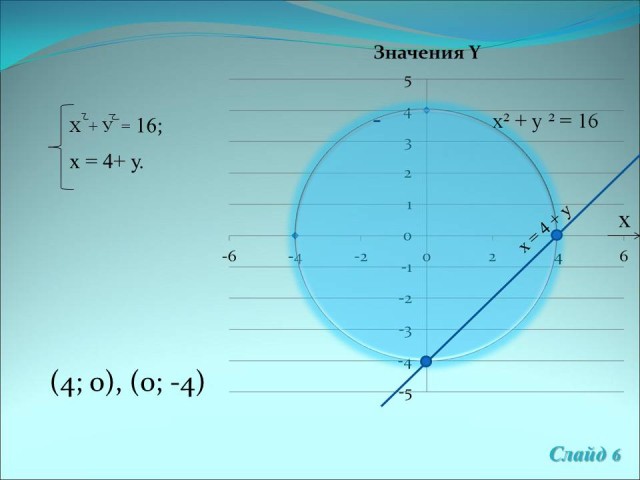
4) = 0 методом интервалов. Получаем ![]() 0;
0; ![]() -4, отсюда
-4, отсюда ![]() 4;
4; ![]() 0.
0.
Ответ: (0; 4), (-4; 0). (Слайд 6)
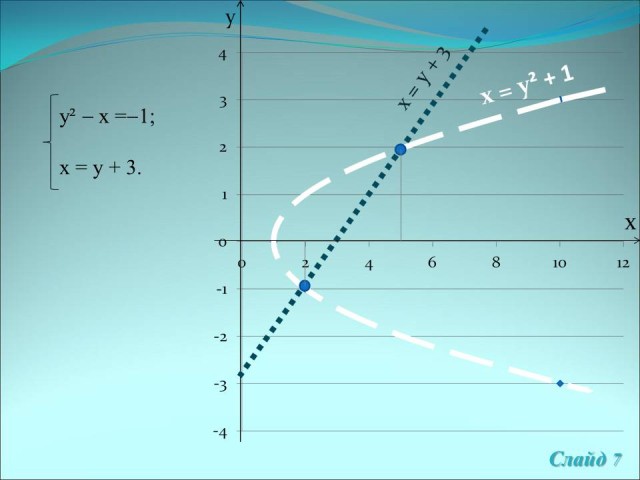
в)
Решение:
Методом подстановки в первое уравнение второго
уравнения, получаем у2 - у - 2 = 0; Решаем
приведенное квадратное уравнение по теореме
Виета. Находим корни: ![]() 2;
2; ![]() -1. Откуда
-1. Откуда ![]() 5;
5; ![]() .
.
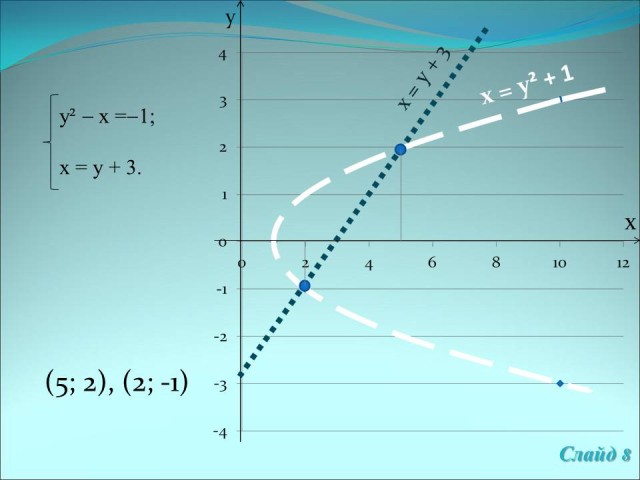
Ответ:![]() (5; 2), (2; -1). (Слайд
8)
(5; 2), (2; -1). (Слайд
8)
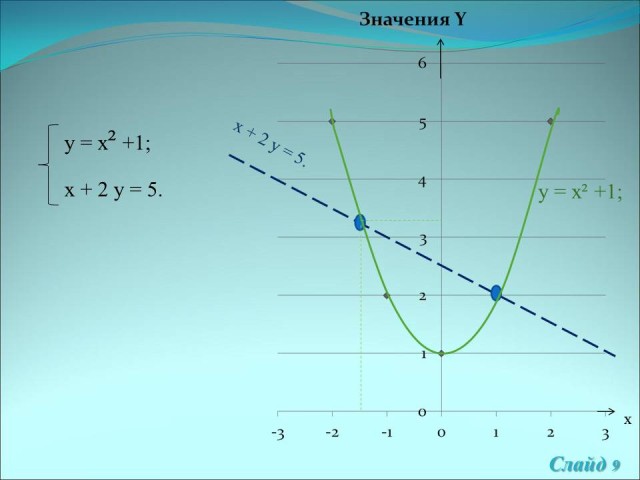
г)
Решение:
Методом подстановки во второе уравнение первого получаем 2х2 + х – 3= 0.
Решая полное квадратное уравнение с помощью
формул корней квадратного уравнения, находим ![]() 1;
1; ![]() , отсюда
, отсюда ![]() 2;
2; ![]() 3.25.
3.25.
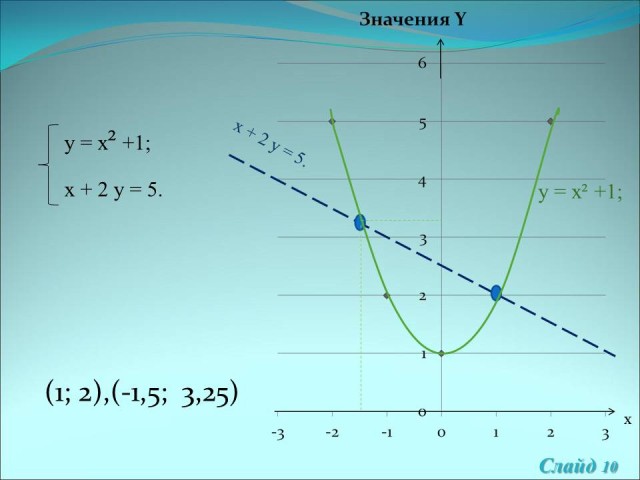
Ответ:![]() (1; 2),(-1,5;
3,25). (Слайд 10)
(1; 2),(-1,5;
3,25). (Слайд 10)
2) Самостоятельная работа.
Решите системы уравнений аналитическим и графическим способами из № 429, № 430, стр.114, параграф 7 п.19.
Рефлексия:
- Какие цели и задачи ставили перед собой на уроке?
- Смогли ли вы достичь их?
- Оцените, пожалуйста, свою деятельность на протяжении всего урока!
- Какой вид деятельности вам больше понравился?
4. Этап подведения итогов урока.
Выставление оценок.
За активную работу на уроке, учитывая ответы, как за устную, так и за письменную работу, выставляются заслуженные оценки.
5. Этап сообщения домашнего задания.
- №431, №433(а, б, в) стр.114 (легкие системы)
- №433, №443, №444 стр.114-115 (сильным ученикам)
Решите соответствующие системы уравнений аналитическим и графическим способами.