Комбинированный урок по теме «Решения квадратных неравенств». 9-й класс

Цели урока:

• Образовательная: повторить, обобщить полученные знания по теме "Квадратные неравенства"; сформировать у учащихся умение решать неравенства графическим способом.
• Воспитательная: воспитать чувства товарищества, навыков самоконтроля и взаимоконтроля, воли, упорства в достижении цели.
• Развивающая: расширение кругозора учащихся, развитие интереса к предмету, развитие личностных качеств учащихся, развитие умения самостоятельно приобретать новые знания, использование для достижения поставленной задачи уже полученные знания;

Тип урока: комбинированный

Оборудование: проектор, листы контроля, карточки.

Ход урока:

1. Организационный момент (3 мин)

Ученикам сообщается тема и цели урока.

На предыдущем уроке мы начали изучать тему: “Решение квадратных неравенств второй степени с одной переменной”, узнали алгоритм решения неравенств графическим способом. Сегодня мы продолжим учиться решать такие неравенства. Эта тема очень важна, она является ступенькой для дальнейшего обучения. Благодаря полученным умениям и навыкам в 9 классе, мы сможем успешно сдать государственную итоговую аттестацию, а также сможем решать задачи практической направленности.

Математику не зря называют “царицей наук”, ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики – любознательность. Постараемся доказать это на уроке. Вы уже умеете решать квадратные неравенства. Знание не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.

2. Фронтальная работа с классом (7 минут)

Но прежде чем приступить к решению неравенств, я бы хотела сделать устный опрос:

Вопросы:

1. Какая функция называется квадратичной?
2. Что является графиком функции y=ax²+bx+c?
3. От чего зависит направление ветвей параболы?
4. Через какую точку проходит ось симметрии параболы?
5. Как определить координаты вершины параболы?
6. Сколько корней имеет квадратное уравнение, если D>0?
7. Сколько корней имеет квадратное уравнение, если D<0?
8. Сколько корней имеет квадратное уравнение, если D=0?
9. Каков алгоритм построения графика функции y= ax²+bx+c
10. Что такое “нули функции”?

3. Решение задач на отработку навыка у доски (10 мин)

Под буквой а) решает учитель, все остальные решают учащиеся у доски.

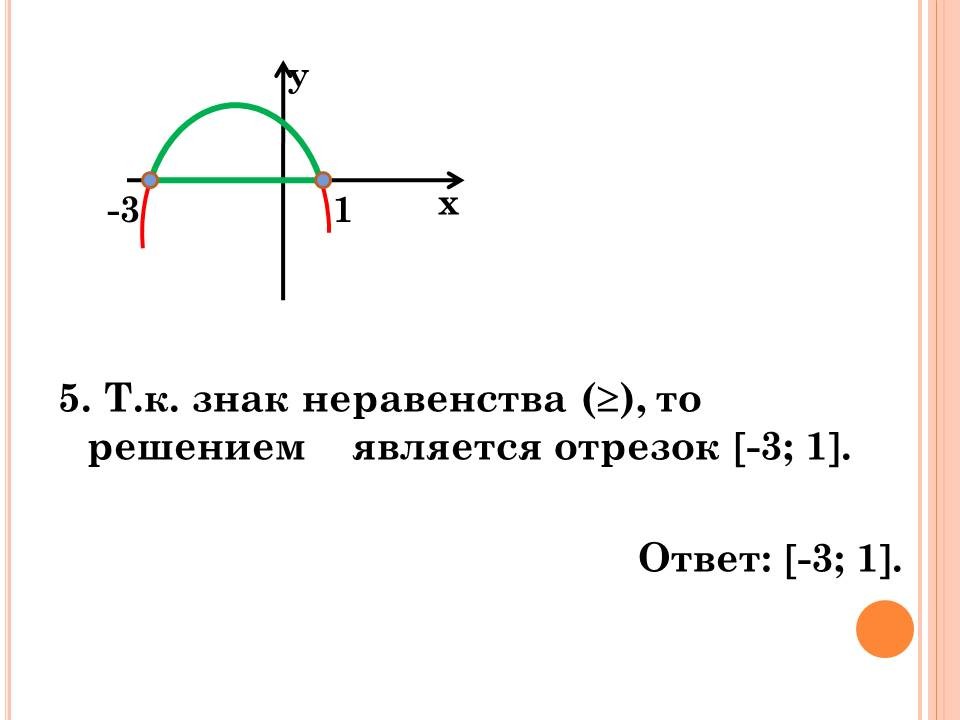
а) – x² – 2x + 3 0

б) 4x²+4x > 0

в) х² – 64 < 0

г) х² – 6х + 5 0

4. Дифференцированная самостоятельная работа в парах (20 мин)

5. Подведение итогов (3 мин)

6. Домашнее задание (2 мин)

ПРИЛОЖЕНИЕ:

Дифференцированная самостоятельная работа:

1 уровень
1 вариант	2 вариант
х2-4>0	х2-25<0
х2-8х+7 0	х2-8х+7<0
(x - 7)(x + 12) 0	(x + 6)(x - 10) 0
2 уровень
1 вариант	2 вариант
x2 < 81	x2 > 36
0,5x2 > -3x	5x2 < -15x
х2+4х - 5 0	х2-5х +4?0
(2x +1)(x + 1) 0	(3x +6)(x + 4) ?0
3 уровень
1 вариант	2 вариант
-2x2 < -18	-0,1x2 > - 6,4
3х2 - 10х +4>1	-3х2 +7х +4<-2
0,5x(10-x) 0	3x(9-x) 0
3x2 - 6x < 8 - 6x2	5x2+17x > 5x - 4

Лист контроля ученика ________________________________