Урок алгебры в 9-м классе (занятие элективного курса) по теме «Решение уравнений и неравенств, содержащих модули»

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (2 МБ)

На занятии изучается методика решения уравнений и неравенств, содержащих модули. Даётся подробная классификация уравнений и неравенств с модулем.

Введение. Определение модуля и его геометрический смысл.

«Модуль» (от лат. modulus-мера)  ввёл английский математик Р. Котес  (1682–1716). Знак модуля – немецкий математик (в 1841г.) К. Вейерштрасс (1815–1897).

Модуль числа a  есть расстояние от нуля до точки a, рис.1

Модуль разности двух чисел равен расстоянию между точками числовой прямой, соответствующим этим точкам.

рис.2

Используя определение модуля и его  геометрический смысл, можно решить простейшие уравнения и неравенства с модулем. Простейшие уравнения и неравенства удобно решать с помощью равносильных преобразований:  возведение в квадрат и т.д.

Изучение нового материала

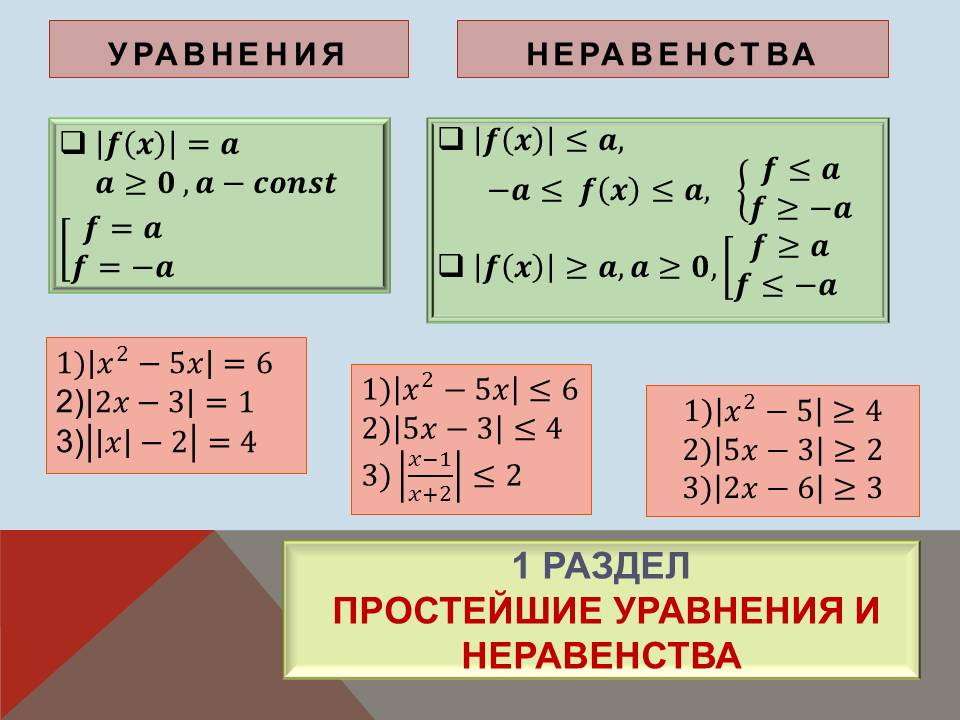
Учитель даёт систематизацию материала,  классификацию уравнений и неравенств с модулем. Показывает презентацию. Таблица №1

Таблица №1  Классификация уравнений и неравенств с модулем

 

Уравнения

  

Неравенства

1
рис.3

1
рис.5

2
рис.4

2
рис.6

3
рис.7

3
рис.9

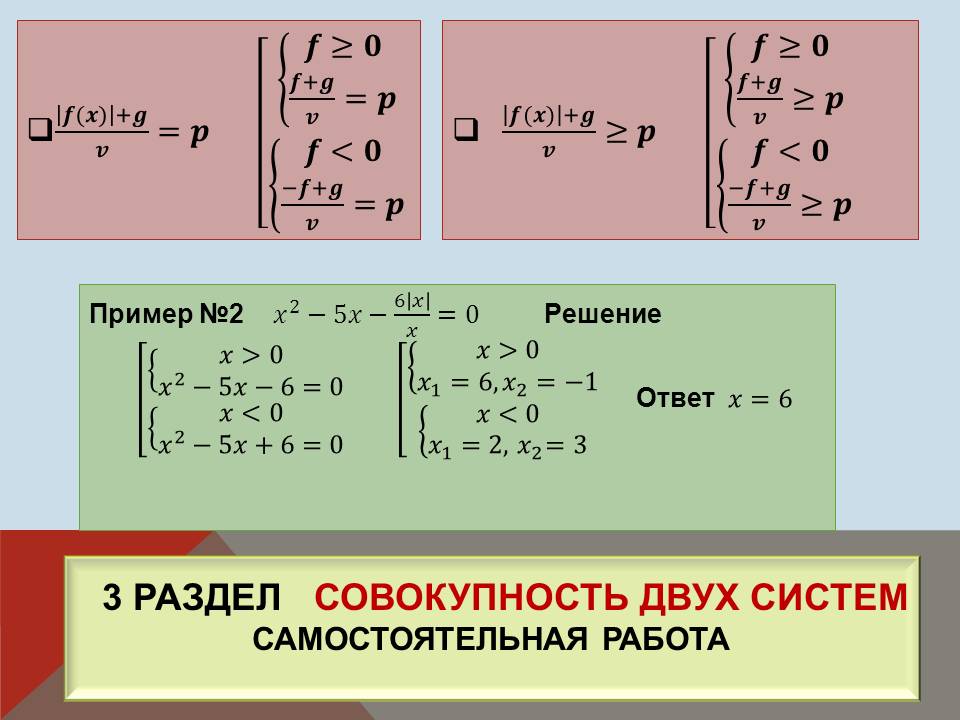
Совокупность двух систем f ≥ 0, f < 0 ,

4

Два модуля

рис.8

4

Два модуля

рис.10

5

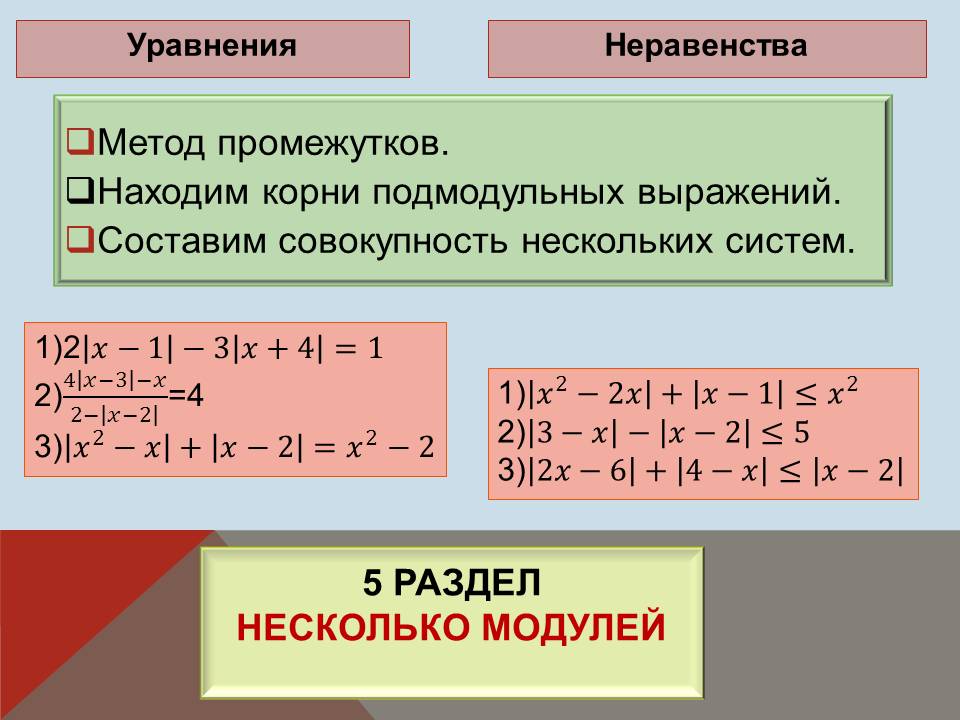
Несколько модулей.

Метод промежутков.

Находим корни подмодульных выражений.

Определим знак каждого подмодульного выражения.

Составим  совокупность нескольких систем.

6

Замена переменной.

Обозначим │f(x)│ = t, t≥ 0

Полезны формулы

рис.11

Решение примеров на закрепление

Учащиеся получают таблицу №1 (классификация уравнений и неравенств с модулем) и таблицу №2 (дидактический материал).

Таблица №2 Семинар «Решение уравнений и неравенств, содержащих модули».

 

Уравнения

 

Неравенства

1

│f(x)│ = a, a≥ 0, a – const

рис.14

1) │x2 - 5x│= 6,

2) │2x - 3│= 1,

3) ││x│- 2│= 4.

1
рис.16

рис.17

2
рис.15

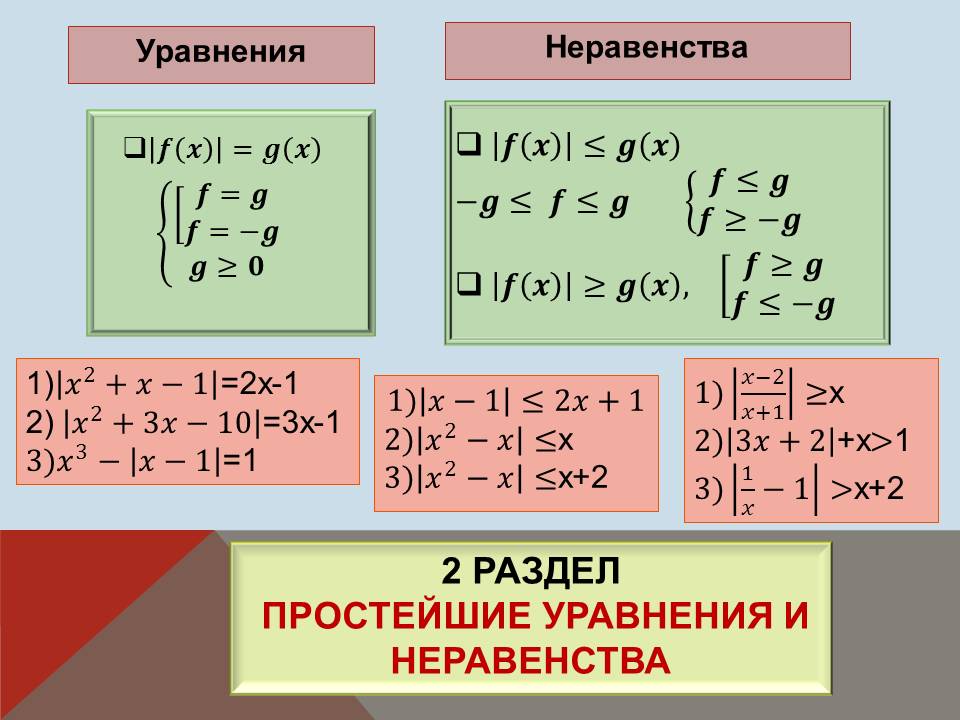
1) │x2 + x - 1│= 2x - 1,

2) │x2 + 3x - 10│= 3x - 1,

3) │x3- │x - 1││= 1.

2
рис.18

рис.19

3

Совокупность двух систем

рис.20

3

Совокупность двух систем

рис.21

4

Два модуля

рис.22

4

Два модуля

рис.23

5

Несколько модулей.

рис.24

5

Несколько модулей. Метод промежутков.

│f(x)│ ≥│g(x)│, (f - g)(f + g)≥ 0

1) │x2 - 2x│+ │x - 1│≤ x2,

2) │3 - x│- │x - 2│≤ 51,

3) │2x - 6│+ │4 - x│≤ │x - 2│.
6

Замена переменной.

│f(x)│ = t, t ≥ 0, f2 = t2

1) (x - 2)2 - 8│x - 2│+ 15 = 0,

2) x2 + │x│- 6 = 0,

3) x2 - 2x - 5│x - 1│+ 5 = 0.

 6

Замена переменной.

рис.25

1) x2 - │x│- 12 ≥ 0,

2) 20 - 3x2 + 11│x │> 0,

3) x2 - 2x + 1 < 2│x - 1│.

Примеры №1 из каждого раздела подготовленные ученики (консультанты) показывают решение с помощью презентации. Примеры №2 все учащиеся решают самостоятельно, консультанты проверяют и помогают (периодически демонстрируются слайды с решениями). Примеры №3 – домашнее задание.

1 раздел. Простейшие уравнения и неравенства с модулем.

рис.261 ученик. Пример №1. │x2 - 5x│ = 6

рис.27

Пример №2. │2x - 3│= 1    (учащиеся решают самостоятельно).

рис.28

2 ученик. Пример №1. │x2 - 5x│ ≤ 6     

рис.12

Ответ [-1;2] U [3;6]

Пример №2. │5x - 3│ ≤ 4  (учащиеся решают самостоятельно).

Решение. -4  ≤ 5x - 3 ≤ 4, -1  ≤ 5x ≤ 4, -0,2  ≤ x ≤ 1,4,

Ответ [-0,2;1,4]

рис.13 3 ученик. Пример №1. │x2 - 5│ ≥ 4

рис.29

Ответ (-∞;-3] U [-1;1] U [3; +∞)

Пример №2. │5x - 3│≥ 2 (учащиеся решают самостоятельно).

рис.30

Ответ (-∞;0,2] U [1; +∞)

2 раздел.

рис.314 ученик. Пример №1. │x2 + x - 1│= 2x - 1, x ≥ 0,5

рис.32

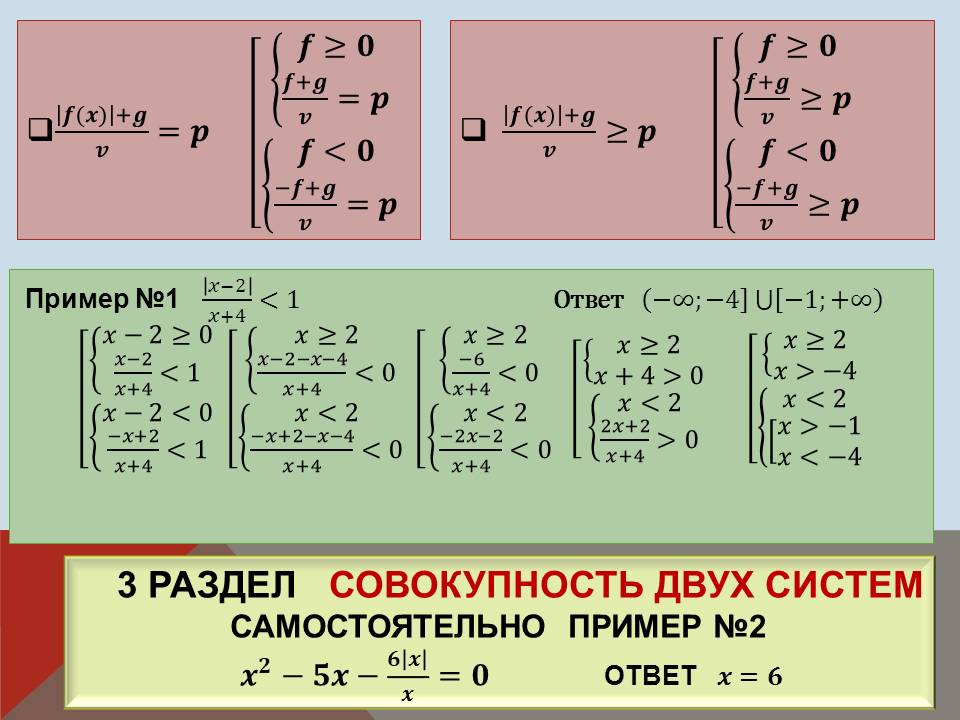
3 раздел. Совокупность двух систем.

5 ученик. Пример №1. рис.33

рис.34

Ответ (-∞;-4] U [-1; +∞)

Пример №2. рис.35 (учащиеся решают самостоятельно).

рис.36

4 раздел.  Два модуля

рис.376 ученик. Пример №1. │-x2 + x - 1│= │-x2 + 2x + 3│,

рис.38

Ответ {-4; 2; -0,5}

рис.39 7 ученик. Пример №1.  │x + x2 - 3│≤ │x - 2 + 2x2│

Решение. (x + x2 - 3 + x - 2 + 2x2)(x + x2 - 3 - x + 2 - 2x2) ≤ 0

(2x + 3x2 - 5)(-x2 - 1) ≤ 0, (2x + 3x2 - 5)(x2 + 1) ≥ 0, (2x + 3x2 - 5) ≥ 0

рис.40

Пример №2. │3x - 1│< │2x - 5│ (учащиеся решают самостоятельно).

(3x - 1 + 2x - 5) (3x - 1 - 2x + 5) < 0, (5x - 6)(x + 4) < 0, -4 < x < 1,2

Ответ (-4; 1,2)

5 раздел. Несколько модулей. Метод промежутков.

8 ученик. Пример №1. 2│x - 1│- 3│x + 4│= 1

Решение. x1 = 1, x2 = -4

рис.41

9 ученик. Пример №1. │ x2 - 2x│+ │x - 1│≤ x2

Решение. │ (x - 2)x│+ │x - 1│≤ x2

x1 = 0, x2 = 2, x3 = 1

рис.42

6 раздел. Замена переменной.

рис.43 10 ученик. Пример №1 (x - 2)2 - 8│x -2│+ 15 = 0

Решение.  │x -2│= t, t >0

рис.44

Ответ {-3; -1; 5; 7}

Пример №2. x2 + │x │- 6 = 0 (учащиеся решают самостоятельно).

Решение.  │x │= t, t >0

t2 + t - 6 = 0, t1 = -3, t2 = 2, │x │= 2, x1 = -2, x2 = 2

Ответ  x1 = -2, x2 = 2

11 ученик. Пример №1. x2 -│x │- 12 ≥ 0

Решение.  │x │= t, t >0

рис.45

Домашнее задание.

Примеры №3 (1-6 разделы).