Основы логики. Логические операции
Скачать презентацию (1.77 МБ)
Цели:
- оказание помощи учащимся при решении задач, где необходимо построение таблиц истинности, применение логических операций в простых и сложных выражениях;
- оказание помощи учащимся при подготовке к ЕГЭ;
- оказание помощи учителю при организации подготовки учащихся к ЕГЭ.
Задачи:
- отработать навыки по формированию представления об истории возникновения и эволюции логического мышления;
- отработать навыки составления однозначной интерпретации произвольной информации на основе алгебры логики;
- совершенствовать навыки формирования информационной культуры и потребности в приобретении знаний;
- совершенствовать навыки самостоятельной работы.
Тип урока: Данный урок подходит как для изучения нового материала, так и для закрепления изученного.
Ход урока:
1. Организационный момент. Приветствие учащихся.
2. Теоретический материал: изучение, повторение
Историческая справка. Логика - это очень древняя наука.

Основы формальной логики заложил ученый Древней Греции - Аристотель (384 г.-322 г. до н.э.) . Заслуга ученого состоит в том, что он отделил форму мышления от содержания, попытался соединить логику и математику, разработал раздел теории доказательств.

Немецкий ученый Лейбниц (1646-1716) взглянул на логику Аристотеля через призму математики. Им написан трактат - "Азбука мыслей", сжатый и краткий язык символов. Лейбниц разработал идею логического исчисления. Рассуждения обозначил буквами, сложные высказывания - формулами. В результате удалось содержательные рассуждения заменить формальными вычислениями.

Джордж Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику. Буль - автор известных произведений, в т.ч. работы "Математический анализ логики"(1847г.). Основной труд Джорджа Буля - "Исследование законов мысли", в котором представлен раздел логики - алгебра высказываний.
Логика - это наука о формах и способах мышления.
Основными формами мышления являются
- понятие,
- высказывание,
- умозаключение.
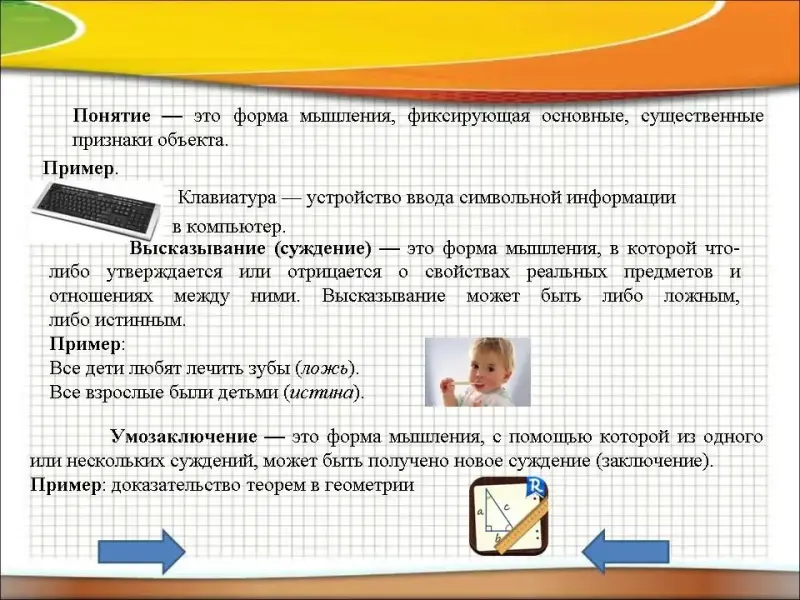
Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.
Пример. Клавиатура - устройство ввода символьной информации в компьютер.

Высказывание (суждение) - это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо ложным, либо истинным.
Пример: Все дети любят лечить зубы (ложь).

Все взрослые были детьми (истина).
Умозаключение - это форма мышления, с помощью которой из одного или нескольких суждений, может быть получено новое суждение (заключение).

Пример: доказательство теорем в геометрии.
Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: "истина" (1) и "ложь" (0).
Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок "и", "или", "не".
Логическое отрицание (инверсия)
Присоединение частицы "не" к высказыванию называется операцией логического отрицания или инверсией.
Обозначение: ¬.
На естественном языке: неверно, что..., не
Пример.
А - "Сегодня идет снег"
¬ А - "Неверно, что сегодня идет снег" или "Сегодня не идет снег"
Таблица истинности логического отрицания
А ¬ А 0 1 1 0
Инверсия высказывания истинна, если высказывание ложно, и ложна, когда высказывание истинно.
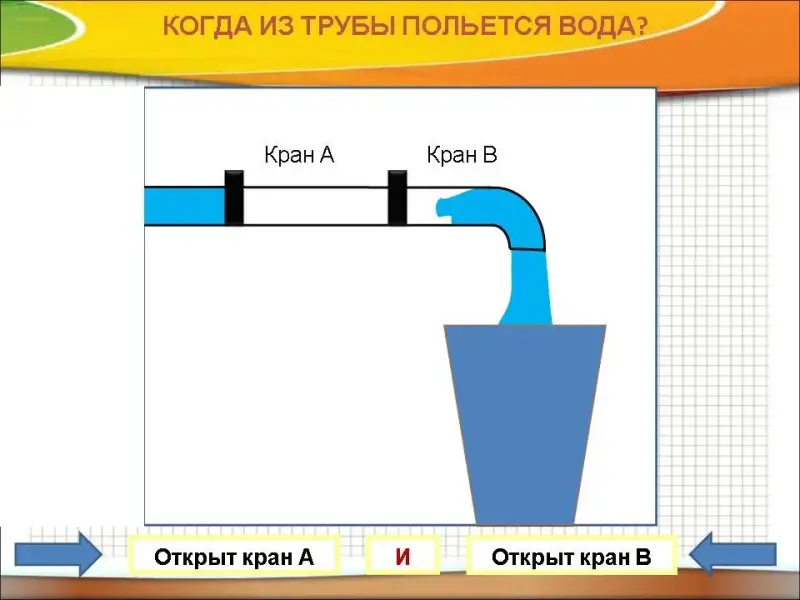
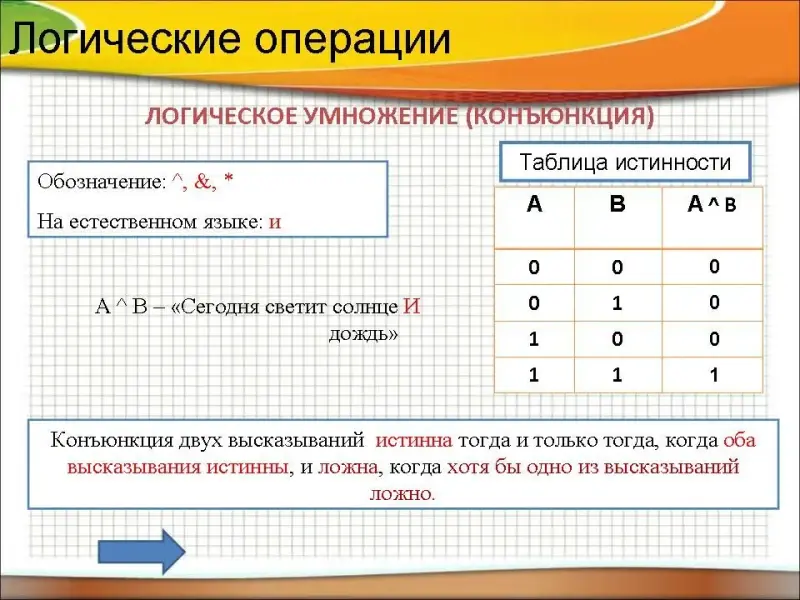
Логическое умножение (конъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза "и" называется операцией логического умножения или конъюнкцией.
Обозначение: ^, &, *
На естественном языке: И.
Пример. А ^ B - "Сегодня светит солнце И дождь"
Таблица истинности логического умножения
А В А ^ B 0 0 0 0 1 0 1 0 0 1 1 1
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно из высказываний ложно.
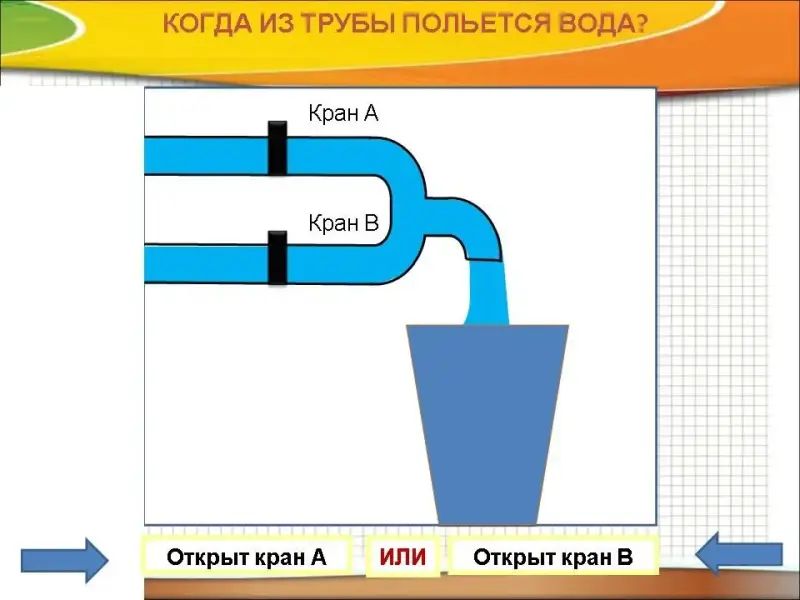
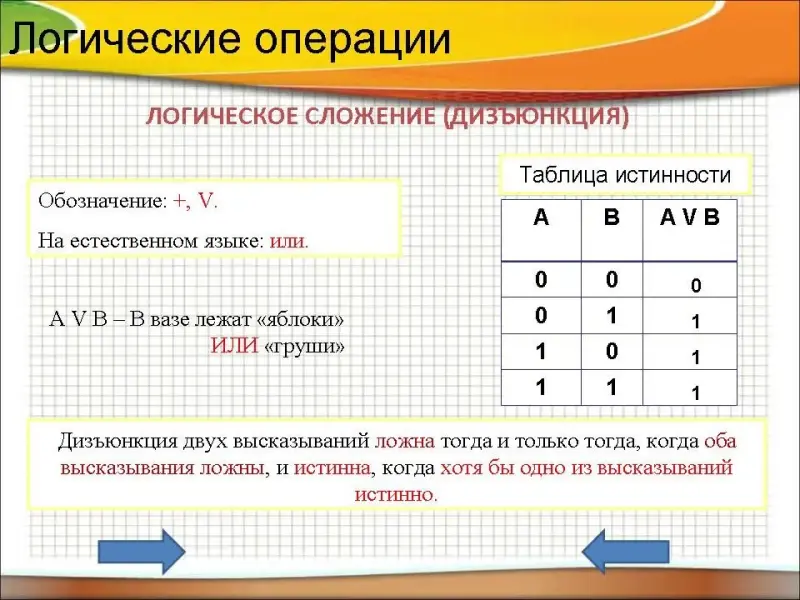
Логическое сложение (дизъюнкция)
Объединение двух (или нескольких) высказываний с помощью союза "или" называется операцией логического сложения или дизъюнкцией.
Обозначение: +, V.
На естественном языке: ИЛИ.
Пример. А V B - В вазе лежат "яблоки" ИЛИ "груши"
Таблица истинности логического сложения
А В А V B 0 0 0 0 1 1 1 0 1 1 1 1
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно из высказываний истинно.
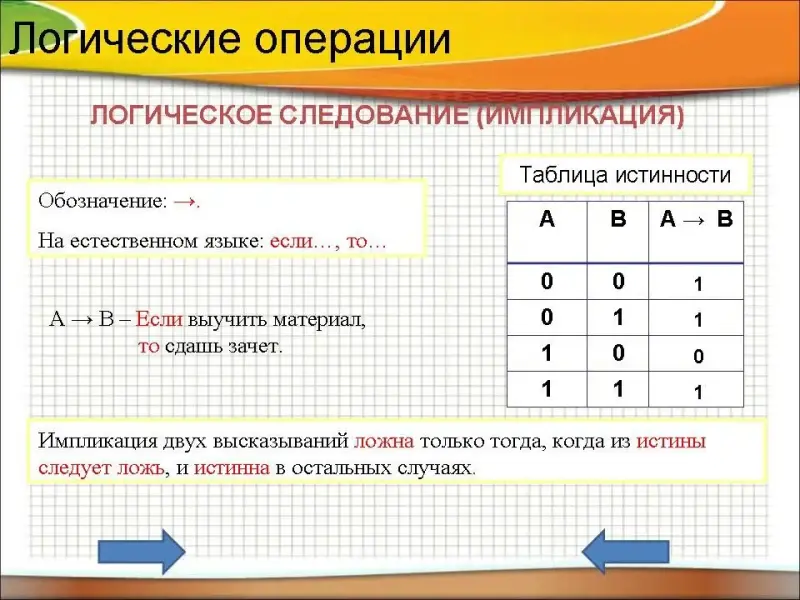
Логическое следование (импликация)
Обозначение: ->.
На естественном языке: если..., то...
Пример. А -> B - Если выучить материал, то сдашь зачет.
Таблица истинности логического следования
А В А -> B 0 0 1 0 1 1 1 0 0 1 1 1
Импликация двух высказываний ложна только тогда, когда из истины следует ложь, и истинна в остальных случаях.
Логическое равенство (эквивалентность)
Обозначение: ![]() , <->, =.
, <->, =.
На естественном языке: тогда и только тогда, когда
Пример. А ![]() B - Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий.
B - Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий.
Таблица истинности логического равенства
А В А <-> B 0 0 1 0 1 0 1 0 0 1 1 1
Эквивалентность двух высказываний истина только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Порядок выполнения логических операций в сложном логическом выражении:
- Инверсия ¬;
- Конъюнкция ^;
- Дизъюнкция V;
- Импликация >;
- Эквивалентность
 .
.
Для изменения указанного порядка выполнения логических операций используются скобки.
3. Практическая работа.
Учащиеся выполняют задания. (презентация, слайды 17-23). После выполнения задания учащиеся проверяют правильность решения.
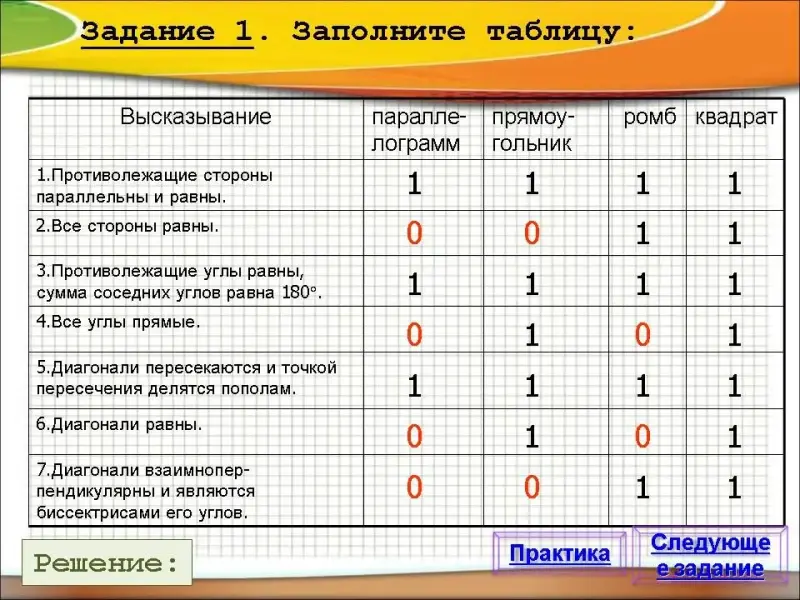
Задание 1: Заполните таблицу. Истина - 1, Ложь - 0
| Высказывание | параллелограмм | прямоугольник | ромб | квадрат |
| Противолежащие стороны параллельны и равны. | ||||
| Все стороны равны. | ||||
| Противолежащие углы равны, сумма соседних углов равна 180° . | ||||
| Все углы прямые. | ||||
| Диагонали пересекаются и точкой пересечения делятся пополам. | ||||
| Диагонали равны. | ||||
| Диагонали взаимно перпендикулярны и являются биссектрисами его углов. |
Задание 2: Запишите высказывание "если яблоко зеленое или мелкое, то оно твердое", используя знаки логических операций.
Задание 3: Определите результат логического выражения при заданных параметрах
¬( ¬B & ¬C ) U ¬( ¬A & ¬C ), при А=1, В=1, С=0.
Задание 4: Для какого имени истинно высказывание:
(Первая буква гласная) /\ (Четвёртая буква согласная) \/ (B слове четыре буквы)?
1) СЕРГЕЙ
2) АЛЕКСЕЙ
3) АНТОН
4) ИЛЬЯ
Задание 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
Какое выражение соответствует F?
1) (X ^ Y) ? (X ![]() Z)
Z)
2) (X ^ Y) ? (X ![]() Z)
Z)
3) (¬Х ^ Y) ? (X ![]() Z)
Z)
4) ¬(X ^ Y) ? (X ![]() Z)
Z)
4. Итоги урока. Вопросы учеников.
5. Домашнее задание. Учить конспект, придумать аналогичные задания.
6. Подведение итогов урока
Анализ и оценка успешности достижения цели занятия. Определение перспективы последующей работы.