Изопроцессы. 10-й класс
Скачать презентацию (1.95 МБ)
Тип урока: урок изучения и первичного закрепления новых знаний.
Цель:
- Формирование представления об изопроцессах, изучение законов Бойля-Мариотта, Гей-Люссака, Шарля, их графическое представление.
- Расширить кругозор учащихся осуществлением межпредметных связей с курсом математики
- Создать условия для выявления качества и уровня овладения знаниями и умениями с использованием компьютерных технологий.
Задачи:
- Образовательные: изучить газовые законы; формировать умение объяснять законы с молекулярной точки зрения; изображать графики процессов; начать обучение учащихся решать графические и аналитические задачи, используя уравнение состояния и газовые законы; установление межпредметных связей (физика, математика, биология).
- Воспитательные: продолжить формирование познавательного интереса учащихся; в целях интернационального воспитания обратить внимание учащихся, что физика развивается благодаря работам ученых различных стран и исторических времен; продолжить формирование стремления к глубокому усвоения теоретических знаний через решение задач.
- Развивающие: активизация мыслительной деятельности (способом сопоставления), формирование алгоритмического мышления; развитие умений сравнивать, выявлять закономерности, обобщать, логически мыслить; научить применять полученные знания в нестандартных ситуациях для решения графических и аналитических задач.
План урока:
- Организационный момент.
- Актуализация знаний.
- Объяснение нового материала.
- Закрепление нового материала.
- Домашнее задание.
Ход урока
I. Организационный момент.
Слайды 1-3
Перед учащимися определяются цели урока, освещается ход урока и конечные результаты его проведения.
II. Актуализация знаний.
Фронтальный опрос
- Что является объектом изучения МКТ? (Идеальный газ.)
- Что в МКТ называется идеальным газом? (Идеальный газ - это газ, в котором взаимодействием между молекулами можно пренебречь.)
- Для того чтобы описать состояние идеального газа, используют три термодинамических параметра. Какие? (Давление, объем и температура.)
- Какое уравнение связывает между собой все три термодинамических параметра? (Уравнение состояния идеального газа).
III. Объяснение нового материала.
Слайды 4-6
Учитель. Итак, мы отметили, что уравнение состояния идеального газа связывает между собой три макроскопических параметра: р, Т и V. Но при любых ли процессах все эти параметры изменяются? Давайте рассмотрим несколько примеров. Возьмем надувной круг. Какой параметр здесь постоянен? (учащиеся отвечают: объем не изменяется). А если мы деформируем его и объем изменим, но внешних условий менять не будем? (учащиеся отвечают: при деформации объем уменьшится, давление внутри возрастет, а температура останется постоянной). А что произойдет с кругом при повышении температуры? (учащиеся отвечают: объем растет с повышением температуры, а давление внутри круга равно внешнему давлению и постоянно). Теперь мы знаем, что существуют процессы, при которых отдельные макроскопические параметры сохраняются.
Теперь рассмотрим каждый из представленных процессов подробнее и установим для каждого из них связь между Т, р и V.
Количественные зависимости между двумя параметрами газа одной и той же массы при неизменном значении третьего параметра называют газовыми законами.
Изопроцесс - процесс, при котором масса газа и один из его термодинамических параметров остаются неизменными.
Газовых законов, как и изопроцессов - три. Используя уравнение состояния идеального газа, можно вывести все три закона за 10 минут. Но в истории физики эти открытия были сделаны в обратном порядке: сначала экспериментально были получены газовые законы, и только потом они были обобщены в уравнение состояния. Этот путь занял почти 200 лет: первый газовый закон был получен в 1662 году Бойлем и Мариоттом, уравнение состояния - в 1834 году Клапейроном, а более общая форма уравнения - в 1874 году Д.И. Менделеевым.
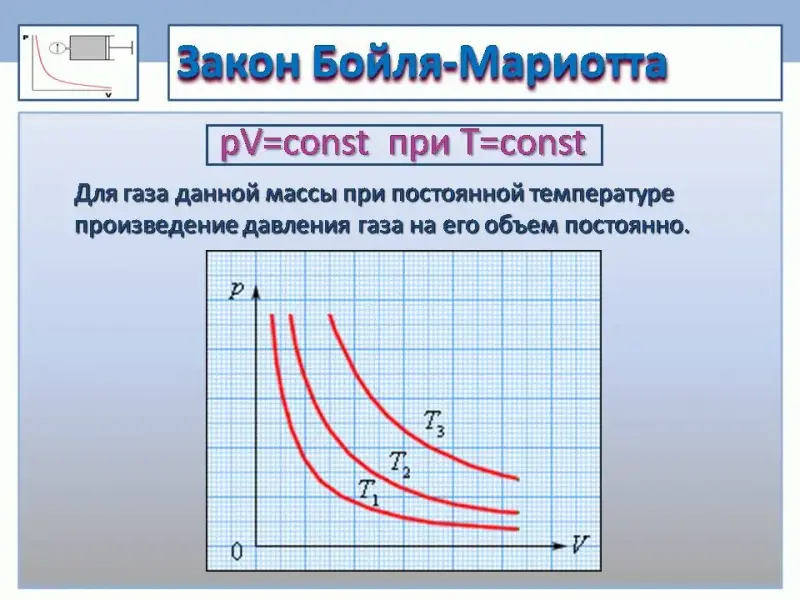
Слайды 7-10 Изотермический процесс. Закон Бойля-Мариотта.
Первый газовый закон был открыт английским ученым Бойлем в 1662 году. Работа называлась «Новые эксперименты, касающиеся воздушной пружины». Бойль изучал давление газа в зависимости от объёма при постоянной температуре. Данный процесс называется изотермическим.
Имя французского аббата Эдма Мариотта в названии закона появилось в 1676 году благодаря его работе "Речь о природе воздуха", в которой были описаны опыты, аналогичные экспериментам Бойля. Поэтому закон получил название закона Бойля-Мариотта.

Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.
Затем рисуется график, даётся его название - изотерма. При построении графиков проводится аналогия с соответствующим разделом из математики.

Закон Бойля-Мариотта справедлив для любых газов, а так же и для их смесей, например, для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Изотермическим можно приближенно считать процесс медленного сжатия воздуха или расширения газа под поршнем насоса при откачке его из сосуда. Правда температура газа при этом меняется, но в первом приближении этим изменением можно пренебречь.
Однако газовые законы активно работают не только в технике, но и в живой природе, широко применяются в медицине.
Закон Бойля-Мариотта начинает «работать на человека» (как, впрочем, и на любое млекопитающее) с момента его рождения, с первого самостоятельного вздоха.
При дыхании межреберные мышцы и диафрагма периодически изменяют объем грудной клетки. Когда грудная клетка расширяется, давление воздуха в легких падает ниже атмосферного, т.е. «срабатывает» изотермический закон (pV=const), и вследствие образовавшегося перепада давлений происходит вдох. Другими словами воздух идет из окружающей среды в легкие самотеком до тех пор, пока величины давления в легких и в окружающей среде не выравниваются.
Выдох происходит аналогично: вследствие уменьшения объема легких давление воздуха в них становится больше, чем внешнее атмосферное, и за счет обратного перепада давлений он переходит наружу.
Слайды 11-14
Закрепление нового материала. Решение задач.
Слайды 15-18 Изобарный процесс. Закон Гей-Люссака.
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным. Первооткрыватель - Жозеф Луи Гей-Люссак (1802 год).

Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.
Рисуется график, даётся его название и отмечается, что зависимость (V/T) представляет собой tg угла наклона прямой к оси T.

Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.
Слайды 19, 12-14
Закрепление нового материала. Решение задач.
Слайды 20-23 Изохорный процесс. Закон Гей-Люссака.
В 1787 году французский ученый Жак Шарль измерял давление различных газов при нагревании при постоянном объеме и установил линейную зависимость давления от температуры, но не опубликовал исследования. Через 15 лет к таким же результатам пришел и Гей-Люссак и, будучи на редкость благородным, настоял, чтобы закон назывался в честь Шарля.

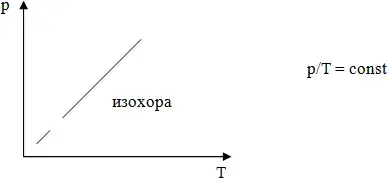
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Рисуется график, даётся его название.
Изохорным можно считать увеличение давления газа в любой емкости или в электрической лампочке при нагревании.
Слайды 24, 12-14
Закрепление нового материала. Решение задач.
IV. Закрепление нового материала.
Слайды 25-31
Мы познакомились с тремя изопроцессами: изотермическим, изобарным и изохорным. Все они вытекают из уравнения состояния идеального газа.
Далее предлагаю обучающимся мини тест, чтобы они определились в своих знаниях полученных за урок, а также проверили свои умения.
V. Домашнее задание.
Слайды 32
§69, № 522, № 524
Литература:
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский Физика, 10 класс. - М.: «Просвещение», 2011.
- А.П. Рымкевич Физика. Задачник 10-11 класс. - М.: Дрофа, 2005.