Уроки алгебры и начала анализа по теме "Нахождение наибольшего и наименьшего значения функции на отрезке на примерах заданий вариантов ЕГЭ". 11-й класс
Образовательные задачи урока.
- повторить необходимые и достаточные условия существования точек экстремума, понятия: стационарные и критические точки;
- ввести алгоритм нахождения наибольшего и наименьшего значения функции на отрезке
- сформировать умение решать задачи на нахождение наибольшего и наименьшего значения степенной функции на отрезке с помощью производной.
- разобрать прототипы задач № 1 В14 экзаменационной работы в формате ЕГЭ.
- Продолжить формирование общеучебных умений и навыков: навыков самоконтроля, умения писать необходимом темпе.
Воспитательные задачи:
- cодействовать в ходе урока формированию основных мировоззренческих идей (материальность мира, познаваемость мира и его закономерностей, обусловленность развития науки потребностям производства);
- cодействовать воспитанию у учащихся таких нравственных качеств, как коллективизм;
- cодействовать профилактике утомляемости школьников, используя разнообразные виды работы на уроке.
I. Организационный момент. Приветствие. Проверка готовности класса к уроку. Выявление отсутствующих.
II. Актуализация знаний учащихся.
Повторить с учащимися основные понятия прошлых уроков: точки экстремума, каково достаточное условие точек экстремума, стационарные точки и критические точки (учащихся отвечают с места)
Повторить таблицу производных основных функций и основные правила нахождения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III. Изучение нового материала.
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке
(учащиеся записывают себе в тетрадь).
Пусть функция ![]() непрерывна и дифференцируема на отрезке
непрерывна и дифференцируема на отрезке ![]() , то для
нахождения наибольшего и наименьшего значения функции на отрезке нужно:
, то для
нахождения наибольшего и наименьшего значения функции на отрезке нужно:
- найти производную функции, найти стационарные точки (решаем уравнение, приравнивая производную к нулю)
- среди полученных стационарных точек выбрать те, которые принадлежат отрезку

- найти значение в стационарных точках и в концах отрезка, то есть
 и
и  .
. - среди полученных значений выбрать наибольшее или наименьшее.
Записать схему нахождения наибольшего и наименьшего значения функции на отрезке в тетради (учитель оформляет схему на доске):
Пусть![]() непрерывна на
непрерывна на ![]() и дифференцируема. Тогда, для нахождения
и дифференцируема. Тогда, для нахождения
![]() или
или ![]() :
:
- Находим



 находим
находим 
- Проверяем принадлежность
 отрезку
отрезку 
- Находим
 ,
,  ,
,  .
. - Среди полученных значений выбираем
 или
или 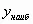 .
. - Записываем ответ (Акцентировать внимание, что в ответе должно быть записано либо целое число, либо конечная десятичная дробь).
Пример № 1. Найти наименьшее значение функции ![]() на отрезке
на отрезке ![]() . (Учитель совместно с учащимися записывает решение на доске последовательно проговаривая каждый пункт алгоритма).
. (Учитель совместно с учащимися записывает решение на доске последовательно проговаривая каждый пункт алгоритма).
Решение:
![]()
![]()
![]()

Ответ: ![]()
Пример № 2. Найти наибольшее значение функции ![]() на отрезке
на отрезке ![]()
Решение:
![]()
![]()
![]()
![]()
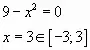

Ответ: 23
Пример № 3. Найдите наименьшее значение функции ![]() на отрезке
на отрезке ![]() .
.
Решение:
![]()
![]()
![]()

Ответ: -3
Пример № 4. Найдите наибольшее значение функции ![]() на отрезке
на отрезке ![]() .
.
Решение:
Упростим функцию ![]()



![]()
Ответ: 1
IV. Закрепление материала.
- Найдите наименьшее значение функции
 на отрезке
на отрезке 
- Найдите наименьшее значение функции
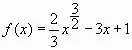 на отрезке
на отрезке 
- Найдите наименьшее значение функции
 на отрезке
на отрезке 
V. Итоги урока.
- Повторить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.
- Выставить отметки за урок.
VI. Домашнее задание:
- Найдите наименьшее значение функции
 на отрезке
на отрезке 
- Найдите наибольшее значение функции
 на отрезке
на отрезке 
- Найдите наибольшее значение функции
 на отрезке
на отрезке 
- Найдите наименьшее значение функции
 на отрезке
на отрезке 
- Найти наибольшее значение функции
 на отрезке
на отрезке 
Урок № 2. "Нахождение наибольшего и наименьшего значения функций ![]() и
и ![]() на отрезке
на отрезке ![]() .
.
Тип урока: комбинированный.
Образовательные задачи:
- обеспечить повторение в ходе урока алгоритма нахождения наибольшего и наименьшего значения функции на отрезке;
- продолжить формирования навыка применения этого алгоритма при решении второго типа задач экзаменационных вариантов ЕГЭ;
- продолжить формирование общеучебных умений и навыков: навыков самоконтроля, умения в необходимом темпе читать и писать, анализировать условия задачи.
Воспитательные задачи:
- содействовать в ходе урока формированию основных мировоззренческих идей (материальность мира, познаваемость мира и его закономерностей, обусловленность развития науки потребностям производства);
- содействовать воспитанию у учащихся таких нравственных качеств, как коллективизм. умение слушать товарищей;
- содействовать профилактике утомляемости школьников.
I. Организационный момент.Приветствие. Проверка готовности класса к уроку. Выявление отсутствующих.
II. Проверка домашнего задания. Фронтальная проверка домашнего задания. Если у большинства учащихся возникли вопросы, разобрать на доске решение конкретного задания, если лишь у некоторых, объяснить в индивидуальном порядке, предварительно схематично обговорив решение у доски.
III. Актуализация знаний. Повторить еще раз алгоритм нахождения наибольшего и наименьшего значения функции на отрезке с оформлением схемы на доске.
Повторить следующие формулы для дальнейшего изучения материала:
![]() ,
, ![]() ,
, ![]()
Решить на повторение примеры (1 учащийся пишет решение на доске с комментариями по решению, остальные записывают себе в тетради).
IV. Решение новых прототипов задач (разбирает решение учитель)
Пример № 1. Найти наименьшее значение функции ![]() на отрезке
на отрезке ![]()
Решение
![]()
![]()
![]()

Ответ: -1
Пример № 2. Найти наименьшее значение функции ![]() на отрезке
на отрезке ![]()
Решение. Преобразуем и упростим функцию ![]() , используя свойство логарифмов
, используя свойство логарифмов ![]()




Ответ: -6
V. Закрепление материала (самостоятельное решение задач учащимися у доски).
Пример № 3. Найти наибольшее значение функции ![]() на отрезке
на отрезке ![]()
Решение.

Ответ: 51
Пример № 4. Найти наименьшее значение функции ![]() на отрезке
на отрезке ![]()
Решение.
![]()


(![]() , так как
, так как ![]() )
)

![]()
Ответ: 4
Пример № 5. Найти наименьшее значение функции ![]() на отрезке
на отрезке ![]()
Решение
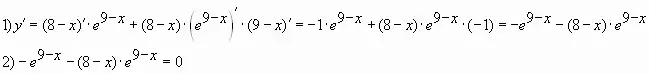

Ответ: -1
Пример № 6. Найти наибольшее значение функции ![]() на отрезке
на отрезке ![]()
Решение:



![]()
![]()

Ответ: 1
Пример № 7: Найдите наибольшее значение функции ![]() на отрезке
на отрезке ![]()
Решение



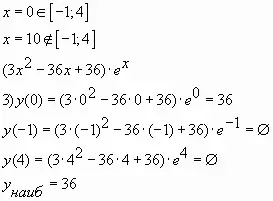
Ответ: 36
VI. Итоги урока.
- Повторить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.
- Проговорить основные алгоритмы решения тех примеров, которые изучены на уроке.
VII. Домашнее задание по вариантам.
| 1 вариант | 2 вариант |
| Найти наибольшее значение функции |
Найти наибольшее значение функции |
| Найдите наибольшее значение функции |
Найдите наибольшее значение функции |
| Найдите наименьшее значение функции |
Найдите наименьшее значение функции |
| Найдите наименьшее значение функции |
Найдите наименьшее значение функции |
| Найдите наибольшее значение функции |
Найдите наибольшее значение функции |
| Найдите наибольшее значение функции |
Найдите наибольшее значение функции |
| Найдите наибольшее значение функции |
Найдите наибольшее значение функции |