На интегрированных уроках наиболее эффективно формируются метапредметные умения как основа целостного мировоззрения. В рамках методического объединения математических дисциплин (математика, физика, информатика, графика) в ГБОУ СОШ № 549 данный вид уроков системно реализуется более 10 лет. Особое внимание уделяется формированию умений создавать обобщения, устанавливать аналогии, применять модели и схемы одной дисциплины для решения учебных и познавательных задач другого предмета. Применение программы “КОМПАС” дает возможность формировать и развивать компетентности в области использования информационно-коммуникационных технологий в процессе интегрированного урока, избегать инструментальной погрешности при построениях. Интеграция “геометрия-графика-информатика” продуктивно реализуется при изучении темы “Сечения”, что позволяет устранить дублирование простейшего материала; с полной отдачей использовать лимит времени; устранить возможные противоречия в трактовке понятий и использовать готовое содержание из другой дисциплины; продемонстрировать более широкое поле использования изучаемого понятия; реализовать проблемную методику обучения предмету.
Представленная разработка может быть использована как на уроке объяснения нового материала по геометрии (так как в ней графически акцентирован каждый из этапов решения задач при оптимальном времени появления нового факта), так и на уроке применения предметных знаний (в качестве самопроверки с образцом)
Оборудование:
- ПК или ноутбуки;
- Проектор и экран или интерактивная доска;
- Файл с исходным заданием или задание на печатной основе
Тема: вычисление площади сечения.
Этапы и ход урока
1. Организационный момент.
Учитель математики:
На уроках информатики, графики и геометрии мы уже отработали способы построения плоских сечений многогранников. Покажем примеры использования при решении стереометрических задач планиметрических фактов и графических методов.
2. Актуализация знаний.
3. Формирование умений, навыков
Учитель математики:
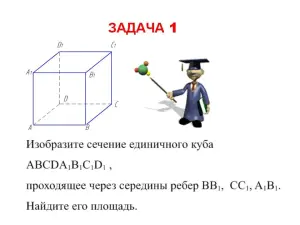
Задача 1. Изобразите сечение единичного куба ABCDA1B1C1D1 , проходящее через середины ребер BB1, CC1, A1B1. Найдите его площадь.
Приложение 1 (видео)
Приложение 2 (видео)
Приложение 3 (видео)
Учитель графики:
Сначала повторим примитивы, которые понадобятся для построения сечения (видеоролик 1-2) Выполним чертеж для данной задачи с использованием графического редактора КОМПАС.
Введем обозначения K – середина BB1, N – середина CC1, E – середина A1B1. Построим сечение и выделим его заливкой (видеоролик 1-3)
Учитель математики:
Оформим решение задачи в тетради (слайды 2-4).
Учитель математики:
Задача 2. Изобразите сечение правильной четырехугольной пирамиды SABCD, проходящее через вершины А, В и середину ребра SC. Все ребра пирамиды равны 1. Найдите его площадь.
Учитель графики:
Выполним чертеж для данной задачи с использованием графического редактора КОМПАС.
Введем обозначения М – середина SC. Построим сечение методом вспомогательных секущих плоскостей. Выделим полученное сечение заливкой (видеоролик 1-4).
Учитель математики:
Оформим решение задачи в тетради (слайды 7-12).
5. Подведение итогов. Рефлексия.