Урок информатики в 9-м классе. Тема: "Системы счисления"

Тип урока: Урок изучения новой темы.

Дидактическая цель: создать условия для актуализации и закрепления учебной информации

Цель урока:

Образовательная:

• знакомство с понятием «система счисления»;
• умение различать виды систем счисления и применять их на практическом занятии;
• умение правильно записывать числа в системах счисления;
• формирование способности для применения правил перевода чисел из одной системы счисления в другие.

Развивающая:

• развивать логическое мышление, умение обобщать, конкретизировать;
• формирование внимания, умения наблюдать и закреплять знания;

Воспитательная:

• воспитывать самостоятельность, уважительное отношение друг к друг;
• воспитание информационной культуры учащихся.

Методы обучения: наглядный, информационно-развивающий, опрос.

Формы организации познавательной деятельности: индивидуальная.

Средства обучения: учебник Семакина “Информатика и ИКТ. 9 класс. ” учебник для 9 класса общеобразовательных учреждений, рабочие тетради, авторучки, проектор, компьютер, компьютерная презентация по теме урока.

План урока:

1. Организационный момент.
2. Изучение нового материала.
3. Физкультминутка.
4. Формирование умений, навыков.
5. Домашнее задание

Ход урока

1. Организационный момент.

Приветствие, проверка присутствующих. Мы сегодня начинаем изучение новой темы. Данная тема очень важна. Хотелось бы отметить умение решать задачи на систему счисления дает возможность набрать более высокие баллы, что очень важно при сдаче ЕГЭ и поступлении в ВУЗЫ. Открываем тетрадки, записываем сегодняшнее число и тему: СИСТЕМЫ СЧИСЛЕНИЯ.

План темы

1. Историческая справка
2. Определение системы счисления
3. Виды системы счисления
4. Правила перевода чисел из одной системы счисления в другую

2. Объяснение нового материала (по плану, приложение 3)

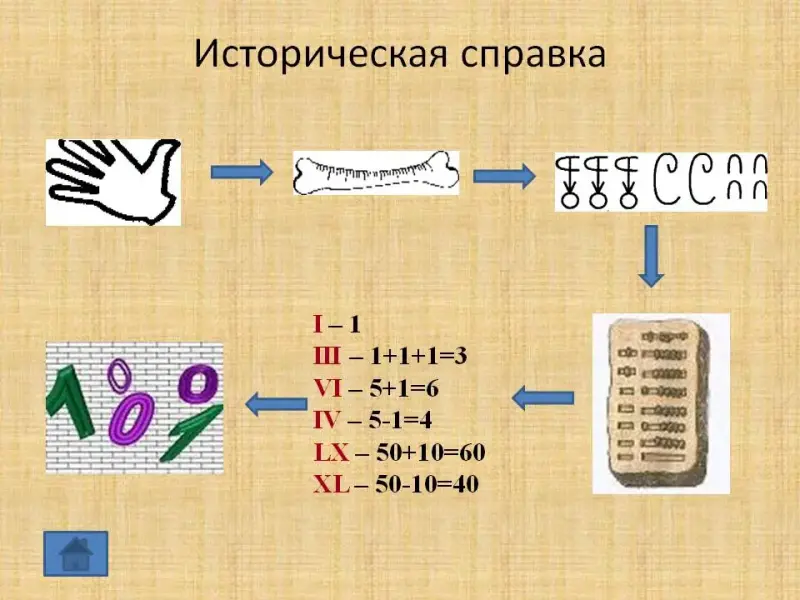
2.1. Историческая справка

Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.

Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 3 246: 

Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие - палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления

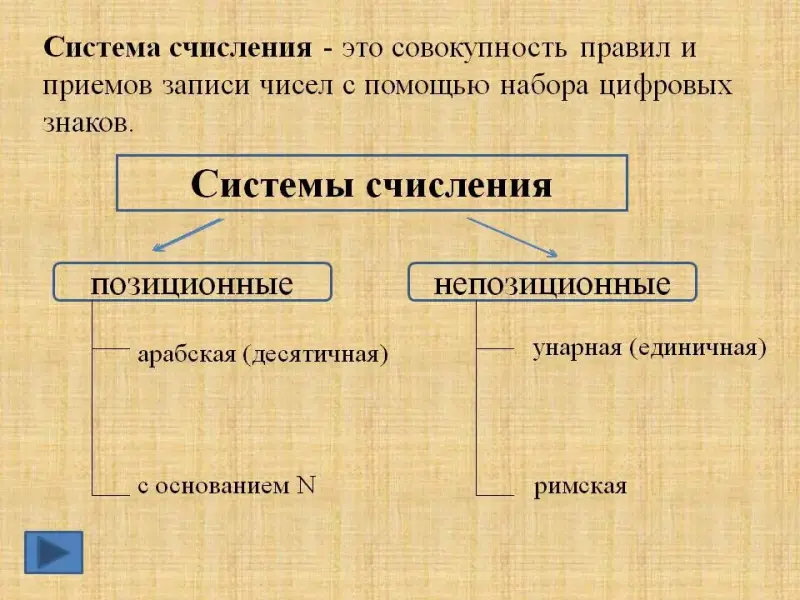
2.2. Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.

• позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
• непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.

Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.

Таблица 1. Запись чисел в римской системе счисления

Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.

Мы с вами более подробно рассмотрим позиционные системы счисления.

В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.

Алфавитом системы счисления называется совокупность всех цифр.

Количество цифр, необходимых для записи числа в системе, называют основанием  системы счисления. Основание системы записывается в справа числа в нижнем индексе: 78₁₀, 1100010₁₂, AF12₁₆ и т. д.

Количество цифр, составляющих алфавит, называется его мощностью.

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен. Разряд - номер позиции в числе. Нумеруются справа налево, начиная с нуля.

Пример. Число6184₁₀ запишется в форме многочлена следующим образом:

6184₁₀ = 6*10 ³ +1*10 ² +8*10 ¹ +4*10 ⁰

2.3. Виды систем счисления.

В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.

Десятичная система счисления – в настоящее время наиболее известная и используемая. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 - углов нет, 1 - один угол, 2 - два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции

Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.

Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.

В вычислительных машинах используется двоичная система счисления, её основание - число 2. Для записи чисел в этой системе используют только две цифры - 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII - ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.

Учащиеся заполняют таблицу в тетрадях (приложение 1, таблица 1).

2.4. Правила перевода чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Числа 10100110₂ , 703₈ , 23FA1₁₆ перевести в десятичную систему счисления.

10100110₂=1*2⁷+0*2⁶+1*2⁵+0*2⁴+0*2³+1*2²+1*2¹+0*2⁰=128+32+4+2=166₁₀

703₈=7*8²+0*8¹+3*8⁰=448+3=447₁₀

23FA1₁₆=2*16⁴+3*16³+15*16²+10*16¹+1*16⁰=131072+12288+3840+160+1=147361

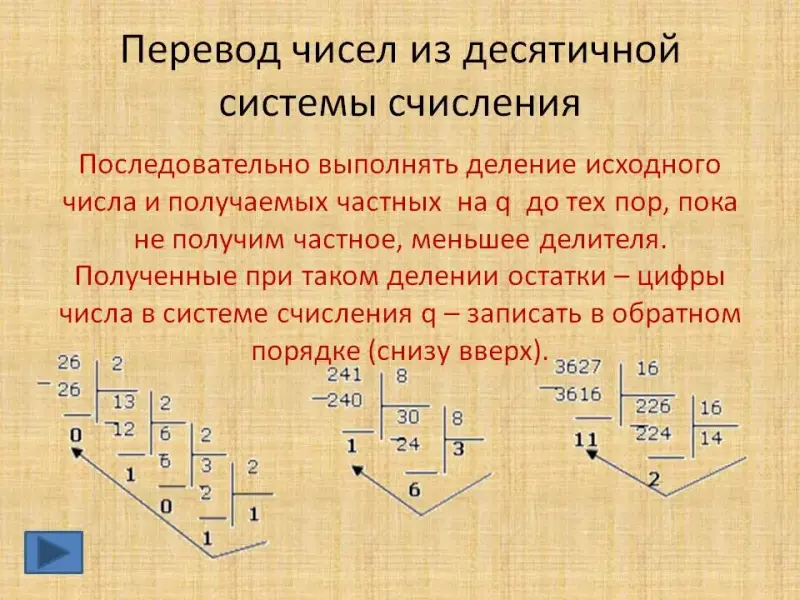
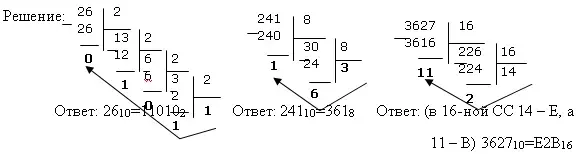
2. Правило перевода из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).

Пример. Перевести числа из десятичной системы счисления

3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (табл.).

Число 10010110111₂ перевести в восьмеричную и в шестнадцатеричную системы счисления.

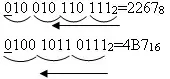
4. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).

Числа 726₈ и 74С₁₆ перевести в двоичную систему счисления.

726₈= 111 010 110₂

74С₁₆ = 0111 0100 1100₂ (при записи числа первый 0 не пишется)

5. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Число FAE₁₆ перевести в восьмеричную систему счисления.

FAE₁₆=111110101110₂

111 110 101 110₂=7656₈

Число 635₈ перевести в шестнадцатеричную систему счисления.

635₈ =110011101₂

1 1001 1101₂=19D₁₆

3. Физкультминутка (см. презентация 2)

4. Формирование умений и навыков

Работа с вопросником. Отвечают устно на вопросы, используя свой конспект.

5. Домашнее задание (приложение 4)

• Учить конспект, прочитать §16 по учебнику.
• Написать дату своего дня рождения в римской системе счисления.

Подведение итогов урока.

Анализ и оценка успешности достижения цели занятия. Определение перспективы последующей работы.

Приложение 2