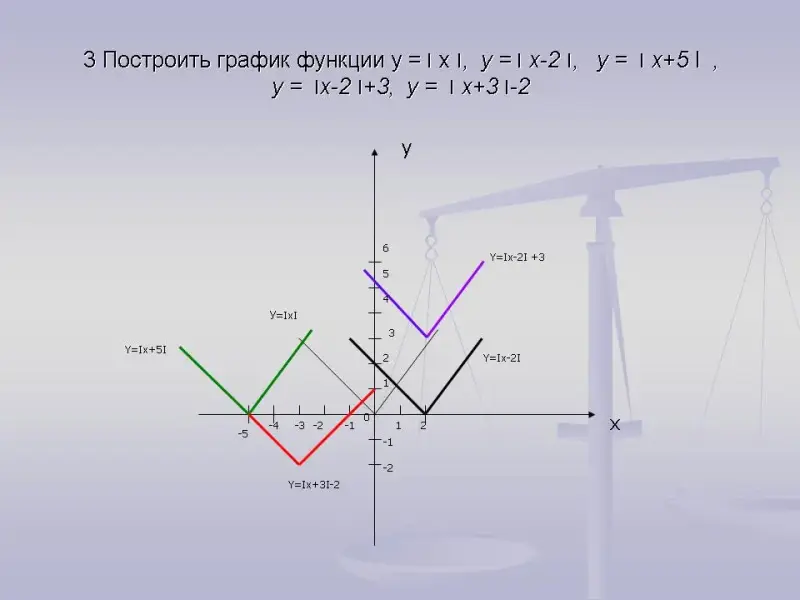
Решение уравнений с модулями и параметрами
Скачать презентацию (433.66 КБ)
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные: научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие: развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные: воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
ХОД УРОКА
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a, если a > 0, число - a, если a < 0, нуль, если a = 0. Или
| | a | ={ | a, если a > 0 |
| 0, если a = 0 | |
| - a, если a < 0 |
Из определения следует, что | a | > 0 и | a | > a для всех a € R .
Неравенство | x | < a, (если a > 0) равносильно двойному неравенству - a < х < a.
Неравенство | x | < a, (если a < 0) не имеет смысла, так как | х | >0.
Неравенство | x | > a, (если a > 0) равносильно двум неравенствам
Неравенство | x | > a, (если a < 0) справедливо для любого х € R.
2) «Решение уравнений с параметрами»
Решить уравнение с параметрами - значит указать, при каких значениях параметров существуют решения и каковы они.
а) определить множество допустимых значений неизвестного и параметров;
б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.
2. Устные упражнения
1. Решить уравнение | x - 2 | = 5; Ответ: 7; - 3
| x - 2 | = - 5; Ответ: решения нет
| x - 2 | = х + 5; Ответ: решения нет; 1,5
| x - 2 | = | x + 5 |; Ответ: решения нет; - 1,5; решения нет; - 1,5;
2. Решить уравнение: | x + 3 | + | y - 2 | = 4;
Расcмотрим четыре случая
1.
| { | x + 3 > 0 | { | x > - 3 |
| y - 2 > 0 | y > 2 | ||
| x + 3 + y - 2 = 4 | y = - x + 3 |
2.
| { | x + 3 > 0 | { | x > - 3 |
| y - 2 < 0 | y < 2 | ||
| x + 3 - y + 2 = 4 | y = x + 1 |
3.
| { | x + 3 < 0 | { | x < - 3 |
| y + 2 > 0 | y > - 2 | ||
| - x - 3 - y - 2 = 4 | y = x + 9 |
4.
| { | x + 3 < 0 | { | x < - 3 |
| y + 2 < 0 | y < - 2 | ||
| - x - 3 - y - 2 = 4 | y = - x - 9 |
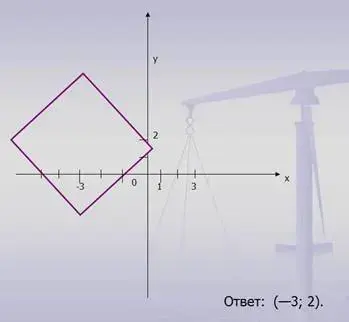
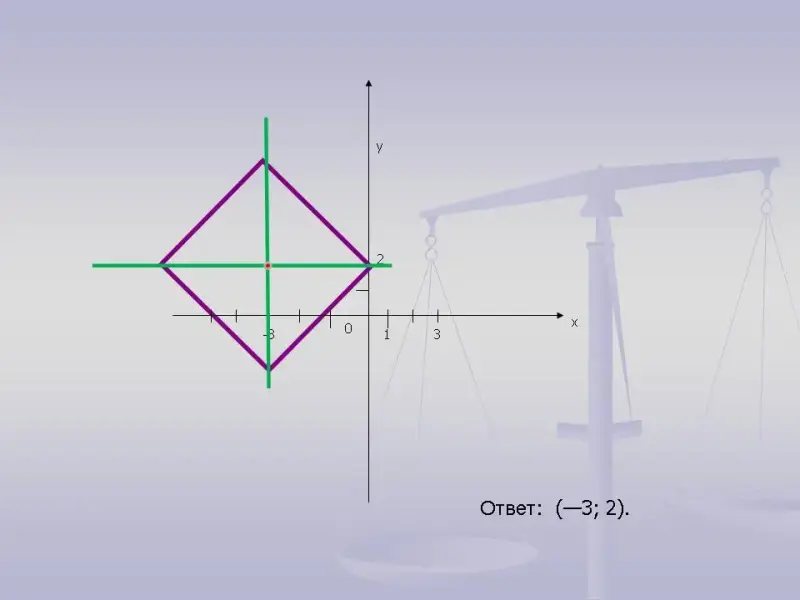
В результате мы получаем квадрат, центр которого (-3; 2), а длина диагонали равна 8, причем диагонали параллельны осям координат.
Из наглядных соображений можно сделать вывод: что уравнение вида | х + a | + | у + b | = с; задает на плоскости квадрат с центром в точке (- а; - b), диагоналями параллельными осям OX и ОУ, и длина каждой диагонали равна 2с. Ответ: (- 3; 2).
2. Решить уравнение aх = 1
Ответ: если a = 0, то нет решения; если a = 0, то х = 1/ a
3. Решить уравнение (а2 - 1) х = а + 1.
Решение.
Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи:
1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения
2) а = - 1; получаем ОX = О , и очевидно х - любое.
1
3) если а = + 1, то х = ---
а - 1
Ответ:
если а = - 1, то х - любое;
если а = 1, то нет решения;
1
если а = + 1 , то х = ---
а - 1
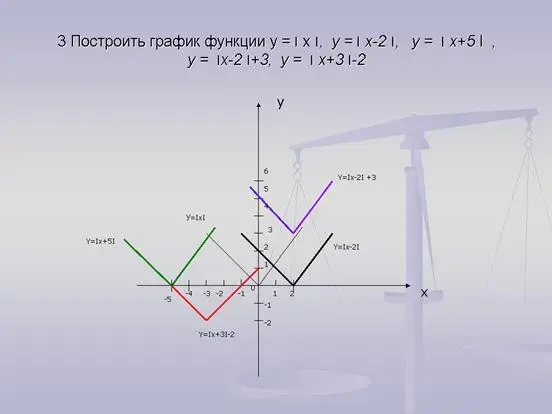
3. Решения примеров (из вариантов С)
1. При каком значении параметра р уравнение | х2 - 5х + 6 | + | х2 - 5х + 4 | = р имеет четыре корня.
Решение.
Рассмотрим функцию у = | х2 - 5х + 6 | + | х2 - 5х + 4 |
Так как х2 - 5х + 6 = (х - 2)(х - 3) и х2 - 5х + 4 = (х - 1)(х - 4), то y = | (х - 2)(х - 3) | + | (х - 1)(х - 4) |, корни квадратных трехчленов отметим на числовой прямой

1 2 3 4 х
Числовая прямая при этом разбивает на 5 промежутков
1.
| { | x < 1 | { | x < 1 |
| y = x2 - 5x + 6 + x2 - 5x + 4 | y = 2x2 - 10x + 10 |
2.
| { | 1 < x < 2 | { | 1 < x < 2 |
| y = x2 - 5x + 6 - x2 + 5x - 4 | y = 2 |
3.
| { | 2 < x < 3 | { | 2 < x <3 |
| y = - 2x2 + 10x - 10 | y = - x2 + 5x - 6 - x2 + 5x - 4 |
4.
| { | 3 < x < 4 | { | 3 < x < 4 |
| y = 2 | y = x2 - 5x + 6 - x2 + 5x - 4 |
5.
| { | x > 4 | { | x > 4 |
| y = 2x2 - 10x + 10 | y= x2 - 5x + 6 + x2 -5x + 4 |
Для случая 3) х0 = - b | 2a = 2, y0 = 25 : 2 + 25 - 10 = 2,5
Итак, (2,5; 2,5) - координаты вершины параболы y = - 2x2 + 10x - 10.
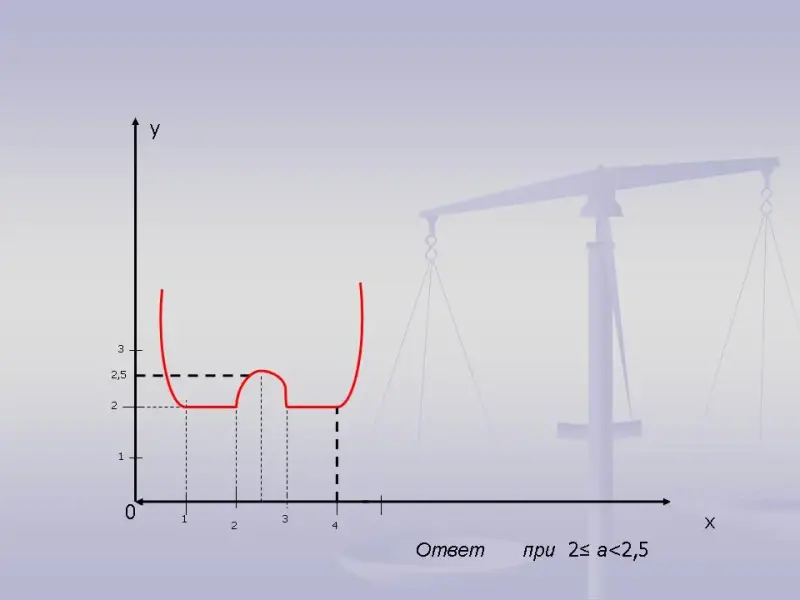
Построим график функции, заданной равенством

Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 < а < 2,5
Ответ: при 2 < а < 2,5
4. Самостоятельная работа по уровням
1 уровень
1. Решить уравнение х2 - | x | = 6
2. При каких целых значениях а имеет единственное решение уравнение ах2 - (а + 1) + а2 + а = 0?
2 уровень
1. Решить уравнение: | x - 5 | - | 2x + 3 | = 10
2. Найти все значениях параметра а, при которых уравнение (а -12) х2 + 2 = 2(12 - а) имеет два различных корня?
3 уровень
1. Решить уравнение | x - 5 | - | 2x + 3| = 10
2. Найти все значениях параметра а, при которых уравнение (а - 12) х2 + 2 = 2(12 - а) имеет два различных корня?
5. Итог урока
1. Определение модуля.
2. Что значит решить уравнение с параметром?
6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012