Семинар-практикум "Повторяя арифметическую и геометрическую прогрессии, повторяем алгебру"

Цель урока: Уметь применять знания по арифметической и геометрической прогрессиям при решении задач.

Задания представлены в двух вариантах и систематизированы по темам. Варианты могут быть использованы в самостоятельной работе, в работе по группам, в коллективной работе класса, в качестве индивидуальных заданий.

Системы уравнений

Вариант 1

1. В геометрической прогрессии сумма первого и второго членов равна 132, а сумма второго и третьего членов равна 110. Найдите три первые члена этой прогрессии.
2. Найдите четвертый член возрастающей арифметической прогрессии, в которой сумма первых десяти членов равна 155, а произведение ее первого и десятого членов равно 58.
3. В магазине в конце августа продали 1200 тетрадей трех видов по цене соответственно: 2 руб, 4 руб и 6 руб на сумму 4200 рублей. Сколько тетрадей каждого вида было продано в магазине , если количество проданных тетрадей соответственно каждого вида образуют арифметическую прогрессию?

Вариант 2

1. Найдите первые три члена геометрической прогрессии, если сумма первых ее трех членов равна 10,5 , а разность первого и четвертого членов равна 31,5.
2. Сумма первого и пятого членов возрастающей арифметической прогрессии равна 26, а произведение ее второго и четвертого членов равно 160. Найдите сумму первых шести членов прогрессии.
3. Цена поездки на электричке внутри города постоянна, а проезд в каждую пригородную зону увеличивает цену билета на одно и тоже число рублей. Рекламному агенту из города пришлось в понедельник ехать в первую зону, во вторник ехать во вторую зону, в среду в третью и т.д.. Каждый день он возвращался тоже на электричке. В понедельник и вторник он потратил на билеты 52 рубля, в среду и четверг – 84 рубля, а все его билеты стоили 322 рубля. Сколько дней подряд ездил агент.

Ответы и комментарии к заданиям.

Вариант 1

1. Решая составленную систему уравнений разделим почленно левую и правую части уравнений системы. При этом q = -1 не является решением системы, так как правые части обоих уравнений системы отличны от нуля. Ответ: b₁=72, b₂=60,b₃=50.

2. По теореме, обратной теореме Виета (если сумма двух чисел равна -p, а произведение равно q, то эти числа являются корнями уравнения +px+ q=0). Решением системы является пара корней квадратного уравнения -31x+58=0. Решениями будут числа 2 и 29. Так как арифметическая прогрессия возрастающая по условию, то , =29 Ответ : ₄=11.

3. Решить эту систему можно либо способом подстановки, либо способом сложения Ответ: 550,400,250 тетрадей.

Вариант 2

1. При решении системы уравнений применяется формула разности кубов. Ответ: b₁=3,5 , b₂= -7, b ₃=14.

2. Ответ: =87.

3. Пусть ₁ р. потратил рекламный агент в понедельник, во вторник – ₂ р., в среду – ₃ и т.д. , тогда Так как , то 2n²+9n-161=0 , n=7

Ответ: 7 дней.

Неравенства

Вариант 1

1. Найдите первый положительный член арифметической прогрессии: - 10,2 ; -9,5 ; … .
2. Найдите сумму всех двузначных чисел , которые при делении на 7 дают в остатке 1.
3. Укажите наибольшее число членов арифметической прогрессии : 3, 5, 7, … , сумма которых не превосходит 120.

Вариант 2

1. Найдите первый отрицательный член арифметической прогрессии : 15,6 ; 15 ; … .
2. Найдите сумму всех натуральных чисел , кратных 3, заключенных в промежутке от 100 до 200.
3. Укажите наибольшее число членов арифметической прогрессии: 17, 14, 11,… , при сложении которых получится положительное число.

Ответы и комментарии к заданиям.

Вариант 1

1. _n ; -10,2+0,7(n-1) ; n >15 , следовательно а₁₆ – первый положительный член арифметической прогрессии Ответ: ₁₆ =0,3.

2. _n = 7(n+1)+1 ; 7(n+1)+199 ; n13 ; S₁₃ = 741 Ответ : 741.

3. Ответ: 10.

Вариант 2

1. Ответ ₂₈ = -0,6.

2. 100< _n<200 ; 100<3n <200 ; 33 <n<66 ; 34n66 ; S_n=*33=4950 Ответ: 4950.

3. Ответ: 12.

Уравнения

Вариант 1

1. Является ли число -78 членом арифметической прогрессии ( _n) , в которой ₁=20 и ₇= - 22.
2. Решите уравнение 1+х+х²+х³+…+х⁹⁹=0.
3. Решите уравнение, в котором слагаемые в сумме, записанной в левой части уравнения, составляют арифметическую прогрессию: 1+7+13+…+х=280.

Вариант 2

1. В геометрической прогрессии (b_n) b₁=11 ; b_n=88 ; S_n=165 Найдите q и n.
2. Решите уравнение: 1+х+х²+х³+…+х¹⁰⁰=0.
3. Решите уравнение: (x+1)+(x+4)+( x+7)+…+(x+28)=155.

Ответы и комментарии к заданиям.

Вариант 1

1. ₇= ₁+6 d ; d= -7 ; -78=20-7(n-1) ; n =15 ; nN Ответ : да.

2. b₁=1 ; q=x ; S₁₀₀= ; S₁₀₀=0 ; x?1 ; x= -1 Ответ :-1.

3. S_n=280 ; *n =280 ; ₁=1; d=6 ; 3n ²-2n-280=0 , так как n>0 , то n =10 ; ₁₀=55 Ответ: 55.

Вариант 2

1. ; q=2 ; 2^{n -1}=8 ; n=4 Ответ : q=2 ; n=4.

2. b₁=1; q=x ; S₁₀₁= ;S₁₀₁=0 , так как x 1, то решений нет . Ответ: x.

3. 1+4+7+…+28+x_n=155 ; S_n+x_n =155 ; 28=1+3(n-1) ; n=10 ; S₁₀=145 ; 145+10x=155 ; x =1 Ответ: 1.

Среднее арифметическое и среднее геометрическое чисел

Вариант 1

1. В арифметической прогрессии ( _n) _{m+ n}=72 ; _m-n=8. Найдите _m.
2. В геометрической прогрессии (b_n) b₁₉*b₂₇=32 . Чему равно b₂₃?
3. Могут ли длины сторон прямоугольного треугольника составлять арифметическую прогрессию.

Вариант 2

1. В геометрической прогрессии (b_n) b_m+n=72 ; b_{m- n}=8. Найдите b_m.
2. В арифметической прогрессии ( _n) ₁₁+ ₂₅=39 . Чему равно ₁₈?
3. Числа , b,c являются последовательными членами арифметической прогрессии. Докажите, что числа ²+ b+b², ²+ c+c², b²+ bc+c² также являются последовательными членами некоторой арифметической прогрессии.

Ответы и комментарии к заданиям.

Вариант 1

1. _m= _{m+ n} - d* n ; _m= _{m -n} + d *n ; _m = ; _m = ; _m =40 . Каждый член арифметической прогрессии является средним арифметическим предыдущего и последующего членов, а также симметрично расположенных членов относительно данного . Ответ: 40.

2. b₂₃=± = ± = ±4 , так как b ₁₉ и b₂₇ расположенны симметрично относительно b₂₃ Ответ: ±4 .

3. Пусть _{1 2} - длины катетов, а₃ – длина гипотенузы, тогда +()² = ; 5+2 _{1 3}-3=0 ; ( ₁-₃) ( ₁+ ₃)=0 ; ( ₁-₃) ( ₁+ d)=0 ; ₁+d=0; ₁= - d. Так как ₁>0, то d <0, что не удовлетворяет условию задачи, следовательно, ₁ = _{3, 2}=(₃ + ₃)=_{3 ; 1} : ₂ : ₃ = : : 1. Ответ : да, если они относятся , как : : 1. Например треугольники со сторонами 3,4,5 ; 6,8,10; 9,12,15; ….

Вариант 2

1. Каждый член геометрической прогрессии является средним геометрическим предыдущего и последующего членов, а также симметрично расположенных членов относительно данного.

b_m= ; b_m= b_m-n *qⁿ ;| b_m|=, так как знаки членов последовательности могут чередоваться. b_m=± = ±24 . Ответ: ±24 .

2. ₁₈= =19,5, так как ₁₁ и ₂₅ расположенны симметрично относительно a₁₈ .Ответ:19,5.

3. По свойству арифметической прогрессии b = ; ²+ c+c² = ; ²+ c +c² = ; ²+ c+ c² = ( ²+c²+( +c )²) ; ²+ c+c ² = ²+ c+c² .

Изображение членов последовательности на координатной плоскости

Вариант 1

1. На рисунке (рисунок 1) изображены точками первые восемь членов арифметической прогрессии. Найдите ₂₁.
2. Изобразите на координатной плоскости первые пять членов арифметической прогрессии ( _n) и напишите уравнение прямой , на которой лежат построенные точки, если известно, что ₁₀= - 10 ; ₁₅ = - 17,5.
3. Известно, что b₇= ; b₁₀= - . Найдите первые шесть членов геометрической прогрессии ( b_n) и изобразите их на координатной плоскости. Определите характер монотонности функции, на графике которой лежат построенные точки.

Рисунок 1

Вариант 2

1. На рисунке (рисунок 2) изображены точками первые пять членов арифметической прогрессии. Найдите ₂₄.
2. Известно, что с₁₆=7 , с₂₃=11,2 . Изобразите на координатной плоскости первые шесть членов арифметической прогрессии (с_n) и напишите уравнение прямой на которой лежат построенные точки.
3. Найдите первые пять членов геометрической прогрессии (d_n) и изобразите их на координатной плоскости, если известно, что d₆= ; d₉ = . Определите характер монотонности функции, на графике которой лежат построенные точки.

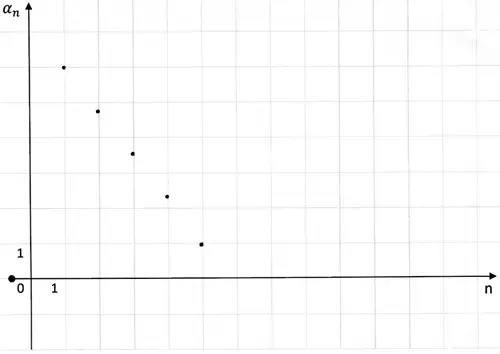
Рисунок 2

Ответы и комментарии к заданиям.

Вариант 1

1. Так как _n=k_n +l , где k =d , l = ₁ – d, то арифметическая прогрессия является линейной функцией y=k_n + l на множестве натуральных чисел , d=и равно , где - угол наклона прямой к оси абсцисс. Ответ : ₂₁ = 9.

2. ₁=3,5 ; d= - 1,5 ; ₂=2 ; ₃=0,5 ; ₄= - 1 ; ₅= -2,5 ; y =dx+( ₁-d ) ; y= - 1,5x +5 . Ответ: y= - 1,5 x+5.

3. q³= ; q= ; b ₁= - 4 ; b₂= - 2 ; b₃ = - 1 ; b₄ = - ; b₅ = - ; b₆ = - . Ответ: функция возрастает.

Вариант 2

1. d= - ; Ответ: ₂₄= - 22,75.

2. c₁ = - 2 ; d=0,6 ; c₂= -1,4 ; c₃ = -0,8 ; c₄ = - 0,2 ; c ₅= 0,4 ; c₆ =1 ; y=0,6x -2,6 . Ответ: y=0,6 x-2,6.

3. q³= ; q= ; d ₁=9 ; d₂=3 ; d₃=1 ; d ₄ = ; d₅= . Ответ: функция убывает.

Текстовые задачи

Вариант 1

1. Клиент взял в банке кредит на сумму 800000 рублей под 12 % годовых на 3 года. Какова прибыль банка?
2. При делении амебы , если она размножается без ограничений, получается две новые особи. Какое количество делений должно произойти для увеличения особей на 51100%?
3. Число радиоактивных атомов по истечении определенного периода времени (период полураспада) уменьшается в два раза. Сколько процентов атомов радиоактивного йода останется спустя три периода полураспада?

Вариант 2

1. Клиент открыл вклад на сумму 60000 рублей . Спустя два года он снял все проценты по вкладу, что в денежном эквиваленте составило 19350 рублей. Сколько процентов ежегодно начисляет банк по вкладу?
2. При делении гидры, если она размножается без ограничений , получаются пять новых особей. По истечении некоторого времени одна особь составляла 0,16% от всех особей. Сколько делений произошло за это время?
3. Число радиоактивных атомов по истечении определенного периода времени (период полураспада) уменьшается в два раза. Какая доля радиоактивных атомов некоторого элемента распадется за два периода полураспада?

Ответы и комментарии к заданиям.

Вариант 1

1. b₁=800000 ; q=1,12 ; b₄= b₁q ³ ;b₄=800000*(1,12)³=1123942,4 р, следовательно прибыль банка 1123942,4-800000=323942,4р. Ответ: 323942,4р .

2. Ответ: 9делений.

3. N₄=N ₁q³ ; q= ; N₄= ₁ . Ответ: 12,5%.

Вариант 2

1. b₁=60000 ; b₃=19350+60000=79350 ; b ₃=b₁ q² ; q ²= = 1,3225 ;q=1,15 . Значит процентная ставка по этому вкладу составляла 15% годовых . Ответ: 15%.

2. Ответ : 4 деления.

3. N₃=N ₁q² ; q= ; N₃=N ₁ ; N₁- N₃=N₁ ; Ответ : 0,75.

Подведение итогов урока.

Повторяя арифметическую и геометрическую прогрессии, мы повторили способы решения систем уравнений; решение линейных неравенств, неравенств второй степени, двойных неравенств; среднее арифметическое и среднее геометрическое чисел; функциональную зависимость.

Оценивается работа учащихся.

Литература:

1. Алгебра 9 класс, учебник, под редакцией С.А.Теляковского.
2. Алгебра и начала анализа, 9 и 11 выпускные классы, Е.В.Якушева и др..
3. Алгебра, 9 класс . Дополнительные главы к школьному учебнику, Ю.Н. Макарычев , Н.Г.Миндюк.
4. Алгебра 9 класс , ГИА, 2010 г. Типовые тестовые задания , ФИПИ. В.В. Мирошин.