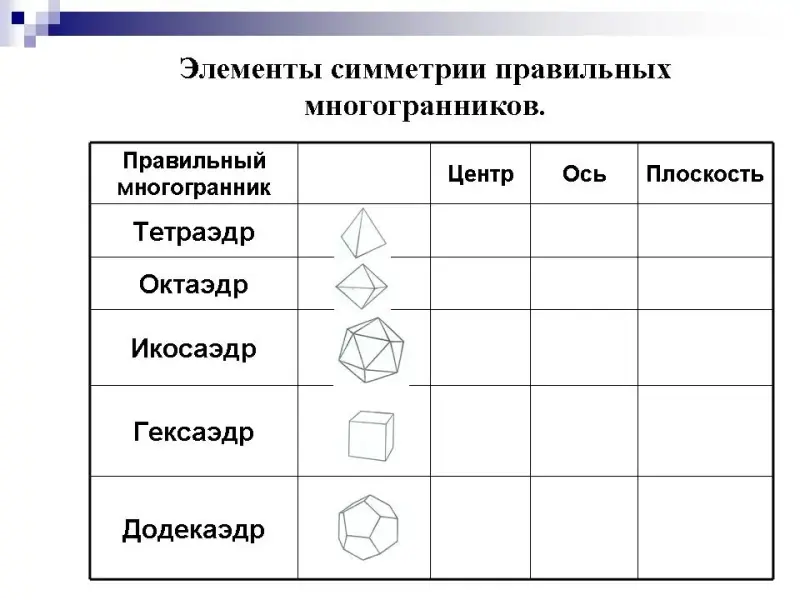
Урок по теме "Симметрия в пространстве"

Тип урока: комбинированный.

Цели урока:

• Рассмотреть осевую, центральную и зеркальную симметрии как свойства некоторых геометрических фигур.
• Научить строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.
• Совершенствовать навыки решения задач.

Задачи урока:

• Формирование пространственных представлений учащихся.
• Развитие умения наблюдать и рассуждать; развитие интереса к предмету через использование информационных технологий.
• Воспитание человека, умеющего ценить прекрасное.

Оборудование урока:

• Использование информационных технологий (презентация).
• Рисунки.
• Карточки с домашним заданием.

Ход урока 

I. Организационный момент.

Сообщить тему урока, сформулировать цели урока.

II. Введение.

Что такое симметрия?

Выдающийся математик Герман Вейль высоко оценил роль симметрии в современной науке: "Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство".

Мы живем в очень красивом и гармоничном мире. Нас окружают предметы, которые радуют глаз. Например, бабочка, кленовый лист, снежинка. Посмотрите, как они прекрасны. Вы обращали на них внимание? Сегодня мы с вами прикоснемся к этому прекрасному математическому явлению – симметрии. Познакомимся с понятием осевой, центральной и зеркальной симметрий. Будем учиться строить и определять симметричные относительно оси, центра и плоскости фигуры.

Слово “симметрия” в переводе с греческого звучит как “гармония”, означая красоту, соразмерность, пропорциональность, одинаковость в расположении частей. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.

В наиболее общем виде под "симметрией" в математике понимается такое преобразование пространства (плоскости), при котором каждая точка M переходит в другую точку M' относительно некоторой плоскости (или прямой) a, когда отрезок MM' является перпендикулярным плоскости (или прямой) a и делится ею пополам. Плоскость (прямая) a называется при этом плоскостью (или осью) симметрии. К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии. Плоскостью симметрии P называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение.

III. Основная часть. Виды симметрии.

Центральная симметрия

Симметрия относительно точки или центральная симметрия – это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.

Практическое задание.

1. Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
2. Какие из следующих букв имеют центр симметрии: А, О, М, Х, К?
3. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?

Осевая симметрия

Симметрия относительно прямой (или осевая симметрия) – это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.

Практическое задание.

1. Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
2. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О?
3. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
4. Сколько осей симметрии имеет рисунок? (см. рис. 1)

Рис. 1

Зеркальная симметрия

Точки А и В называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АВ и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной сама себе.

Практическое задание.

1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при: а) центральной симметрии относительно начала координат; б) осевой симметрии относительно координатных осей; в)зеркальной симметрии относительно координатных плоскостей.
2. В правую или левую перчатку переходит правая перчатка при зеркальной симметрии? осевой симметрии? центральной симметрии?
3. На рисунке показано, как цифра 4 отражается в двух зеркалах. Что будет видно на месте знака вопроса, если то же самое сделать с цифрой 5? (см. рис. 2)
4. На рисунке показано, как слово КЕНГУРУ отражается в двух зеркалах. Что получится, если то же самое проделать с числом 2011? (см. рис. 3)

Рис. 2

Рис. 3

Это интересно.

Симметрия в живой природе.

Почти все живые существа построены по законам симметрии, недаром в переводе с греческого слово «симметрия» означает «соразмерность».

Среди цветов, например, наблюдается поворотная симметрия. Многие цветы можно повернуть так, что каждый лепесток займет положение соседнего, цветок совместится с самим собой. Минимальный угол такого поворота для различных цветов неодинаков. Для ириса он равен 120°, для колокольчика – 72°, для нарцисса – 60°.

В расположении листьев на стеблях растений наблюдается винтовая симметрия. Располагаясь винтом по стеблю, листья как бы раскидываются в разные стороны и не заслоняют друг друга от света, хотя сами листья тоже имеют ось симметрии. Рассматривая общий план строения какого-либо животного, мы замечаем обычно известную правильность в расположении частей тела или органов, которые повторяются вокруг некоторой оси или занимают одно и то же положение по отношению к некоторой плоскости. Эту правильность называют симметрией тела. Явления симметрии столь широко распространены в животном мире, что весьма трудно указать группу, в которой никакой симметрии тела подметить нельзя. Симметрией обладают и маленькие насекомые, и крупные животные.

Симметрия в неживой природе.

Среди бесконечного разнообразия форм неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. Наблюдая за красотой природы, можно заметить, что при отражении предметов в лужах, озерах проявляется зеркальная симметрия (см. рис. 4).

В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают поворотной симметрией и, кроме того, зеркальной симметрией.

Нельзя не увидеть симметрию и в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Так как гранат имеет те же элементы что и куб, он высоко ценится знатоками драгоценных камней. Художественные изделия из гранатов были обнаружены в могилах Древнего Египта, относящихся еще к додинастическому периоду (свыше двух тысячелетий до н.э.) (см. рис. 5).

В коллекциях Эрмитажа особым вниманием пользуются золотые украшения древних скифов. Необычайно тонка художественная работа золотых венков, диадем, дерева и украшенных драгоценными красно-фиолетовыми гранатами.

Одним из самых наглядных использований законов симметрии в жизни служат строения архитектуры. Это то, что чаще всего мы можем увидеть. В архитектуре оси симметрии используются как средства выражения архитектурного замысла (см. рис. 6). В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях.

Еще одним примером использования человеком симметрии в своей практике – это техника. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Или одно из важнейших изобретений человечества, имеющих центр симметрии, является колесо, также центр симметрии есть у пропеллера и других технических средств.

«Посмотри в зеркало!»

Должны ли мы считать, что самих себя видим только в «зеркальном отражении»? Или в лучшем случае лишь на фото и кинопленке можем узнать, как мы выглядим «на самом деле»? Конечно, нет: достаточно зеркальное изображение вторично отразить в зеркале, чтобы увидеть свое истинное лицо. На помощь приходят трельяжи. Они имеют одно большое главное зеркало в центре и два меньших зеркала по сторонам. Если такое боковое зеркало поставить под прямым углом к среднему, то можно увидеть себя именно в том виде, в каком вас видят окружающие. Зажмурьте левый глаз, и ваше отражение во втором зеркале повторит ваше движение левым глазом. Перед трельяжем вы можете выбирать, хотите ли вы увидеть себя в зеркальном или в непосредственном изображении.

Легко вообразить, какая бы царила на Земле неразбериха, если бы симметрия в природе была нарушена! 

Рис. 4	Рис. 5	Рис. 6

IV. Физкультминутка.

• «Ленивые восьмерки» – активизируют структуры, обеспечивающие запоминание, повышают устойчивость внимания.
  Нарисовать в воздухе в горизонтальной плоскости цифру восемь по три раза сначала одной рукой, затем сразу обеими руками.
• «Симметричные рисунки» – улучшают зрительно-моторную координацию, облегчают процесс письма.
  Нарисовать в воздухе обеими руками симметричные рисунки. 

V. Самостоятельная работа проверочного характера.

Ι вариант

1. В прямоугольнике АВСD О – точка пересечения диагоналей, BH и DE – высоты треугольников АВО и COD соответственно, BOH = 60°, AH = 5 см. Найдите ОЕ.
2. В ромбе АВСD диагонали пересекаются в точке О. ОМ, ОК, ОЕ – перпендикуляры, опущенные на стороны АВ, ВС, CD соответственно. Докажите, что ОМ = ОК, и найдите сумму углов МОВ и СОЕ.
3. Внутри данного острого угла постройте квадрат с данной стороной так, чтобы две вершины квадрата принадлежали одной стороне угла, а третья – другой.

ΙΙ вариант

1. В прямоугольнике MPKH О – точка пересечения диагоналей, РА и BH – перпендикуляры, проведенные из вершин Р и H к прямой МК. Известно, что МА = ОВ. Найдите угол РОМ.
2. В ромбе MPKH диагонали пересекаются в точке О. На сторонах МК, KH, PH взяты точки А, В, С соответственно, АК = КВ = РС. Докажите, что ОА = ОВ, и найдите сумму углов РОС и МОА.
3. Постройте квадрат по данной диагонали так, чтобы две противоположные вершины этого квадрата лежали на разных сторонах данного острого угла.

VI. Подведение итогов урока. Оценивание.

Вопросы:

• С какими видами симметрии вы познакомились на уроке?
• Какие две точки называются симметричными относительно данной прямой?
• Какая фигура называется симметричной относительно данной прямой?
• Какие две точки называются симметричными относительно данной точки?
• Какая фигура называется симметричной относительно данной точки?
• Что такое зеркальная симметрия?
• Приведите примеры фигур, обладающих: а) осевой симметрией; б) центральной симметрией; в) и осевой, и центральной симметрией.
• Приведите примеры симметрии в живой и неживой природе.

VII. Домашнее задание.

1. Индивидуальное: достройте, применив осевую симметрию (см. рис. 7).

Рис. 7

2. Постройте фигуру, симметричную данной относительно: а) точки; б) прямой (см. рис. 8, 9).

Рис. 8	Рис. 9

3. Творческое задание: «В мире животных». Нарисуйте представителя из мира животных и покажите ось симметрии.

VIII. Рефлексия.

• Что понравилось на уроке?
• Какой материал был наиболее интересен?
• Какие трудности возникли при выполнении того или иного задания?
• Что бы вы изменили в ходе урока?