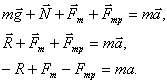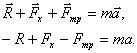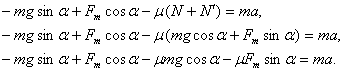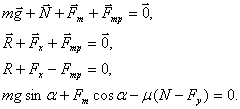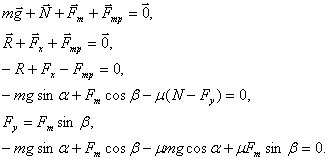Итак, постараюсь подробно описать ход моих
рассуждений по этому вопросу. На первом уроке
ставлю перед учащимися вопрос: как может тело
двигаться по наклонной плоскости? Вместе
отвечаем: скатываться равномерно, с ускорением;
покоиться на наклонной плоскости; удерживаться
на ней; съезжать под действием силы тяги
равномерно, с ускорением; заезжать под действием
силы тяги равномерно, с ускорением. На рисунках
на двух-трех примерах показываем, какие при этом
на тело действуют силы. Попутно ввожу понятие
скатывающей равнодействующей. Записываем
уравнение движения в векторной форме, затем в нем
заменяем сумму 
скатывающей
равнодействующей 
(обозначайте,
как вам нравится). Это делаем по двум причинам:
во-первых, нет необходимости проецировать
векторы сил на ось 
и решать два уравнения; во-вторых,
правильно будет показано соотношение сил, исходя
из условия задачи.
Покажу на конкретных примерах. Пример 1: тело под действием силы тяги съезжает равномерно (Рисунок 1).
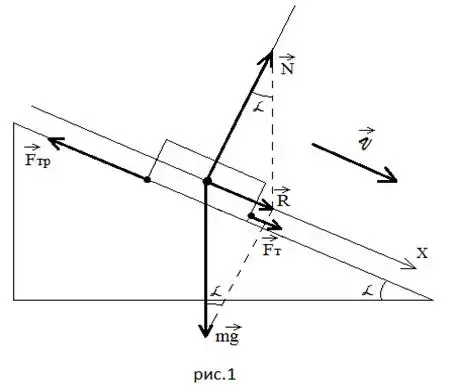
Ученики первым делом должны усвоить алгоритм
построения рисунка. Изображаем наклонную
плоскость, посередине нее – тело в виде
прямоугольника, через середину тела параллельно
наклонной плоскости проводим ось 
. Направление оси не
существенно, но в случае равноускоренного
движения лучше показать в сторону вектора 
, чтобы в
алгебраической форме в уравнении движения в
правой части перед 
был знак «плюс». Далее строим силы.
Силу тяжести 
проводим
вертикально вниз произвольной длины (требую
рисунки делать крупными, чтобы всем было все
понятно). Затем из точки приложения силы тяжести
– перпендикуляр к оси , вдоль которого пойдет сила реакции
опоры 
.
Параллельно этому перпендикуляру из конца
вектора проводим
пунктирную линию до пересечения с осью . Из этой точки –
пунктирную линию, параллельную до пересечения с
перпендикуляром – получаем вектор правильной длины.
Таким образом, мы построили параллелограмм на
векторах и , автоматически
указав правильную величину силы реакции опоры и
построив по всем правилам векторной геометрии
равнодействующую этих сил , которую я называю скатывающей
равнодействующей (диагональ, совпадающая с осью ). В этом месте,
воспользовавшись методом из учебника, на
отдельном рисунке показываю силу реакции опоры
произвольной длины: сначала короче, чем нужно, а
потом длиннее, чем нужно. Показываю
равнодействующую силы тяжести и силы реакции
опоры: в первом случае она направлена вниз под
углом к наклонной плоскости (Рисунок 2), во втором
случае – вверх под углом к наклонной плоскости
(Рисунок 3).
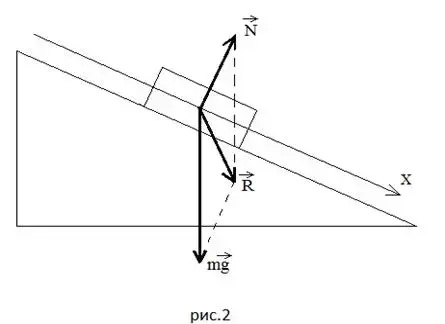
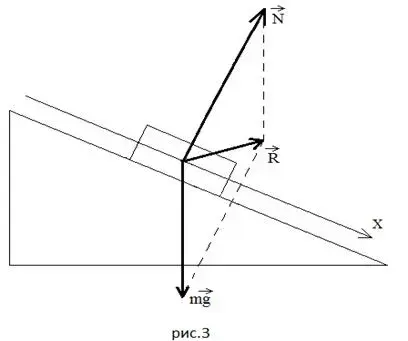
Делаем очень важный вывод: соотношение между
силой тяжести и силой реакции опоры должно быть
таким, чтобы тело под их действием (или под
действием скатывающей равнодействующей) в
отсутствие других сил двигалось вниз вдоль
наклонной плоскости. Далее я спрашиваю:
какие еще силы действуют на тело? Ребята
отвечают: сила тяги и сила трения. Я задаю
следующий вопрос: какую силу покажем сначала, а
какую потом? Добиваюсь правильного и
обоснованного ответа: сначала в этом случае надо
показать силу тяги, а затем силу трения, модуль
которой будет равен сумме модулей силы тяги и
скатывающей равнодействующей: 
, т.к. по условию задачи тело
движется равномерно, следовательно,
равнодействующая всех сил, действующих на тело,
должна равняться нулю согласно первому закону
Ньютона. Для контроля задаю провокационный
вопрос: так сколько сил действует на тело? Ребята
должны ответить – четыре (не пять!): сила тяжести,
сила реакции опоры, сила тяги и сила трения.
Теперь записываем уравнение движения в
векторной форме согласно первому закону Ньютона:
.
Заменяем сумму векторов скатывающей равнодействующей :
.
Получаем уравнение, в котором все векторы
параллельны оси .
Теперь запишем это уравнение через проекции
векторов на ось :
.
Эту запись в дальнейшем можно пропускать. Заменим в уравнении проекции векторов на их модули с учетом направлений:
.
Пример 2: тело под действием силы тяги заезжает на наклонную плоскость с ускорением (Рисунок 4).
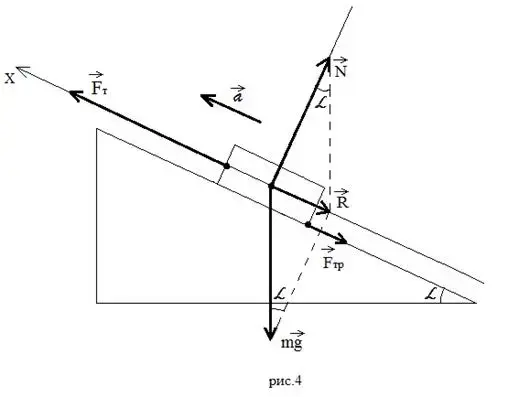
В этом примере ученики должны сказать, что
после построения силы тяжести, силы реакции
опоры и скатывающей равнодействующей следующей
надо показать силу трения, последним – вектор
силы тяги, который должен быть больше суммы
векторов 
, т.к.
равнодействующая всех сил должна быть
направлена так же, как вектор ускорения согласно второму
закону Ньютона. Уравнение движения тела должны
записать согласно второму закону Ньютона:
Если есть возможность на уроке рассмотреть
другие случаи, то не пренебрегаем этой
возможностью. Если нет, то даю это задание домой.
Кто-то может рассмотреть все оставшиеся случаи,
кто-то некоторые – право выбора учеников. На
следующем уроке проверяем, исправляем ошибки и
переходим к решению конкретных задач,
предварительно выразив из векторных
треугольников и
:
,
.
Равенство (2) желательно проанализировать для
различных углов 
.
При 
имеем: 
, как при движении
горизонтально под действием горизонтальной силы
тяги. С ростом угла его косинус уменьшается,
следовательно, уменьшается и сила реакции опоры
и становится все меньше и меньше силы тяжести.
При угле 
она
равна нулю, т.е. тело не действует на опору и
опора, соответственно, «не реагирует».
Предвижу вопрос оппонентов: как применить эту методику для случаев, когда сила тяги горизонтальна или направлена под углом к наклонной плоскости? Отвечу на конкретных примерах.
а) Тело с ускорением затаскивают на наклонную плоскость, прикладывая силу тяги горизонтально (Рисунок 5).
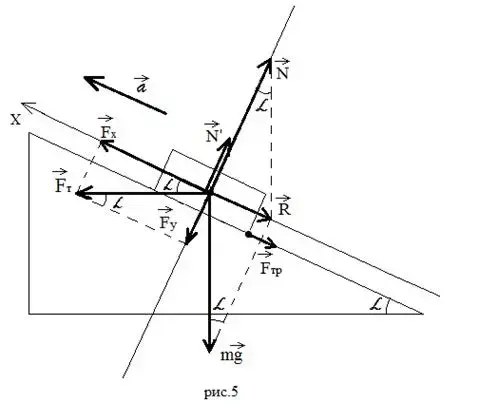
Горизонтальную силу тяги 
раскладываем на две
составляющие: вдоль оси – 
и
перпендикулярную оси – 
(операция,
обратная построению равнодействующей
перпендикулярных сил). Записываем уравнение
движения:
.
Заменяем скатывающей
равнодействующей, а вместо пишем :
Из векторных треугольников выражаем 
: 
и 
: 
.
Под действием горизонтальной силы тело не только
поднимается вверх по наклонной плоскости, но еще
и дополнительно прижимается к ней. Поэтому
возникает дополнительная сила давления, равная
модулю вектора и,
согласно третьему закону Ньютона,
дополнительная сила реакции опоры 
: 
. Тогда сила трения будет: 
.
Уравнение движения примет вид:
Вот мы полностью расшифровали уравнение движения. Теперь осталось выразить из него искомую величину. Попробуйте решить эту задачу традиционным способом и вы получите такое же уравнение, только решение будет громоздче.
б) Тело стаскивают равномерно с наклонной плоскости, прикладывая силу тяги горизонтально (Рисунок 6).
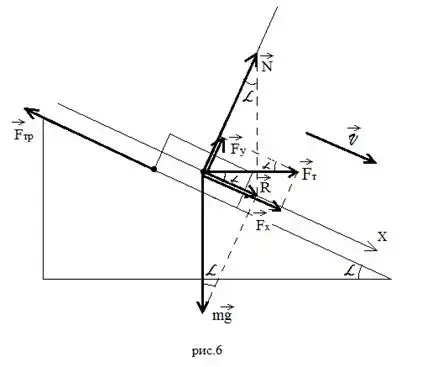
В этом случае сила тяги кроме стаскивания тела вниз вдоль наклонной плоскости еще и отрывает его от наклонной плоскости. Итак, окончательное уравнение имеет вид:
.
в) Тело затаскивают равномерно на наклонную
плоскость, прикладывая силу тяги под углом 
к наклонной
плоскости (Рисунок 7).
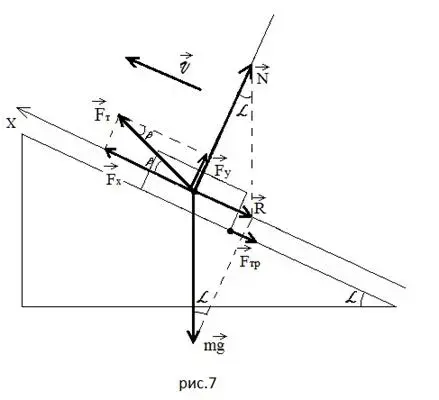
Предлагаю рассмотреть конкретные задачи, дабы еще убедительнее прорекламировать мой методический подход к решению таких задач. Но прежде обращаю внимание на алгоритм решения (я думаю, все учителя физики на него обращают внимание учеников, и все мое повествование было подчинено этому алгоритму):
1) внимательно прочитав задачу, выяснить, как
движется тело;
2) сделать рисунок с правильным, исходя из условия
задачи, изображением сил;
3) записать уравнение движения в векторной форме
согласно первому или второму закону Ньютона;
4) записать это уравнение через проекции векторов
сил на ось x (этот шаг в дальнейшем, когда умение
решать задачи по динамике будет доведено до
автоматизма, можно опустить);
5) выразить проекции векторов через их модули с
учетом направлений и записать уравнение в
алгебраической форме;
6) выразить модули сил по формулам (если есть
необходимость);
7) выразить искомую величину.
Задача 1. За какое время 
тело массой 
соскальзывает с наклонной
плоскости высотой 
и углом наклона , если по наклонной плоскости с
углом наклона оно
движется равномерно?
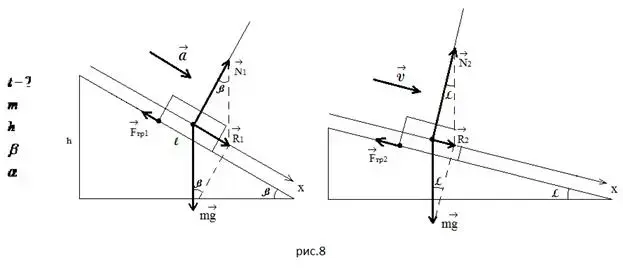
Каково было бы решать эту задачу привычным способом!
Задача 2. Что легче: удержать тело на наклонной плоскости или двигать его по ней равномерно вверх?
Здесь при объяснении без скатывающей равнодействующей, на мой взгляд, не обойтись.
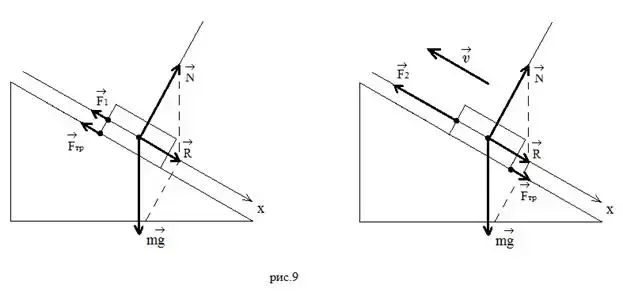
Как видно из рисунков, в первом случае сила
трения помогает удерживать тело (направлена в ту
же сторону, что и удерживающая сила), во втором
случае она вместе со скатывающей
равнодействующей направлена против движения. В
первом случае 
,
во втором случае 
.