Метод масс в геометрии
Учитель: Сегодня на уроке мы рассмотрим один интересный метод решения ряда геометрических задач. Называется этот метод "Метод масс". (слайд №1)
Родоначальником метода масс был великий древнегреческий мыслитель Архимед. Еще в 3 веке до нашей эры он обнаружил возможность доказывать новые математические факты с помощью свойств центра масс (барицентра). В частности, этим способом была установлена теорема о том, что три медианы треугольника пересекаются в одной точке.
Несколько простых свойств центра масс позволяют решать различные задачи геометрии и алгебры.
Доклад учащегося об Архимеде. Приложение 1.
(слайды №№ 2-6)
Учитель: Из курса физики известно, что материальной точкой можно назвать тело, размерами которого можно пренебречь, то есть, фактически, материальная точка - точка, снабженная массой. Выражение "mА" означает: точка А массой m.
Множество материальных точек - система материальных точек (СМТ).
(Слайд №7)
Учитель: Давайте представим, что мы подвесили карандаш на ниточке. (Слайд №8).
В зависимости от того, в каком месте карандаша будет располагаться наша ниточка, карандаш будет висеть либо параллельно полу - либо нет. Если мы смогли найти такое положение нитки, что карандаш висит параллельно полу - это значит, что ниточка обхватывает наш карандаш в центре масс.
Давайте вспомним детские качели. (Слайд №9). Подскажите псу куда нужно ему пересесть, что74бы качели пришли в равновесие?
Правильно. (Слайд №10)
А сейчас я хочу познакомить вас с постулатами Архимеда.
(Слайды 11-12)
Любая конечная система материальных точек имеет единственный центр масс.
2. Система, состоящая из двух материальных точек имеет центр масс, принадлежащий отрезку, соединяющему эти точки причем его положение определяется правилом рычага: m1d1=m2d2
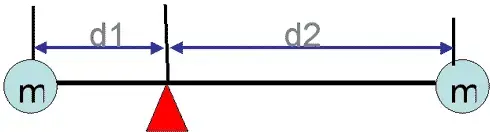
3. Если в системе, состоящей из конечного числа материальных точек, отметить несколько материальных точек и массы всех отмеченных точек перенести в их центр масс, то от этого положение центра масс всей системы не изменится.
(слайд №13)
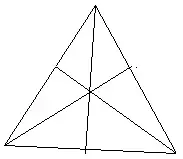
Задача Архимеда (о медианах треугольника): медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины.
Дано:
Треугольник АВС- произвольный
АА1, ВВ1, СС1 - медианы
Доказать: АО:ОA1 = 2:1, ВО:ОВ1 = 2:1,
СО:ОС1 = 2:1.
Доказательство:
Пусть точка пересечения медиан - центр масс треугольника.
(слайд №13)
Помещаем в вершину А массу, равную единице. Поскольку точка В1 делит сторону АС пополам, то и в точку С должна быть помещена масса, равная единице. Аналогично и в точку В , т. к. А1 - тоже середина.
Имеем
1. СМТ 1А, 1В, 1С с центром масс в т. О.
2. 1А+1С=2В1. Рассмотрим СМT 1В, 2В1 с центром масс в т.О. Тогда по правилу рычага имеем ВО:ОВ1 = 2:1.
3. 1В+1С=2А1. Рассмотрим СМT 1А, 2А1 с центром масс в т.О. Тогда по правилу рычага имеем АО:ОА1 = 2:1.
4. Аналогично СО:ОС1 = 2:1. Что и требовалось доказать.
Задача №1.
В треугольнике АВС проведены чевианы ВМ и АN так, что ВN: NC=1:5, а АМ: МС=1:2. Найти ВО:ОМ и АО:ON, гдеО - точка пересечения чевиан.
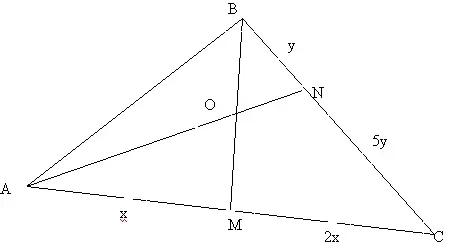
(Слайд №15)
Решение. (Слайд №16)
Помещаем в вершину С массу, равную единице. Поскольку точка М делит сторону АС в отношении 1:2, то по правилу рычага в точку А должна быть помещена масса, равная двум. Аналогично в точку В быть помещена масса, равная пяти, т. к. ВN: NC=1:5
1)СМТ 2А,5В,1С с центром масс в точке О.
2) 2A+1C=3M; 5В,3М - сист. Мат точек с ц.м. в т.О
По правилу рычага ВО:ОМ=3:5
3) 5В+1C=6N; 6N, 2А - сист. Мат точек с ц.м. в т.О
По правилу рычага АО:ОN=6:2=3:1
Ответ: ВО:ОМ=3:5, АО:ОN=6:2=3:1
Задача №2.
В треугольнике АВС проведены чевианы ВМ и АN так, что ВN: NC=1:7, а АМ: МС=2:5. Найти какую часть площади АВС составляет площадь СМОN.
(Слайд №17)
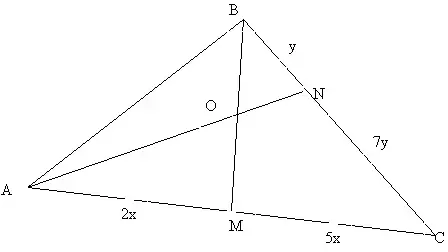
Решение.(Слайд 18)
Помещаем в вершину С массу, равную двум. Тогда по правилу рычага в точку А должна быть помещена масса, равная пяти,так как АМ: МС=2:5. Аналогично в точку В быть помещена масса, равная 14, т. к. ВN: NC=1:7, а в тоске С масса 2.
1)Введем систему материальных точек 5А,14В,2С с центром масс в точке О.
2) 5A+2C=7M; 14В,7М - СМТ с ц.м. в т.О . По правилу рычага ВО:ОМ=7:14=1:2
![]()
3) 14В+2C=16N; 16N, 5А - СМТ с ЦМ. в т.О. По правилу рычага АО:ОN=16:5=3:1
4) SCMON= ![]()
Итоги урока: Сегодня на уроке мы познакомились с инересным методом решения геометрических задач - методом масс. А так же узнали интересные факты их жизни создателя этого метода - Архимеда.
Домашнее задание: (слайд 23)
1. В треугольнике АВС проведены чевианы ВМ и АN так, что ВN: NC=2:3, а АМ: МС=2:1. Найти ВО:ОМ и АО:ON, гдеО - точка пересечения чевиан.
2. В треугольнике АВС проведены чевианы ВМ и АN так, что ВN: NC=4:3, а АМ: МС=2:3. Найти какую часть площади АВС составляет площадь СМОN.
3. В треугольнике АВС на стороне ВС выбрана точка D так, что BD : DC=1:2. Медиана СЕ пересекает отрезок АВ в точке F. Какую часть площади треугольника АВС составляет площадь треугольника АЕF?
Использованная литература:
- Балк М.Б., Болтянский В.Г. Геометрия масс
- Мякишев А.Г. Элементы геометрии треугольника
- Никулин А.В., Кукуш А.Г., Татаренко Ю.С. Геометрия на плоскости