1. Графическое решение уравнений
«Решить графически уравнение
».
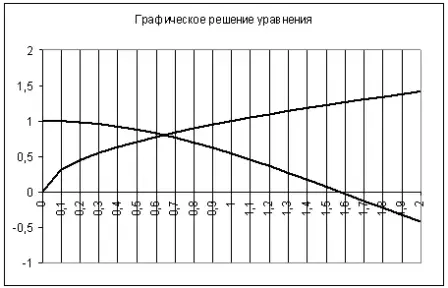
Для графического решения построим графики каждой из функций на отрезке [0, 2] с шагом (изменением х) 0.1. Чтобы построить графики функций для каждой функции построим таблицу значений, используя стандартные функции COS и КОРЕНЬ.
| x | cos(x) | корень(х) |
| 0 | 1 | 0 |
| 0,1 | 0,995 | 0,316228 |
| 0,2 | 0,9801 | 0,447214 |
| 0,3 | 0,9553 | 0,547723 |
| 0,4 | 0,9211 | 0,632456 |
| 0,5 | 0,8776 | 0,707107 |
| 0,6 | 0,8253 | 0,774597 |
| 0,7 | 0,7648 | 0,83666 |
| 0,8 | 0,6967 | 0,894427 |
| 0,9 | 0,6216 | 0,948683 |
| 1 | 0,5403 | 1 |
| 1,1 | 0,4536 | 1,048809 |
| 1,2 | 0,3624 | 1,095445 |
| 1,3 | 0,2675 | 1,140175 |
| 1,4 | 0,17 | 1,183216 |
| 1,5 | 0,0707 | 1,224745 |
| 1,6 | -0,029 | 1,264911 |
| 1,7 | -0,129 | 1,30384 |
| 1,8 | -0,227 | 1,341641 |
| 1,9 | -0,323 | 1,378405 |
| 2 | -0,416 | 1,414214 |
Примечание к построению диаграммы:
а) Для построения диаграммы выделяем столбцы cos(x) и корень(х).
б) При построении диаграммы на 2-ом шаге (Источник данных) нужно задать масштаб оси Х:
- перейти на вкладку «Ряд»,
- установить курсор в окно «Подписи оси Х»
- выделить в таблице все ячейки столбца «х» от 0 до 2
- нажать «Далее».
в) после построения графиков необходимо отредактировать точку пересечения осей
В результате построения графиков функций видно, что корень уравнения
приблизительно равен 0.64.
2. Табличное решения уравнений с заданной степенью точности
| x |  |
| 0 | 1 |
| 0,1 | 0,678776399 |
| 0,2 | 0,532852982 |
| 0,3 | 0,407613932 |
| 0,4 | 0,288605462 |
| 0,5 | 0,170475781 |
| 0,6 | 0,050738946 |
| 0,7 | -0,071817839 |
| 0,8 | -0,197720482 |
| 0,9 | -0,32707333 |
| 1 | -0,459697694 |
«Решить уравнение 
с точностью
».
Модуль показателя степени точности указывает сколько точных цифр должно быть в ответе. В нашем пример ответ должен быть получен с точностью 6 цифр после десятичной запятой (точки).
2.1. Построим схематические графики функций 
(см. п.1).
Очевидно, что корень уравнения находится внутри отрезка [0, 1].
2.2. создаем следующую таблицу Excel:
- в столбец А с помощью автозаполнения вводим все значения х из отрезка [0, 1] с шагом 0.1
- в столбец B вводим формулу =COS(X) – КОРЕНЬ(Х), где в качестве Х выступают ссылки на соответствующую ячейку столбца А
- скопируем формулу на соседние ячейки столбца B, используя автозаполнение.
| x |  |
x |  |
| 0 | 1 | 0,6 | 0,050738946 |
| 0,1 | 0,678776399 | 0,61 | 0,03862305 |
| 0,2 | 0,532852982 | 0,62 | 0,026477669 |
| 0,3 | 0,407613932 | 0,63 | 0,014302115 |
| 0,4 | 0,288605462 | 0,64 | 0,002095758 |
| 0,5 | 0,170475781 | 0,65 | -0,010141976 |
| 0,6 | 0,050738946 | 0,66 | -0,022411609 |
| 0,7 | -0,071817839 | 0,67 | -0,034713611 |
| 0,8 | -0,197720482 | 0,68 | -0,047048406 |
| 0,9 | -0,32707333 | 0,69 | -0,059416371 |
| 1 | -0,459697694 | 0,7 | -0,071817839 |
- в столбце B находим два соседних значения разного знака – соответствубщие им значения из столбца А определяют новый (более точный) отрезок нахождения корня [0.6, 0.7].
2.3. Повторяем действия п.п. а) – г) для столбцов C и D, отрезка [0.6, 0.7] и шага, уменьшеннего в 10 раз =0.01. В результате получаем новую таблицу, в которой выделяем соседние значения столбца D разного знака и получаем новый отрезок [0.64, 0.65] и новый шаг =0.001
2.4. Таким образом на каждом этапе находим соседние значения 
разного знака, соответствующие значения х образуют новый, более точный отрезок нахождения корня, шаг на каждом этапе уменьшается в 10 раз. Так как числа в ячейках получаются с большим количеством цифр – необходимо задать соответствующий формат представления данных. В результате получаем 6 таблиц:
| 1 таблица | 2 таблица | 3 таблица | |||
| x |  |
x |  |
x |  |
| 0 | 1 | 0,6 | 0,050738946 | 0,64 | 0,002095758 |
| 0,1 | 0,678776399 | 0,61 | 0,03862305 | 0,641 | 0,000873405 |
| 0,2 | 0,532852982 | 0,62 | 0,026477669 | 0,642 | -0,000349261 |
| 0,3 | 0,407613932 | 0,63 | 0,014302115 | 0,643 | -0,001572243 |
| 0,4 | 0,288605462 | 0,64 | 0,002095758 | 0,644 | -0,00279554 |
| 0,5 | 0,170475781 | 0,65 | -0,010141976 | 0,645 | -0,004019153 |
| 0,6 | 0,050738946 | 0,66 | -0,022411609 | 0,646 | -0,005243083 |
| 0,7 | -0,071817839 | 0,67 | -0,034713611 | 0,647 | -0,006467329 |
| 0,8 | -0,197720482 | 0,68 | -0,047048406 | 0,648 | -0,007691894 |
| 0,9 | -0,32707333 | 0,69 | -0,059416371 | 0,649 | -0,008916776 |
| 1 | -0,459697694 | 0,7 | -0,071817839 | 0,65 | -0,010141976 |
| 4 таблица | 5 таблица | 6 таблица | |||
| x |  |
x |  |
x |  |
| 0,641 | 0,000873405 | 0,6417 | 0,000017572 | 0,64171 | 0,000005344 |
| 0,6411 | 0,000751153 | 0,64171 | 0,000005344 | 0,641711 | 0,000004122 |
| 0,6412 | 0,000628897 | 0,64172 | -0,000006883 | 0,641712 | 0,000002899 |
| 0,6413 | 0,000506638 | 0,64173 | -0,000019110 | 0,641713 | 0,000001676 |
| 0,6414 | 0,000384376 | 0,64174 | -0,000031338 | 0,641714 | 0,000000453 |
| 0,6415 | 0,000262111 | 0,64175 | -0,000043565 | 0,641715 | -0,000000769 |
| 0,6416 | 0,000139843 | 0,64176 | -0,000055793 | 0,641716 | -0,000001992 |
| 0,6417 | 0,000017572 | 0,64177 | -0,000068020 | 0,641717 | -0,000003215 |
| 0,6418 | -0,000104703 | 0,64178 | -0,000080248 | 0,641718 | -0,000004437 |
| 0,6419 | -0,000226981 | 0,64179 | -0,000092475 | 0,641719 | -0,000005660 |
| 0,642 | -0,000349261 | 0,6418 | -0,000104703 | 0,64172 | -0,000006883 |
Завершаем построения таблиц, когда в столбце с Х получим числа с 6 цифрами после десятичной запятой (точки). Для определения корня в последнем заполненном столбце находим наименьшее по модулю значение. Соответствующее ему значение в столбце Х и будет корнем.
Таким образом, корень уравнения Х=0,641714
3. Решение текстовых задач с использованием формул
Решим задачу «Дана сторона квадрата. Вычислить его площадь и периметр».
Решение задачи.
а) Составим математическую модель задачи – перечислим формулы, используемые для ее решения: S = a; P = 4×a.
б) Подготовим таблицу решения:
- в ячейку А1 введем название задачи, отцентрируем по группе ячеек А1:Е1
- в ячейку А3 введем текст ввода, отцентрируем по группе ячеек А3:С3
- в ячейку А4 введем текст площади, отцентрируем по группе ячеек А4:С4
- в ячейку А5 введем текст периметра, отцентрируем по группе ячеек А5:С5
- в ячейку D4 введем формулу площади =D3*D3
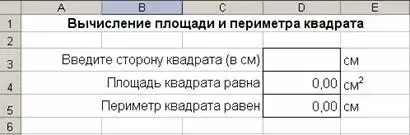
- в ячейку D5 введем формулу периметра =4*D3
- установим для группы ячеек D3:D5 числовой формат с двумя десятичными знаками;
- отформатируем шрифт, выравнивание и обрамление ячеек.
в) Введем исходные данные и получим результаты.
В ячейку D3 введем значение стороны квадрата, в ячейках D4 и D5 получим соответственно значения площади и периметра. Результаты запишем в тетрадь.
Кроме ссылок на ячейки при решении текстовых задач могут быть использованы стандартные функции.
4. Исследование различных процессов с помощью электронных таблиц
Рассмотрим физический процесс: «Тело брошено вертикально вверх с начальной скоростью V0 с высоты H0». Исследуем изменение его местоположения и скорости в зависимости от времени.
а) Построим математическую модель задачи:
- скорость тела изменяется по закону
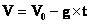
- высота тела изменяется по закону H = H0 + V0×t – g×t2/2.
б) Исследование процесса состоит в построении компьютерной модели – таблиц и графиков зависимости скорости и высоты от времени. Выполним построение таблиц зависимости скорости и высоты для времени из отрезка [0, 2].
- В ячейки Е3 и Е4 необходимо вводить начальные значения скорости и высоты – эти значения мы будем использовать в формулах как абсолютные ссылки.
- В столбцы A и D с помощью автозаполнения вводим отрезок времени [0, 2] с шагом 0,1.
- Столбец B заполняем формулой скорости:
в ячейку B10 вводим формулу скорости =$E$3–9.81*A10
копируем эту формулу в ячейки A11:A30 с помощью автозаполнения. - Столбец Е заполняем формулой высоты:
в ячейку Е10 вводим формулу скорости =$E$4+$E$3*D10–9.81*D10*D10/2
копируем эту формулу в ячейки E11:E30 с помощью автозаполнения. - по группе ячеек B10:B30 строим график «Изменение скорости тела», по группе ячеек Е10:Е30 строим график «Изменение высоты».
- После построения, редактируем графики по образцу.
в) Проведем компьютерный эксперимент:
- введем начальные значения скорости и высоты;
- проведем анализ графиков зависимости
- определим скорость и высоту в заданный момент времени
- определим время движения тела до падения и т.д.
Компьютерная модель движения тела, брошенного вертикально вверх.
5. Задачи, содержащие условие
Для решения задач, в которых в зависимости от выполнения какого-либо условия нужно выполнить разные действия используется функция проверки условия – функция ЕСЛИ.
Общий вид функции ЕСЛИ:
ЕСЛИ (<условие>; <выражение1>; <выражение2>)
Условная функция, записанная в ячейку таблицы, выполняется так:
если условие истинно, то значение данной ячейки определяется значением <выражение1>, в противном случае – значением <выражение2>.
Условием функции ЕСЛИ является логическое выражение – выражение, записанное с помощью одного из знаков отношения: <, >, <=, >=, =, < >. Такие выражения еще называют простыми условиями, например: A2>=15; B2=$C$2.
Если в задаче требуется проверить несколько условий, то используется составное условие, полученное из нескольких простых с помощью логических операций: И, ИЛИ, НЕ, например: A2>=15 И B2=$C$2; M15>N15 ИЛИ $D$2< > $K$12.
Результатом вычисления логического выражения являются логические величины ИСТИНА или ЛОЖЬ.
Особенности записи логических выражений в Excel:
- простое условие записывается в обычном виде;
- при записи составного условия сначала записывается имя логической операции (И, ИЛИ, НЕ), а затем в круглых скобках через «;» перечисляются операнды – простые условия, входящие в составное.
Примеры: И(A2>=15; B2=$C$2), ИЛИ(M15>N15; $D$2< > $K$12)
Задача №1
«Студенты сдают зачет, который предусматривает систему оценивания «Зачет» и «Незачет». Зачет ставится, если из 10 вопросов студент верно ответил больше, чем на половину вопросов, в противном случае ставится незачет. Надо автоматизировать процесс выставления зачета».
Решение:
- заполнить таблицу по образцу;
- в ячейках столбца M вычислить общее количество баллов с помощью автосуммирования;
- в ячейку N3 ввести формулу =ЕСЛИ(M3>=6;“Зачет”;“Незачет”)
- скопировать эту формулу в ячейки N с помощью автозаполнения;
- проанализировать полученный результат.
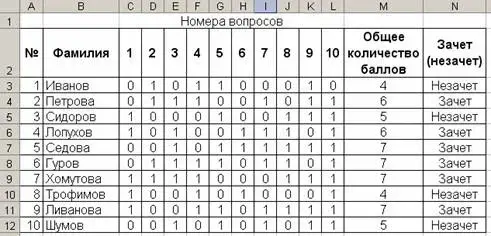
Задание. Дополните таблицу столбцом, в котором отражается получит ли студент стипендию по итогам зачета. Получают стипендию студенты, чей общий балл больше среднего общего балла по группе (используйте функцию СРЗНАЧ).
Задача №2.
«Даны коэффициенты a, b, c квадратного уравнения (a¹0). Определить, имеет ли это уравнение действительные корни или нет».
Решение:
В ячейку Е2 вводим формулу дискриминанта: =B3*B3-4*B2*B4
В ячейку G2 вводим формулу:
=ЕСЛИ(E2<0;"Действительных корней нет";"Уравнение имеет действительные корни")
Для получения результатов необходимо в ячейки B2, B3, B4 ввести исходные коэффициенты уравнения.
Задание. Дополните таблицу, чтобы при наличии корней уравнения они вычислялись.
Задача №3
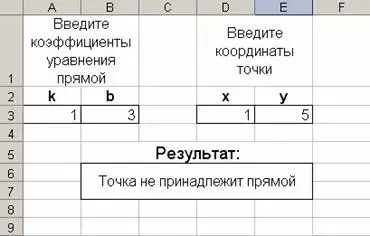
«Даны коэффициенты k и b уравнения прямой y=kx+b и даны координаты (x,y) точки на плоскости. Определить, принадлежит ли она данной прямой или нет».
Решение
В ячейку В6 вводим формулу:
=ЕСЛИ($A$3*$D$3+$B$3=$E$3;"Точка принадлежит прямой";"Точка не принадлежит прямой")
Для получения результатов необходимо в ячейки A3 и B3 ввести исходные коэффициенты прямой, а в ячейки D3 и E3 ввести исходные координаты точки.
Задание. Изменить условие в ячейке B6 так, чтобы определялось, пересекает ли данная прямая какую-либо ось (OX или OY) в данной точке.
Задача №4
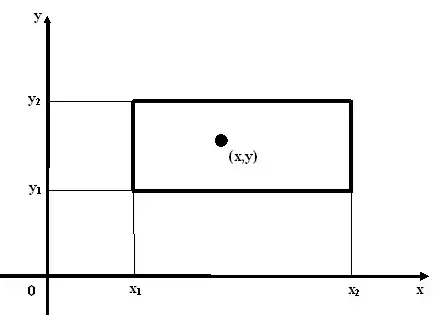
«Даны координаты вершин прямоугольника (х1,y1), (х1,y2), (х2,y1), (х2,y2), расположенного в первом квадранте, со сторонами, параллельными осям координат (0<x1<x2, 0<y1<y2), и даны координаты точки (х,y). Определить, лежит ли эта точка внутри прямоугольника (включая границы) или нет».
Решение:
Если точка с координатами (x,y) лежит внутри прямоугольника или на его границе, то должны выполняться следующие условия:
x ³ x1 и x £ x2; y ³ y1 и y £ y2.
В ячейку G4 вводим формулу:
=ЕСЛИ(И($A$7>=$A$3;$A$7<=$C$3;$B$7>=$B$3;$B$7<=$D$3);"Точка лежит внутри прямоугольника";"Точка не лежит внутри прямоугольника")
Получаем следующую таблицу:
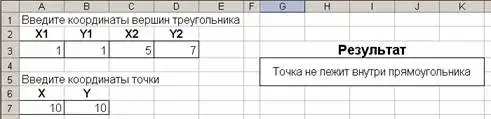
Для получения результатов необходимо в ячейки A3, B3, C3, D3 ввести исходные координаты вершин треугольника, а в ячейки A7, B7 ввести исходные координаты точки.
Задание. Измените таблицу так, чтобы определялась принадлежность точки окружности (кругу) радиуса R c центром в точке (a, b).
Задача №5
Пять абонентов звонят из города А в город Б. Если телефонный междугородный звонок был произведен в выходные дни (суббота, воскресенье), или в праздничные дни, или в будние дни с 20 часов вечера до 8 часов утра, то он рассчитывается по льготному тарифу со скидкой 50%, в другое время льгот нет. Подсчитать, сколько каждый из пяти абонентов должен заплатить за переговоры.
Примечание: Для простоты считаем, что все переговоры идут либо по обычному, либо по льготному тарифу.
Решение:
Используем заранее подготовленную таблицу стоимости телефонных переговоров. Если звонок производится по льготному тарифу, то должно выполняться условие:
День недели = “Суббота” ИЛИ День недели = “Воскресенье” ИЛИ Праздник = “Да” ИЛИ Время начала переговоров >= 20 ИЛИ Время начала переговоров <= 8.
В ячейку G3 заносим формулу и копируем в ячейки G4:G8:
=ЕСЛИ(ИЛИ(C3=“Суббота”;С3=“Воскресенье”;D3=“Да”;E3>=20;E3<=8);D$1*F3;$B$1*F3)
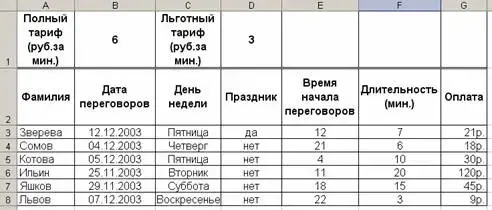
Задание. Дополнить таблицу столбцами «Скидка» и «Оплата со скидкой». Скидка в размере 8% предоставляется, если длительность разговора в будний день составила 30 минут.