Урок по алгебре и началам анализа в 10-м классе по теме "Решение простейших тригонометрических неравенств"
Цели урока:
- Показать алгоритм решения тригонометрических неравенств с использованием единичной окружности.
- Научить решать простейшие тригонометрические неравенства.
- Содействовать развитию математического мышления учащихся.
- Побуждать учащихся к преодолению трудностей в процессе умственной деятельности.
- Побуждать учащихся к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.
Знания и навыки учащихся:
- Знать алгоритм решения тригонометрических неравенств;
- Уметь решать простейшие тригонометрические неравенства;
Оборудование: интерактивная доска, презентация к уроку (Приложение 1), карточки с заданиями самостоятельной работы.
ХОД УРОКА:
I этап. Организационный момент (2 мин)
1. Вводная беседа учителя.
2. Сообщение темы и целей урока.

3. Сегодня в течение всего урока каждый будет оценивать свою работу и работу соседа в паре. (Выдаются оценочные листы)
Оценочный лист учащегося
Фамилия, Имя ____________________
|
Д/з
|
Выполнение задания по единичной окружности |
Заполнить пропуски в предложениях |
Работа по закреплению |
Самостоятельная работа |
Итоговая оценка |
|
| Оценка |
II этап. Домашнее задание (2 мин)
- Началом сегодняшнего урока станет проверка той части домашнего задания, которая нам будет помощницей при изучении нового материала. Вы дома должны были заполнить таблицу некоторых значений арксинуса и арккосинуса. Эти значения arcsin и arccos будут нам нужны при решении тригонометрических неравенств. Выполните взаимопроверку домашней работы, используя таблицу ответов на доске, и оцените работу товарища в оценочном листе.

III этап. Актуализация (8 мин)
- Давайте вспомним, что такое единичная окружность, радианная мера угла и как связан угол поворота точки на единичной окружности с радианной мерой угла.

(Работа по страницам презентации 1-4)
- Выполним задание, которое поможет нам вспомнить, как связаны между собой значения тригонометрических функций и угол поворота на единичной окружности

- Проверку задания каждый выполняет самостоятельно, оценка выставляется в оценочный лист. (Выполняется проверка задания)

- А теперь сделаем обобщение. Вы должны выполнить следующее задание: заполнить пропуски в предложениях и переписать их в тетрадь.
На единичной окружности значения косинуса различных углов располагаются на линии косинуса, которая находится на оси … .
Значения синуса различных углов располагаются на …, которая находится на … .
- Давайте выполним фронтальную проверку, и выставим оценки за задание в оценочные листы. (Один из учащихся вызывается к доске, чтобы вписать пропущенные слова)
IV этап. Объяснение нового материала (12 мин)
- Чтобы решить неравенство соs x > 1/2 , нужно выяснить, какие точки единичной окружности имеют абсциссу, большую 1/2. Абсциссу, равную 1/2, имеют две точки единичной окружности А и В. Точка В
получается поворотом точки Р (1; 0) на угол - arccos 1/2 = - ![]() /3. Точка А получается поворотом на угол arсcos 1/2 =
/3. Точка А получается поворотом на угол arсcos 1/2 = ![]() /3. Абсциссу, большую 1/2 имеют все точки дуги единичной окружности, лежащие правее прямой cos x = 1/2. Таким образом, решениями неравенства соs x > 1/2 являются все числа х из промежутка
-
/3. Абсциссу, большую 1/2 имеют все точки дуги единичной окружности, лежащие правее прямой cos x = 1/2. Таким образом, решениями неравенства соs x > 1/2 являются все числа х из промежутка
-![]() /3 < x <
/3 < x < ![]() /3. Учитывая периодичность косинуса, множество всех решений неравенства получаем добавлением к
найденным значениям чисел вида 2
/3. Учитывая периодичность косинуса, множество всех решений неравенства получаем добавлением к
найденным значениям чисел вида 2![]() n, где n
n, где n ![]() Z. Приходим к ответу:
Z. Приходим к ответу:
-![]() /3 + 2
/3 + 2![]() n < x <
n < x < ![]() /3.+ 2
/3.+ 2![]() n, где n
n, где n ![]() Z
Z
(Учитель объясняет материал, выполняя все необходимые построения на заготовке единичной окружности на доске)
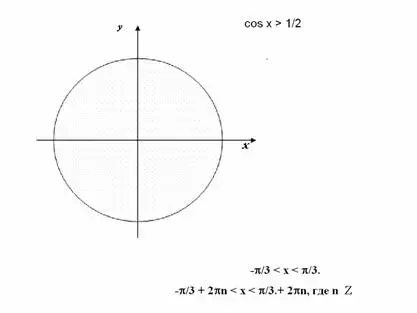
- Давайте теперь вместе разберем последовательность решения неравенств вида соs x < а и соs x > a по данным схемам. (Учитель проводит совместно с учащимися рассуждения по решению неравенств, учащиеся делают записи в тетрадях)

- Разберем последовательность решения неравенств вида sin x > a и sin x < a. (Учитель проводит совместно с учащимися рассуждения по решению неравенств, учащиеся делают записи в тетрадях.)

V этап. Практическая часть (12 мин)
- Для отработки и закрепления теоретических знаний выполним небольшие задания - решение простейших тригонометрических неравенств - несколько учащихся по очереди на доске, остальные в тетради. Оценивать эту работу буду я. (Используется заготовка единичной окружности на доске и таблица некоторых значений арксинуса и арккосинуса из домашнего задания)
№ 648 (1, 2), № 649 (1), № 650 (1, 2), № 651 (3).
- По результатам работы выставляются оценки в оценочные листы.
VI этап. Самостоятельная работа (5 мин)
- А теперь каждый из вас может показать, что он запомнил с сегодняшнего урока. Для этого необходимо выполнить небольшую самостоятельную работу.
1.
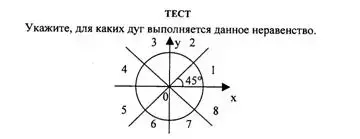
| Дуги |
Неравенство |
||
|
sin t < |
sin t > - |
cos t < - |
|
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
|
6 |
|||
|
7 |
|||
|
8 |
|||
2. Опишите алгоритм решения простейших тригонометрических неравенств, расставив правильно последовательность действий.
Чтобы решить простейшее тригонометрическое неравенство нужно:
- Найти концы этой дуги, помня, что обход совершается против часовой стрелки от меньшего числа к большему.
- Провести прямую к линии соответствующей функции
- Выделить дугу, на которой лежат решения неравенства
- Прибавить к концам интервала числа равные периоду функции
VII этап. Домашнее задание (2 мин)
- Подготовить творческую работу к уроку - семинару на тему «История тригонометрии»
- № 648 (3,4), № 650 (3, 4)
VIII этап. Итог урока (2 мин)
- Последнюю оценку за самостоятельную работу учащиеся выставляют в парах друг другу и подсчитывается средний бал. (Ключ к заданию 1 и алгоритм приведены на доске)

- А теперь подведем итог урока.
- Что нового мы сегодня узнали?
- Из каких действий состоит алгоритм решения простейших тригонометрических неравенств?
- Сдайте ваши оценочные листы. (Выставление оценок в журнал).
- Спасибо за урок!