Проблемы и подходы к обучению решения математических задач
Проблемы и подходы к обучению решения математических задач.
Одна из самых распространенных школьных проблем - проблема учебного материала, который не соответствует поставленным целям обучения. Яркий пример - задачи по математике в начальной школе.
Учебная цель - научить решать задачи по математике.
Результат - большой процент детей не умеют решать задачи, не воспринимают условия, правила решения, порядок действий, смысла и содержание задач.
На успешное овладение умением решать задачи оказывает влияние не само по себе количество решаемых задач, а прежде всего планомерная углубленная работа по всестороннему анализу задачи.
Прежде всего, хотелось бы представить некоторые проблемы в обучении решению задач, которые были выявлены в процессе моей многолетней работы в начальной школе.
Проблемы в обучении решению задач:
1. Проблема классификации задач начальной школы.
Существующие классификации задач не помогают выявлению их смысла, т. е. классификации типа: "в одно действие, в два действия, простые, сложные, с косвенным вопросом и др." не помогают детям решать эти задачи.
2. Проблема записи условий задачи.
Краткая запись условия не показывает структурные связи данных задачи, а отображение условия с помощью отрезков требует развитого абстрактного мышления и не воспринимается слабыми детьми. Отсюда возникают трудности в определении путей решения задачи.
3. Проблема проверки правильности решения задачи.
Обычно проверяют не решение задачи, а правильность математических действий в этой задаче, что далеко не одно и то же.
Проверку необходимо производить до начала математических действий, путём проговаривания условия по записанной модели и сличения его с текстом задачи, решить другим способом, составлять и решать обратные задачи.
4. Проблема последовательности действий ученика при решении задач.
Таких правил, памяток, описаний, алгоритмов существует много, но они не работают без решения первых трех проблем.
Общеизвестно, что существует 2 подхода к решению задач:
- частный подход - знакомство с алгоритмом и доведение его до автоматизма;
- общий подход - заключается в знании, что такое задача, знании этапов решения задачи и умении выполнять эти этапы.
Этапы решения задач. Таблица № 1.
|
Этапы решения задач |
Цель этапа |
Приемы выполнения этапа |
| 1.Анализ содержания задачи. | Понять, выделить величины, отношения, зависимости. |
Разбиение на смысловые части, перефразировка (разъяснение слов, замена терминов, убрать несущественные слова).
Моделирование, таблица. |
| 2.Поиск плана решения. | Установить зависимость и связь между данными и искомыми. | По модели. |
| 3.Выполнение плана решения задачи. | Выполнение плана. | По действиям, с вопросами, с пояснением, уравнением,… |
| 4. Проверка. | Связь с условием задачи. | Составить и решить обратные задачи, решение другим способом, методом, прикидка определенного смысла составленного выражения по ходу решения. |
Анализируя содержание задачи, очень важно научить детей составлять модели задачи.
Модель - это в некотором смысле копия, она может быть упрощена и позволяет лучше, полнее изучать оригинал.
Модель строят на 1-м этапе решения задачи для того, чтобы понять задачу.
Модели бывают 3-х видов:
- Вещественные (предметные): - из оригиналов (тетради, карандаши, конфеты…); - из копий, внешне похожих на оригиналы (утята, котята, огурцы…); - из фишек без сохранения сходства с оригиналами.
При вещественном моделировании выполняются конкретные действия руками.
Рисунок № 1.

Рисунок № 2.

- Знаковые (схема);
- Графические (рисунок и чертеж).
Графические модели:
Задача № 1.
У Иры 5 шаров, что на 2 меньше, чем у Светы. Сколько шаров у Светы?
Задача № 2.
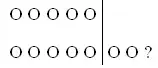
В гараже 5 легковых машин и еще 2 грузовые подъехали. Сколько стало машин?
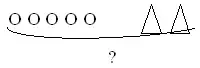
Задача № 3
Блокнот стоит 90 р., открытка 50 р. На сколько блокнот дороже открытки?

Схемы позволяют представить содержание задачи в наглядной, легко воспринимаемой форме, существенно облегчают поиск ее решения.
Задача № 4
У Маши, Тани и Кати 8 марок. У Маши 2 марки, а у Тани 3 марки. Сколько марок у Кати?
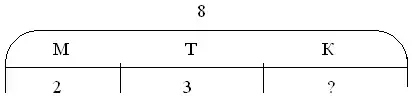
Целый отрезок на схеме обозначает число всех марок, а части отрезка - число марок у Маши, Тани и Кати . По схеме видно, что для нахождения числа марок у Кати надо из всех марок вычесть число марок Маши и Тани.
В задачах, в которых рассматриваются отношения "больше на …", "меньше на …" схемы имеют другой вид.
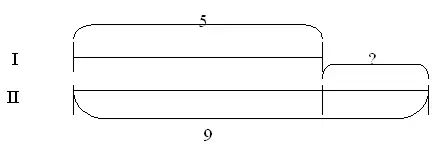
Задача № 5
В одном доме 5 этажей, а в другом 9. На сколько этажей во 2-м доме больше, чем в 1-м?
Методы решения задач: арифметический, алгебраический, графический, практический, логический, смешанный, табличный.
Поиск плана решения задач
Существуют 2 вида разбора задач: синтетический (рассуждения надо вести от данных задач к ее вопросу), аналитический (от вопроса задачи - к данным).
При аналитическом способе решения задачи выясняется, что нужно предварительно узнать, чтобы ответить на вопрос задачи. Чтобы помочь детям вести рассуждения аналитическим способом, можно использовать прием, называемый "деревом рассуждений". Суть его состоит в том, что по ходу рассуждений строится схема, которая помогает увидеть, какие простые задачи следует выделить и каким будет план решения данной составной задачи.
Задача. С одного поля собрали 240 ц картофеля, с другого в 2 раза меньше. 3-ю часть картофеля, собранного со 2-го поля, разложили в мешки по 50 кг каждый и увезли с поля поровну на 2-х машинах. Сколько мешков положили на каждую машину?
Модель задачи:
Собрали: 1 п. - 240 ц
2 п. - ? ц, в 2 раза <
Разложили: 1/3 со 2 п. по 50 кг - ? м.
Увезли на 2-х маш. по ? м.
Аналитический способ разбора задачи.
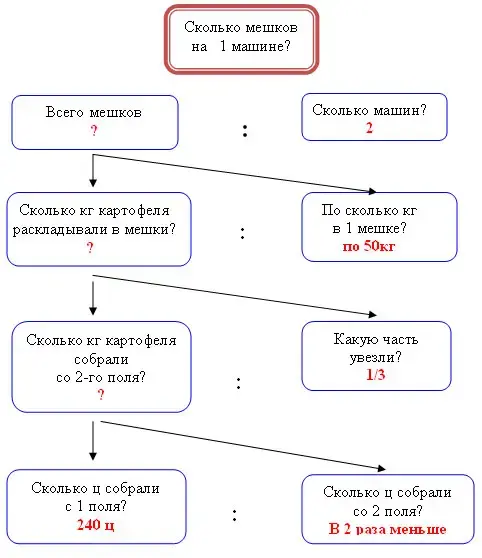
Синтетический способ характеризуется тем, что основным вопросом при поиске решения задачи является вопрос о том, что можно найти по двум или нескольким известным в тексте задачи числовым значениям. По вновь полученным числовым значениям и другим известным в задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос составной задачи. Иными словами, суть этого способа состоит в вычленении простой задачи из предложенной составной и решении ее.
Для формирования умения вычленять простую задачу из составной целесообразно предлагать детям решать серии (блоки) задач с нарастающей сложностью. Быстрое решение таких задач дает возможность быстрого узнавания простых задач в составе составных.
Синтетический способ разбора задач
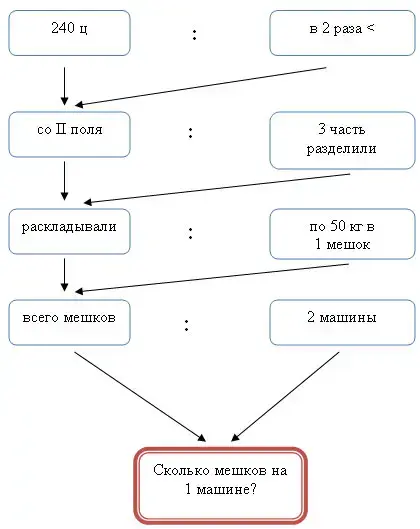
См. приложение.