Методические рекомендации "Решение геометрических задач"
Методические рекомендации "Решение геометрических задач"
Решение задач - один из основных этапов усвоения учащимися системы математических знаний, в частности геометрических понятий и связей между ними. Решая геометрические задачи, учащиеся развивают творческие способности, самостоятельное мышление, приобретают навыки практического применения теоретических положений геометрии. Педагогическая практика показывает, что решение задач, не объединенных общими приемами, не дает хороших результатов, вызывает большие затруднения у учащихся.
При планировании урока учителю необходимо обратить внимание учащихся на теоретический материал, необходимый при решении задачи, переосмыслить его содержание на практике. Такой методический прием подготовит учащихся к успешному восприятию и осмыслению конкретной задачи, к осознанному применению теории на практике, будет способствовать закреплению ранее изученного материала, приобретенные математические знания станут более прочными.
При решении математической задачи можно выделить следующие этапы:
- изучение условия задачи;
- анализ решения задачи (поиск путей решения);
- выбор оптимального пути решения задачи;
- решение задачи;
- исследование полученного результата.
Часто учащиеся опускают последний шаг приведенного алгоритма, что приводит к неверному результату.
При решении геометрических задач на первых уроках целесообразно предложить учащимся следующий алгоритм решения:
- Изучить условие задачи. Выполнить эскиз рисунка, соответствующий условию данной задачи.
- Уяснить, что необходимо найти в задаче и что для этого необходимо знать.
- Из системы опорных задач выделить часто повторяющиеся задачи (желательно сопроводить иллюстрацией), которые будут входить в ход решения данной задачи.
- Выяснить, какие из ранее изученных задач могут быть полезны при решении данной задачи.
- Учитывая предыдущий шаг, переформулировать данную задачу. Попробовать решить ее.
Зная систему опорных задач, учитель четко планирует необходимость использования конкретной опорной задачи при решении данной задачи. Это дает возможность обучить учащихся приему "разложения" сложной задачи на более простые составляющие задачи.
При решении задач используются аналитический и синтетический методы.
При аналитическом методе решения задач учащиеся должны четко представлять, что анализ состоит в том, что рассуждения ведутся от искомого к данным. Ведущий вопрос - "Что надо знать, чтобы ответить на главный вопрос задачи?". Проводя анализ задачи, необходимо обращать внимание учащихся на то, что иногда условия задачи дают подсказку на очередной ведущий вопрос. При синтетическом методе решения задач учащиеся должны понимать, что синтетические рассуждения - это рассуждения с последующим переходом (с помощью логических умозаключений) от данных условий задачи к ее заключению. Ведущий вопрос в этом случае - "Что мы можем узнать исходя из данных условий задачи?".
Покажем, как применяется анализ и синтез на примере конкретной задачи.
Задача (№142, учебник "Геометрия 7-9", Л.С.Атанасян и др., Москва, "Просвещение", 2003 г.): Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая AB пересекает отрезок CD в точке O. Докажите, что: а) угол ADB равен углу ACB; б) DO=OC.
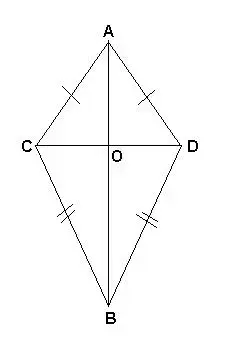
<Рисунок 1>
Синтетическое рассуждение и решение задачи:

<Рисунок 2>
Решая задачу с помощью синтетических рассуждений, мы последовательно выбираем зависимые между собой и необходимые для решения задачи пары данных в условии величин, проверяем каждый раз, приближаемся ли мы к получению конечного результата при составлении определенных комбинаций.
Аналитическое рассуждение и решение задачи

<Рисунок 3>
Рассмотрев решение задачи двумя предложенными методами, следует обратить внимание учащихся на то, что в последовательности цепи умозаключений анализ и синтез неотделимо связаны между собой. Так, проводя анализ, т.е. следуя от вопроса задачи необходимо обращать внимание на то, что иногда данные условия задачи предполагают ответ на очередной ведущий вопрос. И, наоборот, следуя синтетическим методом, т.е. комбинируя данные задачи, мы постоянно имеем в виду вопрос, на который необходимо дать ответ. Таким образом, следует вывод, что органическое соединение анализа и синтеза при решении задач представляет собой единый аналитико-синтетический метод.