Решение задач "Электростатика. Потенциальная энергия электрического взаимодействия"
- Сила Кулона.
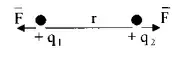
![]() ;
; ![]() - диэлектрическая проницаемость.
- диэлектрическая проницаемость.
![]() ;
;
- Потенциальная (электростатическая) энергия взаимодействия зарядов.
![]() - может быть и положительной и отрицательной.
- может быть и положительной и отрицательной.
Если есть система электрических точечных зарядов qi…….qg, то
![]() .
.
Методические указания по решению задач.
Решая задачи целесообразно использовать следующие методические указания.
- Вникнув в условие задачи, сделать краткую запись условия, выразить все данные в СИ и, где это только возможно, сделать схематичный чертеж или рисунок, поясняющий содержание задачи.
- Выяснив, какие физические законы лежат в основе данной задачи, решить ее в общем виде, т.е. выразить искомую физическую величину через заданные в задаче величины (в буквенных обозначениях, без подстановки числовых значений в промежуточные формулы).
- Проверив правильность общего решения, подставить числа в окончательную формулу и указать единицу искомой величины, проверив правильность ее размерности. Проверить достоверность ответа.
1. Два разноименных заряда q1= 2*10-9Кл и q2= -3*10-9Кл находятся на расcтоянии r1=1м. Какую работу необходимо совершить, чтобы раздвинуть эти заряды на r2= 2м.
|
Дано |
Решение |
|
q1= 2*10-9Кл
q2= -3*10-9Кл r1=1м. r
|
А W А |
| А |
|
| Ответ: А |
|
2.Четыре точечных положительных заряда находятся в вершинах квадрата со стороной а. Найдите потенциальную энергию W![]() всей системы.
всей системы.
|
Дано |
Рисунок |
Решение |
|
|
q
a =r |
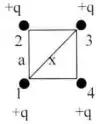 |
x = r W W W W |
|
| W |
|||
| Ответ: W |
|||
3. Два отрицательных и два положительных заряда находятся в вершинах квадрата со стороной а, как показано на рисунке. Найдите потенциальную энергию всей системы.
|
Дано |
Рисунок Решение | |
|
-q
+q a |
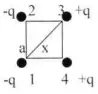 |
x=r W W W W |
| W |
||
| Ответ: W |
||
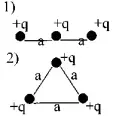
4. Какую работу необходимо совершить, чтобы три положительных заряда q, находящиеся в вакууме на одной прямой, на расстоянии а друг от друга, расположить в вершинах равностороннего треугольника.
|
Дано |
Рисунок |
Решение |
|
q a
|
 |
А
А |
| А |
||
| Ответ: А |
||
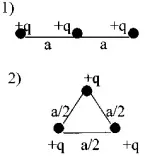
5. Определить работу, которую нужно совершить, чтобы три положительных заряда q, находящиеся в вакууме на одной прямой, на расстоянии а друг от друга, расположить в вершинах равностороннего треугольника со стороной а/2.
|
Дано |
Рисунок |
Решение |
|
q a
|
 |
А
А |
| А |
||
| Ответ: А |
||
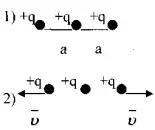
6. Три маленьких положительно заряженных шарика заряда q каждый удерживаются вдоль прямой на расстоянии а друг от друга двумя нитями. Какую максимальную кинетическую энергию приобретет крайний шарик, если обе нити одновременно пережечь.
|
Дано |
Рисунок |
Решение |
|
q
a
|
 |
По закону сохранения энергии:
Е 1) Е 2) Е
E |
| E |
||
| Ответ: E |
||
7. Три маленьких положительно заряженных шарика, массой m и зарядом q каждый соединены нитями и находятся на расстоянии а друг от друга. Определить максимальную скорость крайнего шарика №1, если одну из нитей пережечь.
|
Дано |
Рисунок |
Решение |
|
q
m a |
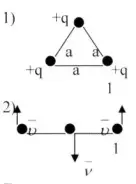
Если продолжить наблюдать процесс, то увидим колебательную систему. |
По закону сохранения импульса общий импульс системы равен нулю и до и после пережигания нити:
2m
По закону сохранения энергии: Е Е Е 3k
|
| Ответ: V |
||
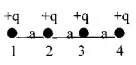
8. Четыре точечных положительных заряда q расположены на расстоянии а на одной прямой. Определите полную потенциальную энергию системы.
|
Дано |
Рисунок |
Решение |
|
q
a |
 |
W W W W |
| W |
||
| Ответ: W |
||