Построение графиков линейной и квадратичной функций
Данная статья не содержит графических иллюстраций. Поэтому знакомиться с ее содержанием будет удобнее, имея под рукой лист бумаги и карандаш.
1. Линейная функция
При изучении линейной функции ![]() на уроках алгебры в 7-м классе учащиеся довольно успешно осваивают способ построения прямой по двум
точкам. При этом составляется таблица, в которой задаются значения х и вычисляются соответствующие значения y. Однако при построении прямой часто допускаются неточности: из-за того,
что выбранные точки очень близко расположены друг к другу, построенная прямая "уходит в сторону". Построить график линейной функции можно гораздо быстрее, если заметить определенные закономерности.
Рассмотрим примеры.
на уроках алгебры в 7-м классе учащиеся довольно успешно осваивают способ построения прямой по двум
точкам. При этом составляется таблица, в которой задаются значения х и вычисляются соответствующие значения y. Однако при построении прямой часто допускаются неточности: из-за того,
что выбранные точки очень близко расположены друг к другу, построенная прямая "уходит в сторону". Построить график линейной функции можно гораздо быстрее, если заметить определенные закономерности.
Рассмотрим примеры.
Пример 1. Построить график функции ![]() .
.
Решение Составим таблицу значений функции.
| Порядковый № | 1 | 2 | 3 | 4 | 5 |
| x | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -1 | 1 | 3 | 5 |
Первая точка выбирается традиционно - точка пересечения прямой с осью ординат. А дальше обратим внимание, что разность значений функции ![]() , т.е. совпадает со значением углового коэффициента заданной функции. А значит, для построения точек на координатной плоскости вся информация заложена в коэффициентах заданной линейной
функции. Алгоритм построения точек следующий:
, т.е. совпадает со значением углового коэффициента заданной функции. А значит, для построения точек на координатной плоскости вся информация заложена в коэффициентах заданной линейной
функции. Алгоритм построения точек следующий:
- строим первую точку
 ;
; - переносим ее на 1 единицу вправо и две единицы вверх (это вторая точка, принадлежащая прямой):
- вторую точку снова перемещаем на 1 единицу вправо и две единицы вверх и получаем третью точку искомой прямой;
- далее все повторяется любое число раз.
Пример 2. Построить график функции ![]() .
.
Решение Первая точка имеет координаты ![]() . Каждая следующая получается из предыдущей смещением на 1 единицу
вправо и на 3 единицы вниз.
. Каждая следующая получается из предыдущей смещением на 1 единицу
вправо и на 3 единицы вниз.
Рассмотрим теперь случай, когда угловой коэффициент линейной функции задается дробью.
Пример 3. Построить график функции ![]() .
.
Решение Составим таблицу значений функции. Чтобы получить точки прямой с целочисленными координатами, возьмем значения х, кратные трем. Ну. а первая точка, по-прежнему, - точка пересечения прямой с осью ординат.
| x | 0 | 3 | 6 | 9 | 12 |
| y | -4 | -2 | 0 | 2 | 4 |
Построим точки на координатной плоскости. Видно, что каждая следующая точка получается из предыдущей сдвигом на 3 единицы вправо и 2 единицы вверх. Проводим прямую.
Пример 4. Построить график функции ![]() .
.
Решение Первая точка имеет координаты ![]() . Заметим, что угловой коэффициент прямой
. Заметим, что угловой коэффициент прямой ![]() . Значит, каждая следующая точка прямой будет получена из предыдущей смещением на 5 единиц вправо и на 4 единицы вниз. Строим точки и проводим прямую.
. Значит, каждая следующая точка прямой будет получена из предыдущей смещением на 5 единиц вправо и на 4 единицы вниз. Строим точки и проводим прямую.
Обратите внимание, что в случае дробного углового коэффициента линейной функции знаменатель дроби указывает количество единиц для перемещения точки вправо, а числитель - количество единиц, на
которые переместится точка вверх (при ![]() ) или вниз (при k<0).
) или вниз (при k<0).
2. Квадратичная функция
2.1. С графиком квадратичной функции ![]() учащиеся знакомятся еще в седьмом классе. При этом, для построения параболы,
как правило, записывается таблица значений функции для
учащиеся знакомятся еще в седьмом классе. При этом, для построения параболы,
как правило, записывается таблица значений функции для ![]() , затем полученные точки строят на координатной прямой и рисуют параболу.
Более продвинутые ученики записывают таблицу только для
, затем полученные точки строят на координатной прямой и рисуют параболу.
Более продвинутые ученики записывают таблицу только для ![]() , строят полученные точки и проводят правую ветвь параболы. Затем,
воспользовавшись симметрией графика относительно оси ординат, строят точки параболы для
, строят полученные точки и проводят правую ветвь параболы. Затем,
воспользовавшись симметрией графика относительно оси ординат, строят точки параболы для ![]() и рисуют вторую ветвь параболы.
и рисуют вторую ветвь параболы.
Записи таблицы можно избежать, если заметить одну закономерность в расположении указанных точек. Посмотрим таблицу значений функции ![]() :
:
| 0 | 1 | 2 | 3 | |||
| 0 | 1 | 4 | 9 | |||
В третьей строке таблицы записана разность двух последующих значений функции. Видно, что полученные числа образуют последовательность нечетных чисел ![]() (легко убедиться, что эта закономерность выполняется и далее, например,
(легко убедиться, что эта закономерность выполняется и далее, например, ![]() ). Этот факт легко запоминается. А с
учетом этой закономерности построить характеристические точки параболы можно так:
). Этот факт легко запоминается. А с
учетом этой закономерности построить характеристические точки параболы можно так:
- первая точка - начало координат;
- вторая точка получается из первой смещением на одну единицу вправо и на одну единицу вверх;
- третья получается смещением второй точки на один вправо и три вверх;
- четвертая точка получается переносом третьей на один вправо и пять вверх;
- затем строятся точки левой ветви параболы за счет симметрии графика относительно оси ординат.
Остается провести плавную линию через полученные точки, и парабола построена.
2.2. Перейдем теперь к квадратичной функции вида ![]() , которая изучается уже в восьмом классе. Учащиеся узнают, что
коэффициент а определяет направление ветвей параболы, а также растяжение или сжатие графика вдоль оси ординат. А для построения графика все равно просчитывают координаты точек. Но без этого
можно обойтись, если знать указанную выше закономерность построения точек параболы
, которая изучается уже в восьмом классе. Учащиеся узнают, что
коэффициент а определяет направление ветвей параболы, а также растяжение или сжатие графика вдоль оси ординат. А для построения графика все равно просчитывают координаты точек. Но без этого
можно обойтись, если знать указанную выше закономерность построения точек параболы ![]() . И если для нее сдвиг точек вдоль оси OY
задавался последовательностью чисел
. И если для нее сдвиг точек вдоль оси OY
задавался последовательностью чисел ![]() , то для функции
, то для функции ![]() эта
последовательность чисел будет
эта
последовательность чисел будет ![]() .
.
Пример 5. Построить график функции ![]() .
.
Решение Графиком функции служит парабола, ветви которой направлены вниз, а вершина находится в начале координат. Для построения других точек параболы вспомним про нечетные
числа ![]() , умножим их на
, умножим их на ![]() , получаем последовательность чисел
, получаем последовательность чисел ![]() Знак
Знак ![]() говорит о том , что смещение точек будет сделано вниз. На словах
алгоритм построения звучит так: от начала координат одна единица вправо и две вниз; от новой точки одна единица вправо и шесть вниз; строим точки, симметричные полученным относительно оси ординат;
проводим параболу.
говорит о том , что смещение точек будет сделано вниз. На словах
алгоритм построения звучит так: от начала координат одна единица вправо и две вниз; от новой точки одна единица вправо и шесть вниз; строим точки, симметричные полученным относительно оси ординат;
проводим параболу.
Пример 6. Построить график функции ![]() .
.
Решение Графиком функции - парабола, ветви которой направлены вверх. Вершина параболы находится в начале координат. Для построения других точек воспользуемся
последовательностью ![]() При
При ![]() получаем следующий порядок перемещений
вдоль оси ординат
получаем следующий порядок перемещений
вдоль оси ординат ![]() . Строим точки на координатной плоскости: от точки
. Строим точки на координатной плоскости: от точки ![]() 1 клетка вправо и полклетки вверх, от полученной точки снова одна клетка вправо и полторы клетки вверх, потом от новой точки опять одна клетка вправо и две с половиной клетки вверх и
т.д. (ясно, что в указанном случае за единичный отрезок на осях координат принимается одна клеточка в тетрадном листе). Затем строим точки левой ветви параболы за счет симметрии графика относительно
оси OY и рисуем параболу.
1 клетка вправо и полклетки вверх, от полученной точки снова одна клетка вправо и полторы клетки вверх, потом от новой точки опять одна клетка вправо и две с половиной клетки вверх и
т.д. (ясно, что в указанном случае за единичный отрезок на осях координат принимается одна клеточка в тетрадном листе). Затем строим точки левой ветви параболы за счет симметрии графика относительно
оси OY и рисуем параболу.
2.3. В 9-м классе учащиеся изучают квадратичную функцию ![]() . Для построения ее графика с учетом выше сказанного
можно применять следующий алгоритм:
. Для построения ее графика с учетом выше сказанного
можно применять следующий алгоритм:
- найти координаты вершины параболы
 ;
; - построить в системе координат полученную точку и провести оси вспомогательной системы координат (прямые
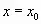 и
и 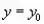 );
); - по коэффициенту а определить направление ветвей параболы;
- построить во вспомогательной системе координат характеристические точки функции
 , следуя алгоритму пункта 2.2.
, следуя алгоритму пункта 2.2. - провести плавную линию через указанные точки. График готов.
Пример 7. Построить график функции ![]() .
.
Решение Графиком функции - парабола.
- Вычисляем координаты вершины параболы:
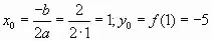 .
. - Строим точку
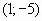 и проводим пунктиром вспомогательные оси координат (прямые проходят через указанную точку и параллельны осям ОХ
и ОY).
и проводим пунктиром вспомогательные оси координат (прямые проходят через указанную точку и параллельны осям ОХ
и ОY). - Коэффициент при х2 в данной функции равен 1. Значит, для построения характеристических точек параболы применим ряд чисел 1,3,5,…. , т.е. строим стандартную параболу, но во вспомогательной системе координат (пункт 2.1.).
- Проводим плавную линию через полученные точки. Парабола построена.
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Постройте графики указанных функций:
| 1. |
2. |
3. |
4. |
| 5. |
6. |
7. |
8. |
| 9. |
10. |
11. |
12. |