Цели урока:
- проверка и закрепление ЗУН по решению заданий из КИМов к ЕГЭ;
- закрепление навыков работы в группе;
- воспитание положительной мотивации по подготовке к экзаменам.
Ход урока
1. Организационный момент.
В классе сформированы три группы: по части A, по части B, по части C. Группы можно разбить по принципу: менее подготовленная группа, средняя группа и более сильная группа. В каждой группе выбран ведущий, он распределяет обязанности, готовит учащихся к защите заданий, выставляет групповую оценку, индивидуальную оценку, расписывается в дневниках. За основу берется один из КИМов. Каждая группа получает лист с заданиями и лист с нормами оценивания работы и планом работы. На доске заранее приготовлена таблица для ответов, по мере выполнения заданий учащиеся записывают ответы. Если группа справится с заданием раньше отведенного времени, то каждый может зарабатывать индивидуальную оценку.
2. Работа в творческих группах.
1-я группа
А1. Упростите выражение 
.
А2. Вычислите: 
.
А3. Найдите значение выражения 
.
А4. Функция задана графиком. На каком из
указанных промежутков она возрастает?
1) [-5; -1]
2) [-1; 4]
3) [-2; 2]
4) [-5; 0]
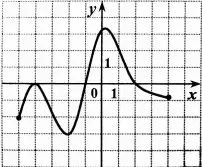
А5. Найдите производную функции 
.
А6. Найдите множество значений функции 
.
А7. Функция задана графиком. Укажите промежуток, на котором она принимает только положительные значения.
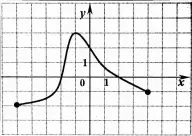
А8. Решите неравенство 
.
А9. Решите уравнение 
А10. Решите неравенство 
2-я группа
В1. Найдите значение выражения 
.
В2. Решите уравнение 
.
В3. Решите уравнение 
.
В4. Найдите значение выражения 
, если известно, что
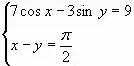
В5. Найдите значение выражения 
.
В6. Решите уравнение 
.
(Если уравнение имеет более одного корня, то в бланке ответов запишите произведение всех его корней).
3-я группа
С1. Две бригады, работая вместе, ремонтировали дорогу в течение 5 дней, а затем одна вторая бригада закончила ремонт еще за 9 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на 6 дней быстрее, чем одна вторая бригада?
С2. Найдите точки минимума функции 
С3. Решите уравнение 
.
По окончании времени учитель зачитывает верные версии, называет оценку группе. Ведущий в группе выставляет индивидуальные оценки и расписывается в дневниках.
3. Защита заданий у доски.
Представитель от каждой группы проводит анализ решенных заданий, проговаривает формулы и комментирует одно из заданий.
4. Итог урока.
Каждый пишет в тетради, затем один ученик зачитывает, все проверяют. Можно оценить еще одной оценкой.
- На сколько процентов ты готов к ЕГЭ?
- Самая трудная тема для тебя?
- При делении степеней показатели …
- Сумма логарифмов равна логарифму …
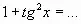
- Чему равно основание натурального логарифма?
- Количество букв в отчестве поэта Сергея Есенина?
- Из каких чисел извлекается квадратный корень?
- На какой оси располагаются нули функции?
- Дополни гласными и запиши слово к л б н.
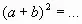
- Каким должно быть выражение под знаком логарифма?
- Какое вещество называют слезами Балтийского моря?
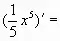
- Дополни гласными и напиши слово н т н м.
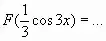
- Чему равен угловой коэффициент у касательной в точке касания?
- Дополни гласными и напиши слово д к р т р.
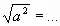
- Дополни гласными и напиши слово к з м т.
Оценки
- “5” - 18-12,
- “4” - 11-10,
- “3” - 9 и менее.
Домашнее задание. Формулы.