Цели и задачи:
1. Способствовать:
- формированию у учащихся инновационных способов учебной и познавательной деятельности;
- воспитанию эстетических качеств личности;
- развитию воображения, умению применять знания в незнакомой ситуации.
2. Сформировать понятие “площадь простой фигуры”.
3. Вывести формулы площади параллелограмма, треугольника, трапеции, квадрата (практически), используя знание формулы площади прямоугольника.
4. Закрепить формулы решением задач.
Оборудование урока:
- Ножницы;
- Геометрические фигуры из бумаги: 2 равных прямоугольных треугольника;
- 2 равные трапеции; 2 равных прямоугольника, одна сторона у которых больше
- другой в 2 раза;
- Чертежные инструменты;
- Компьютерный класс.
Методы:
- Проблемно-поисковый;
- Самостоятельной работы.
Тип урока: урок получения новых знаний, практико-ориентированный.
Ход урока
Организационный момент: повторение правил техники безопасности работы на компьютере, с ножницами.
Актуализация знаний учащихся:
Тест (с использованием компьютерной презентации)
1) Если геометрическую фигуру можно разбить на конечное число плоских треугольников, то она называется
а) сложной
б) простой
2) Какая геометрическая фигура не является простой?
а) круг
б) многоугольник
в) трапеция
3) Фигуры называются равновеликими, если у них
а) равные площади
б) равные углы
4) Формула площади прямоугольника
а)
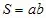
б)
5) Формула площади квадрата
а)
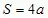
б)
Вступительная беседа. “Геометрия = землемерие”.
Цель: Объяснить необходимость вычисления площадей различных плоских фигур в связи с развитием земледелия в Египте, который образовался более пяти тысяч лет назад.
Практическая работа с использованием компьютерной презентации (Приложение), в ходе которой учащиеся получают формулы площади прямоугольного и произвольного треугольников, параллелограмма, трапеции, квадрата через его диагонали.
Задание №1. Возьмите два равных
прямоугольных треугольника с катетами 
и 
и
сложите из них прямоугольник. Зная, что площадь
прямоугольника 
, получим площадь прямоугольного
треугольника, как половину площади
прямоугольника 
, т. е. половину произведения катетов.
Задание №2. Переложите треугольники так,
чтобы получился параллелограмм. Его площадь
равна площади прямоугольника, т. е. 
.
Обозначим 
(высота), тогда площадь
параллелограмма равна 
.
Задание №3. сложите из двух прямоугольных
треугольников треугольник. Его площадь равна
площади прямоугольника, т. е. 
, где 
, 
или 
, 
.
Задание №4. разделите прямоугольник (одна
сторона которого в два раза больше другой) на две
части так, чтобы из них можно было сложить
прямоугольный треугольник. Т. к. треугольник
равнобедренный 
и равновелик с прямоугольником, то его
площадь 
.
Задание №5. Разделите прямоугольник (одна
сторона которого в два раза больше другой) на три
части так, чтобы из них можно было сложить
квадрат. Т. к. площадь квадрата равна площади
прямоугольника со сторонами 
и 
, то 
,где 
-
диагональ квадрата.
Задание №6. Сложите две равные трапеции так,
чтобы получился параллелограмм. Тогда площадь
параллелограмма 
, а площадь трапеции равна
половине площади этого параллелограмма 
.
Подведение итогов.
Теперь вы знаете, что площади простых фигур вычисляются с помощью формул:
, 
, 
, 
, 
, 
, 
.
Запишите их в тетрадь, но знайте, что есть и другие. Значит у вас впереди еще много интересных уроков.
Физминутка: (после работы на компьютере)
- Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до пяти. Повторить 4-5 раз.
- Вытянуть правую руку вперёд. Следить глазами, не поворачивая головы, за медленным движением указательного пальца вытянутой руки влево и вправо, вверх и вниз. Повторить 4-5 раз.
- В среднем темпе проделать 3-4 круговых движения глазами в правую сторону, столько же в левую сторону. Расслабив глазные мышцы, посмотреть вдаль на счет 1-6. Повторить 1-2 раза.
Закрепление
1. Поиграем?
На гранях кубика изображены простые геометрические фигуры: квадрат, прямоугольник, треугольник, прямоугольный треугольник, параллелограмм, трапеция.
Бросаем кубик и называем формулу площади фигуры, выпавшей на грани кубика.
2. Решение задач с использованием полученных формул
- Найдите площадь треугольника, если одна из его сторон a=5см, а высота, проведенная к ней, h=4см.
- Найдите площадь параллелограмма, если одна из его сторон a=6см, а высота, проведенная к ней, h=3см.
- Найдите площадь квадрата со стороной a=5см.
- Найдите площадь трапеции с основаниями a=9см и b=7см, высотой h=3см.
- Найдите площадь прямоугольного треугольника с катетами a=8см и b=3см.
- Найдите площадь квадрата, диагональ которого d=8см.
- Найдите площадь прямоугольника со сторонами 5см и 3см.
Каждый учащийся заполняет лист ответов и сдает его учителю.
Лист ответов
Работа выполнена ______________________________________
(фамилия имя, класс)
Оценка ______________
(подпись учителя)
№ задачи площадь численное значение (кв. ед. ) 1. параллелограмма 2. треугольника 3. квадрата 4. трапеции 5. прямоугольного треугольника 6. квадрата 7. прямоугольника
Затем получает домашнее задание с алгоритмом решения задачи.
Домашнее задание: п. 122-124, 126 (правила), формулы (в тетради) учить, решить задачу.
Задача: В треугольнике ABC BC=34см. перпендикуляр MN, проведенный из середины BC к прямой AC, делит сторону AC на отрезки AN=25см и NC=15см. Найдите площадь треугольника ABC.
Алгоритм решения:
- Найди по теореме Пифагора MN из треугольника MNC.
- Дострой треугольник ABC до параллелограмма ACPB.
- Докажи равенство треугольников BHM и CNM.
- Найди HN.
- Найди площадь параллелограмма (HN=h), затем площадь треугольника.
- Запиши ответ.
Итог урока. Каждый ребенок открывает компьютерную страницу, идентичную “листу ответов”, и выполняет последнее задание урока.
Чтобы убедиться в правильности решения задач, откройте все звездочки* по порядку и сверьте со своими ответами. Если всё верно, поставьте себе “5”, при одной ошибке “4”, при двух – “3”. Если ошибок больше, выучите формулы! (смотрите домашнее задание)