Урок алгебры по теме: "Графический способ решения уравнений". 8-й класс
Тип урока:
- урок-практикум.
Общеобразовательная цель:
- систематизация знаний учащихся по теме,
- формирование прочных навыков и умений при решении уравнений графическим способом,
- выработка умений применять известные знания в незнакомой ситуации,
- выработка способности учащихся к обобщению частных случаев.
Развивающая цель:
- сознательное усвоение учащимися алгебраических понятий и связей между ними,
- формирование приемов поиска решений задач с параметрами.
Воспитательная цель:
- формирование графической культуры,
- возбуждение и развитие интереса учащихся к самостоятельному творчеству.
Средства обучения:
- компьютер,
- мультимедийный проектор,
- презентация,
- дидактический раздаточный материал.
Перед уроком на экране слайд № 1
1. Организационный момент (1 минута)
(Учитель сообщает классу дату проведения урока, тему урока. На экране слайд № 3)
- Если вы хотите научиться плавать,
то смело входите в воду,
а если хотите
научиться решать задачи -
решайте их.
Д. Пойа "Математическое открытие"
Вступление.
- Мы знаем, что графический способ решения уравнений применяется довольно редко. Но существует достаточно много задач, в которых важен поиск не самих корней уравнений - их значений, а только количество корней.
Представим себе, что в середине января вас посылают в лес собирать грибы. Хотя вы отлично знаете технологию сбора грибов, вы в лес не пойдете. Опыт поколений показывает, что зимой грибы не растут. Вернемся к нашей задаче. Графическим способом можно найти количество корней, что облегчает их поиск, или доказать, что их нет, а тогда зачем решать уравнение?
Работать мы сегодня будем по следующей схеме (слайд №4):
Мы покажем связь тем изученных на предыдущих уроках, "преобразование графиков функций", "графики функций", "свойства функции", будем решать уравнения графическим способом, находить количество корней уравнения с помощью графического метода, а также познакомимся с решением уравнения с параметром графическим способом.
2. Проверка знаний учащихся по теме "Функции. Графики функций. Преобразования графиков функций" (5-7 минут)
На экране (слайд № 5) вы видите функции. Вам необходимо назвать виды функции и линии, которые являются графиками функций.
у=5
у=а
у=х?+6х+8
у=(х+1)/(х-2)
y = 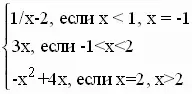
А сейчас три ученика (учитель называет фамилии) строят графики функций (слайд № 6), а класс пишет математический диктант (слайд № 7).
Пусть графически задана функция у=f(х). Я называю преобразование графика, а вам необходимо это преобразование записать с помощью формулы.
1. Сдвиг графика функции y=f(x) по оси ОХ
2. Сдвиг графика функции y=f(x) по оси ОУ
3. Сдвиг графика функции y=f(x) по оси ОХ на а ед. вправо и сдвиг по оси ОУ на b ед. вниз
4. Растяжение по оси ОУ, если b>1; сжатие по оси ОУ , если 0<b<1
5. Отражение графика функции y=f(x) относительно оси ОУ
6. Отражение графика функции y=f(x) относительно оси ОХ
7. Сохранение графика функции y=f(x) для х>0 и отражение этой части графика относительно оси ОУ для х<0
8. Сохранение графика функции y=f(x) для у>0 и отражение графика функции y=f(x) относительно оси ОХ для у<0.
А теперь проверьте правильность выполнения задания.
- y=f(x+a)
- y=f(x)+a
- y=f(x-a)+b, a>0 и b<0
- y=bf(x), b>0
- y=f(-x)
- y=-f(x)
- y=f(|x|)
- y=|f(x) |
(Во время проверки диктанта учитель проверяет правильность построения графиков функций, работает с учениками у доски).
3. Пропедевтика темы 9 класса "Свойства функций" (слайд № 8)
А теперь вспомним свойства функций, которые необходимы при решении уравнений графическим способом (на экране свойства функции, схема)
Опишите по данной схеме свойства квадратичной функции (график функции построен одним из учащихся, работающим около доски).
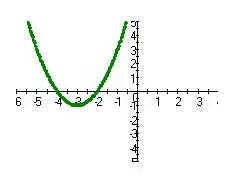
4. Графический способ решения уравнений. (7-10 минут)
А теперь перейдем непосредственно к графическому методу решения уравнений (слайд № 9).
Прочитайте алгоритм решения уравнения графическим способом (на слайде появляются пункты алгоритма).
Задание №1. (слайд № 10)
Решите графически уравнение х?+6х+8=0. (На доске уже построен график функции у=х?+6х+8, а учащиеся строят его у себя в тетрадях).
Вопросы во время работы учащихся с графиком:
- Какая функция соответствует левой части уравнения?
- Какая функция соответствует правой части уравнения?
- Назовите вид функции у=0.
- Что является графиком этой функции? (Показать на доске цветным мелом)
- Сколько корней имеет уравнение? (Показать точки на графике)
- Какие корни? (Записать корни уравнения)
Данное уравнение имеет и другие графические решения (слайды № 11-12). Посмотрим на экран (комментарии слайдов).
Запишем уравнение равносильное данному x?+6x=-8. Рассмотрим функции соответствующие левой и правой частям уравнения.
Вопросы:
- Какая линия является графиком функции y=x?+6x ?
- Какая линия является графиком функции у=-8 ?
- Сколько корней имеет данное уравнение?
- Какие корни?
Какое еще решение квадратного уравнения можно рассмотреть? (Комментарии учителя к решению уравнения x?=-6x-8, слайдам № 13-14)
Задание № 2 Решите графически уравнения:
(х+1)/(х-2)=-2
(х+1)/(х-2)=0
(х+1)/(х-2)=1
(х+1)/(х-2)=2
x?+6x+8 = (х+1)/(х-2)
(Учитель работает со слайдами № 15-18 , а ученики выполняют работу в одной системе координат).
Задание дополнительное (слайд № 19).
Задание № 3 Указать число корней уравнения x?+6x+8 = (х+1)/ (х-2)
Чтобы указать количество корней последнего уравнения (слайды № 20-24 ) необходимо построить графики функций соответствующих частям уравнения в одной системе координат.
Вопрос: Сколько корней имеет данное уравнение?
5. Проверка домашнего задания. (2 минуты)
Вашим домашним заданием было построение графика кусочно заданной функции (слайд № 25)
y = 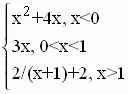
(Комментарии учащихся построения графика, одновременно показ слайдов).
Меня интересуют две точки графика функции с абсциссами х=0 и х=1.
(Комментарии учащихся, одновременно показ слайда № 26).
Если возникли затруднения, то необходимы наводящие вопросы:
- Почему я выделила эти аргументы функции? (Они не входят в область определения функции)
- Как на графике показывают точки? (Выкалывают)
6. Объяснение нового материала (обязательно составить конспект) (15 минут)
Задание (слайд № 27)
- Пусть задана функция y=f(x), где:
f(x) = 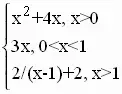
Указать количество корней уравнения
f(x) = а, где а - параметр.
График функции соответствующей левой части уравнения вы построили дома. Все дополнительные построения наносите на чертеж. (Слайды № 28-29)
Вопросы классу.
- Является ли данная функция ограниченной?
- Назовите наименьшее значение функции?
Рассмотрим функцию соответствующую правой части уравнения.
Вопросы.
- Назовите вид функции и линии, которые являются графиками функций у=а.
- Как могут располагаться по отношению к графику функции y=f(x) эти прямые?
- При каком значении параметра а графики функций не пересекаются? (могут назвать конкретные числа, необходимо обобщить и сослаться на свойство ограниченности функции)?
При различных значениях параметра а мы будем получать различное количество точек пересечения графиков функций y=f(x) и у=а. (Рассмотреть по слайду все случаи. Одновременно учащиеся наносят на свои рисунки все графики).
Вопрос классу:
Как определить количество корней уравнения? (По алгоритму решения уравнения графическим способом количество корней уравнения определяется по количеству точек пересечения графиков функций соответствующих левой и правой частям уравнения).
Теперь проведем анализ полученного рисунка и по количеству точек пересечения и ответим на вопрос задачи: сколько корней имеет данное уравнение при различных значениях параметра а?
Ответ: нет корней при a<-4;
один корень при a=-4, a=0, a=3, a>3;
два корня при -4<a<0, 0<a<2, a=2;
три корня при 2<a<3.
Если на уроке останется время, можно провести работу по закреплению графического решения уравнений с параметрами по чертежу, сделанному в начале урока одним из учащихся. Эту работу можно провести в виде самостоятельной работы, в ответ учащиеся записывают только значения параметра а и количество корней.
Задача . На доске график функции
1/х-2, если х<-1,x=-1
у= 3x, если -1<x<2
-х?+4х , если x=2/, x>2
Указать количество корней уравнения
f(x) =а, где а - параметр.
7. Итог урока.
Подведем итог нашего урока, а для этого ответим на вопросы (слайд № 30):
Домашнее задание (слайд № 31)
Заканчиваем урок высказыванием Р.Баха "Иллюзии" (слайд №32)
- Надо же как все просто.
- Как научиться ходить.
Потом ты начинаешь удивляться,
что в этом было такого сложного.
Р.Бах "Иллюзии"
ПРИЛОЖЕНИЯ К УРОКУ
- План-конспект урока представленный выше
- Презентация к уроку Приложение 1
- Практикум к уроку Приложение 2