Изучение темы "Объемы тел" с помощью формулы Симпсона в 11-м классе
Учителя, работающие по учебнику Л.С. Атанасяна, знают порядок вывода формул объемов для изученных в 10-11 классах тел. Знают также и о том, что формулы, начиная уже с формулы для объема наклонной призмы, выводятся с помощью интеграла. А сам интеграл изучается в курсе "Алгебры и начал анализа". Причем в программах (составители Г.М. Кузнецова, Н.Г. Миндюк, Дрофа, 2000) основная цель изучения темы "Интеграл" формулируется так: "познакомить учащихся с интегрированием как операцией, обратной дифференцированию; научить применять первообразную для вычисления площадей криволинейных трапеций". Все! А в геометрии - применяйте определенный интеграл для вывода формул объемов.
Работая в 11 классе, замечал, что учащиеся затрудняются применять интеграл для этих целей, спрашивают, нельзя ли по-другому. Конечно, можно. Один из вариантов - формула Симпсона. (Симпсон Томас (1710-1761) - английский математик)

Как? Приведу возможный порядок изучения теории:
1. Понятие объема. Свойства объемов. (Л.С. Атанасян).
2. Объем прямоугольного параллелепипеда (Л.С. Атанасян).
3. Формула вычисления объемов тел с помощью определенного интеграла (Л.С. Атанасян, но только ввести саму формулу, она пригодится только для следующего пункта).
4. Объем пирамиды.
а) Доказать, что треугольные пирамиды с равновеликими основаниями и равными высотами равновелики (это легко сделать, например, с помощью той самой формулы вычисления объемов тел с помощью определенного интеграла);
б) Формула объема треугольной пирамиды, имеющей три взаимно перпендикулярных ребра, выходящих из одной вершины (вывожу, "дополняя" треугольную пирамиду до прямоугольного параллелепипеда);
в) Формула объема произвольной треугольной пирамиды (опираясь на пункт а);
г) Формула объема произвольной пирамиды (разбиваем произвольную пирамиду на треугольные пирамиды).
5. Призматоид. Формула Симпсона.
Определение призматоида, несложное доказательство самой формулы с иллюстрациями, которые можно увеличить для работы на уроке, исторические сведения приведены, например, в книге И.И. Баврина, В.А. Садчикова "Новые задачи по стереометрии" Москва. Владос. 2000. Там же есть "оговорка" с доказательством на случай, если у учащихся возникнет вопрос, почему эту формулу можно применять, например, к шару. Ведь он - не призматоид. При изучении теории я специально не обратил внимание учащихся на это, применяя формулу Симпсона ко всем телам, но потом было дано задание: найти "слабое место" в этой теории. Такие ученики нашлись. На следующем уроке ими было сказано, что "формула Симпсона - только для призматоидов, а мы ее применили и к цилиндру, и к конусу, и к шару, и к частям шара" Вот здесь и потребовалась та "оговорка", о которой речь шла выше.
6. Вывод формул объемов всех остальных тел с помощью формулы Симпсона, включая объемы частей шара.
К примеру, вывод формулы объема шарового сегмента:

Такое изучение теории высвобождает время для решения задач. Учащиеся с интересом относятся к тому, что одна формула позволяет выводить все остальные, что достаточно запомнить только ее. А уж если забыл какую-нибудь другую, то она легко получается из формулы Симпсона. Кстати, об этой формуле речь идет и в книге Я.И. Перельмана "Занимательная геометрия".
Приведу отрывок из упоминавшейся выше книги И.И. Баврина, В.А. Садчикова "Новые задачи по стереометрии" с доказательством формулы Симпсона для призматоида.
"Призматоид - многогранник, все вершины которого расположены на двух параллельных плоскостях. Грани, расположенные на этих плоскостях, называются основаниями призматоида.
Не будет противоречием определению призматоида, если многогранник, у которого верхнее и нижнее основания являются разноименными многоугольниками, а боковые грани - треугольники, мы будем называть призматоидом.
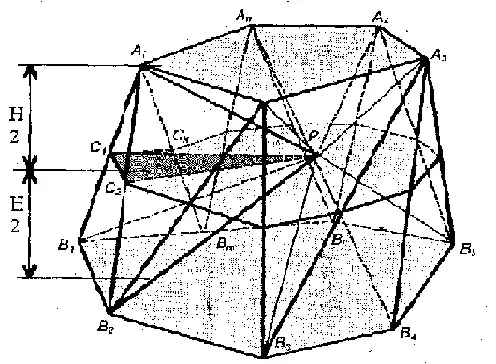
На рисунке многоугольник А1А2А3...Аn- верхнее основание призматоида, площадь этого основания обозначим Sв; многоугольник В1В2В3…Вm - нижнее основание призматоида, площадь этого основания обозначим Sн; многоугольник С1С2С3...Сk - среднее сечение призматоида площадь этого сечения обозначим Sср; высоту призматоида обозначим Н.
Ясно, что плоскость среднего сечения призматоида пересечет боковые ребра в их серединах, то есть граница среднего сечения проходит по средним линиям боковых граней призматоида. Так как плоскость среднего сечения параллельна основаниям призматоида, то эта плоскость проходит и через середину высоты Н призматоида, что нашло отражение на рисунке в виде двух расстояний Н / 2.
Вывод формулы Симпсона. В плоскости среднего сечения С1С2С3...Сk выберем произвольную точку Р. Соединим эту точку со всеми вершинами призматоида. В результате точку Р можно рассматривать как общую вершину совокупности пирамид. Призматоид при этом можно рассматривать как совокупность трех видов пирамид:
1) пирамиды с вершиной Р и основанием А1А2А3...Аn,
2) пирамиды с вершиной Р и основанием В1В2В3…Вm,
3) (к-1) пирамид с вершиной Р и основаниями соответственно треугольники А1В1В2, А1В2А2, А2В2В3,…, А1В1Вm.
Зная, что объем пирамиды вычисляется по формуле V = (1/3)Sh, легко определить объемы каждого из трех видов пирамид, составляющих исходный призматоид:
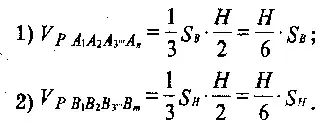
3) Рассмотрим одну из боковых пирамид, например, пирамиду РА1В1В2. Объем этой пирамиды

Аналогично можно представить объемы остальных "боковых" пирамид.
Остается найти сумму объемов всех "боковых" пирамид.

Суммируя объемы совокупности пирамид с вершиной в точке Р, мы находим объем призматоида:
