Основные методы решения задач на смешивание растворов
"Только из союза двоих, работающих вместе и при помощи друг друга, рождаются великие вещи."
Антуан Де Сент-Экзюпери
Математика многообразна и многогранна. Существует ряд ситуаций в образовательном процессе, когда при изучении какой-либо темы по физике, химии, биологии и т.д. затрагиваются понятия математики, например, существуют задачи, которые решают как на уроках математики, так и на уроках химии. Способы решения задач представляют и учителя химии, и математики, но есть проблема: математики знают математику, а химики - химию. И не всегда способы совпадают.
В данной статье приводятся рекомендации по решению химических задач на смешение растворов разными способами: с помощью расчетной формулы, "Правила смешения", "Правила креста", графического метода, алгебраического метода. Приведены примеры решения задач.
1. Основные химические понятия
Приведем некоторые указания к решению задач на растворы.
Основными компонентами этого типа задач являются:
а) массовая доля растворенного вещества в растворе;
б) масса растворенного вещества в растворе;
в) масса раствора.
Предполагают, что:
а) все получившиеся смеси и сплавы являются однородными;
б) смешивание различных растворов происходит мгновенно;
в) объем смеси равен сумме объемов смешиваемых растворов;
г) объемы растворов и массы сплавов не могут быть отрицательными.
Определения и обозначения.
Массовая доля растворенного вещества в растворе - это отношение массы этого вещества к массе раствора.
![]()
где ![]() - массовая доля растворенного вещества в растворе;
- массовая доля растворенного вещества в растворе;
![]() - масса растворенного вещества в растворе;
- масса растворенного вещества в растворе;
![]() - масса раствора.
- масса раствора.
Следствия формулы (1):
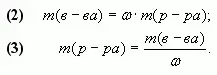
Введем обозначения:
![]() - массовая доля растворенного вещества в первом растворе;
- массовая доля растворенного вещества в первом растворе;
![]() - массовая доля растворенного вещества во втором растворе;
- массовая доля растворенного вещества во втором растворе;
![]() - массовая доля растворенного вещества в новом растворе, полученном при смешивании первого и второго растворов;
- массовая доля растворенного вещества в новом растворе, полученном при смешивании первого и второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) - массы растворенных веществ в соответствующих растворах;
m1(р-ра), m2(р-ра), m(р-ра) - массы соответствующих растворов.
Основными методами решения задач на смешивание растворов являются: с помощью расчетной формулы, "Правило смешения", "Правило креста", графический метод, алгебраический метод.
Приведем описание указанных методов.
1.1. С помощью расчетной формулы
В наших обозначениях, получим формулу для вычисления массовой доли вещества (?) в смеси.
1. Масса полученного при смешивании раствора равна:
m(р-ра) = m1(р-ра) + m2(р-ра).
2. Определим массы растворенных веществ в первом и втором растворах:
m1(в-ва)= ![]() •m1(р-ра), m2(в-ва)=
•m1(р-ра), m2(в-ва)= ![]() •m2(р-ра).
•m2(р-ра).
3. Следовательно, масса растворенного вещества в полученном растворе вычисляется как сумма масс веществ в исходных растворах:
m(в-ва) = m1(в-ва) + m2(в-ва) = ![]() •m1(р-ра) +
•m1(р-ра) + ![]() •m2(р-ра).
•m2(р-ра).
4. Таким образом, массовая доля растворенного вещества в полученном растворе равна:
![]()
или
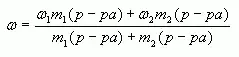
или
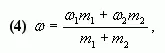
где ![]() - массы соответствующих растворов.
- массы соответствующих растворов.
Замечание: При решении задач удобно составлять следующую таблицу.
|
1-й раствор |
2-й раствор |
Смесь двух растворов |
|
|
Масса растворов |
m1 |
m2 |
m1 + m2 |
|
Массовая доля растворенного вещества |
|
|
|
|
Масса вещества в растворе |
|
|
|
1.2. "Правило смешения"
Воспользуемся формулой (4): ![]()
тогда 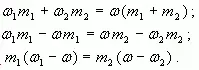
Отсюда ![]()
Таким образом, отношение массы первого раствора к массе второго равно отношению разности массовых долей смеси и второго раствора к разности массовых долей первого раствора и смеси.
Аналогично получаем, что при ![]()
Замечание: Формула (5) удобна тем, что на практике, как правило, массы веществ не отвешиваются, а берутся в определенном отношении.
1.3. "Правило креста"
"Правилом креста" называют диагональную схему правила смешения для случаев с двумя растворами.
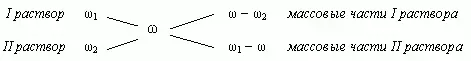
Слева на концах отрезков записывают исходные массовые доли растворов (обычно слева вверху-большая), на пересечении отрезков - заданная, а справа на их концах записываются разности между исходными и заданной массовыми долями. Получаемые массовые части показывают в каком отношении надо слить исходные растворы.
1.4. Графический метод
Отрезок прямой (основание графика) представляет собой массу смеси, а на осях ординат откладывают точки, соответствующие массовым долям растворенного вещества в исходных растворах. Соединив прямой
точки на осях ординат, получают прямую, которая отображает функциональную зависимость массовой доли растворенного вещества в смеси от массы смешанных растворов в обратной пропорциональной зависимости
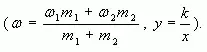
Полученная функциональная прямая позволяет решать задачи по определению массы смешанных растворов и обратные, по массе смешанных растворов находить массовую долю полученной смеси.
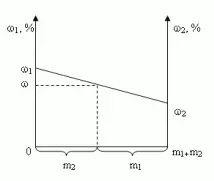
Построим график зависимости массовой доли растворенного вещества от массы смешанных растворов. На одной из осей ординат откладывают точку, соответствующую массовой доли ![]() , а на другой -
, а на другой - ![]() . Обозначим на оси абсцисс точки А и В с координатами (0,0)
и (m1 + m2,0), соответственно. На графике точка А(0,0) показывает, что массовая доля всего раствора равна
. Обозначим на оси абсцисс точки А и В с координатами (0,0)
и (m1 + m2,0), соответственно. На графике точка А(0,0) показывает, что массовая доля всего раствора равна ![]() , а точка В(m1 + m2,0) - массовая доля всего раствора равна
, а точка В(m1 + m2,0) - массовая доля всего раствора равна ![]() . В направлении от точки
А к точке В возрастает содержание в смеси 2-го раствора от 0 до m1+ m2 и убывает содержание 1-го раствора от m1+ m2 до 0.
Таким образом, любая точка на отрезке АВ будет представлять собой смесь, имеющую одну и ту же массу с определенным содержанием каждого раствора, которое влияет на массовую долю
растворенного вещества в смеси.
. В направлении от точки
А к точке В возрастает содержание в смеси 2-го раствора от 0 до m1+ m2 и убывает содержание 1-го раствора от m1+ m2 до 0.
Таким образом, любая точка на отрезке АВ будет представлять собой смесь, имеющую одну и ту же массу с определенным содержанием каждого раствора, которое влияет на массовую долю
растворенного вещества в смеси.
Замечание: Данный способ является наглядным и дает приближенное решение. При использовании миллиметровой бумаги можно получить достаточно точный ответ.
1.5. Алгебраический метод
Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений.
2. Примеры решения задач
Задача 1. (№1.43, [1])
В 100 г 20%-ного раствора соли добавили 300 г её 10%-ного раствора. Определите процентную концентрацию раствора.
Решение:
-
C помощью расчетной формулы

-
Графический
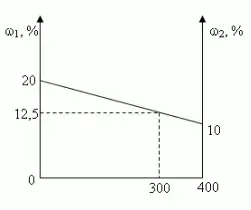
Ответ: 12,5%
-
Путем последовательных вычислений
- Сколько растворенного вещества содержится:
-
а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]
б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]
- Сколько вещества содержится в образовавшемся растворе?
-
20 г + 30 г = 50 г
- Чему равна масса образовавшегося раствора?
-
100 г + 300 г = 400 г
- Какова процентная концентрация полученного раствора?
-
(50/400)100 = 12,5(%)
Ответ: 12,5%
-
Алгебраический
Пусть х - процентная концентрация полученного раствора. В первом растворе содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в полученном растворе х•(100 + 300)(г) соли. Составим уравнение:
0,2•100 + 0,1•300 = х•(100 + 300);
х = 0,125 (12,5%)
Ответ: 12,5%
Задача 2. u(№10.26, [1])
Смешали 10%-ный и 25%-ный растворы соли и получили 3 кг 20%-ного раствора. Какое количество каждого раствора в килограммах было использовано?
Решение:
-
Алгебраический
а) C помощью уравнения:
Пусть х (кг) - масса 1-го раствора, тогда 3-х (кг) -масса 2-го раствора.
0,1•х (кг) содержится соли в 1-ом растворе,
0,25•(3-х) (кг) содержится соли в 2-ом растворе,
0,2•3 (кг) содержится соли в смеси.
Учитывая, что масса соли в 1-ом и 2-ом растворах равна массе соли в смеси, составим и решим уравнение:
0,1•х + 0,25•(3-х) = 0,2•3;
0,15х = 0,15;
х = 1, 1кг-масса 1-го раствора
3 - х = 3 - 1 =2 (кг) - масса 2-го раствора.
Ответ: 1 кг, 2 кг.
б) С помощью системы уравнений
Пусть х (кг) - количество первого раствора, у (кг) - количество второго раствора. Система уравнений имеет вид:
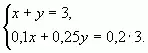
Ответ: 1 кг, 2 кг.
-
Графический.
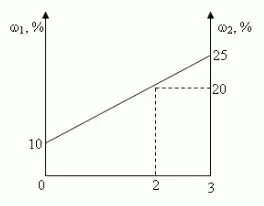
Ответ: 1кг, 2кг.
-
"Правило смешения"

-
"Правило креста"
Составим диагональную схему
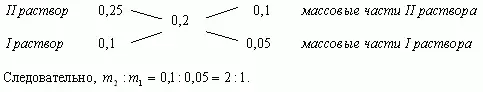
Ответ: 1кг, 2кг.
Задача 3 ([2])
Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму) раствора соли. Сколько литров 20%-ного раствора такой же соли надо налить в сосуд, чтобы процентное содержание соли в сосуде стало наибольшим?
Решение (графический способ)

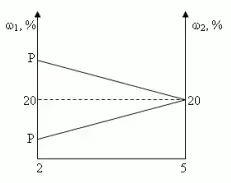
Заметим, что по условию, объём второго раствора не превышает трёх литров.
- Ели р < 20, то для того, чтобы получить максимальную массовую долю вещества в растворе, необходимо добавить 3 л 20% - ного раствора соли;
- Если р = 20, то при добавлении 2-го раствора, процентное содержание соли в растворе не изменится, следовательно, можно прилить от 0 л до 3 л 20% - ного раствора соли;
- Если р > 20, то при добавлении 2-го раствора, процентное содержание соли будет уменьшаться, т.е. прилить нужно 0 л.
Ответ: 3 л, если 0 < р < 20, [0,3], если р = 20, 0л, если 20 < р ![]() 100.
100.
Задача 4 (работа 5, №2, [1])
В двух сосудах по 5л каждый содержится раствор соли. Первый сосуд содержит 3л р% - ного раствора, а второй - 4л 2р% - ного раствора одной и той же соли. Сколько литров надо перелить из второго сосуда в первый, чтобы получить в нем 10% - ный раствор соли? При каких значениях р задача имеет решение?
Решение

Найдем, при каких значениях р задача имеет решение. По условию задачи 5-ти литровый сосуд содержит 3л первого раствора, следовательно, к нему можно прилить от 0 до 2л второго раствора.
Имеем, ![]() Решая неравенство, получаем
Решая неравенство, получаем ![]()
Ответ: ![]()
3. Заключение
Данные рекомендации предназначены учителям математики, желающим организовать элективные курсы, как в девятых, так и в десятых и одиннадцатых классах. Цель создаваемых курсов: научить учащихся пользоваться математическим аппаратом при решении химических задач.
Список литературы
- Галицкий и др. Сборник задач по алгебре для 8-9 классов: Учебное пособие для учащихся шк. и классов с углубл. изуч. математики / М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич.-2-е изд. - М.: Просвещение,1994. - 271с.
- Сборник задач по математике для поступающих в вузы: Учебное пособие/ П.Т.Дыбов, А.И.Забоев, А.С. Иванов и др.; Под ред. А.И. Прилепко. - М.:Высш. школа, 1983. - 239 с.
- Ерыгин Д.П., Шишкин Е.А. Методика решения задач по химии: Учебное пособие для студентов пед. ин-тов по биол. и хим. спец. - М.: Просвещение,1989. - 176с.
- Хомченко Г.П., Хомченко И.Г. Задачи по химии для поступающих в вузы: Учебное пособие. - 2-е изд.. исправ. и доп. - М.: Высш. школа, 1993. - 302 с.