Об электронном проектировании арифметических упражнений
В настоящей статье автор даёт заметки из опыта своей работы в школе и пединституте, приводит примеры компьютерного проектирования индивидуальных заданий для тренировочных упражнений и контрольных работ по школьной математике и алгебраическим дисциплинам пединститута. Приведенные примеры будут полезны учителю математики, который использует возможности Microsoft Excel.
Применение электронного проектирования заданий и их использование рассмотрим в двух системах: А = {S-P-M} и Б = {S-P-M-S}. S - студент (ученик), P - педагог (учитель математики), M - ЭВМ. В первой системе компьютер остаётся за кулисами, в звене P-M готовятся задания, в звене P-S проходит обучение без участия ЭВМ. Здесь представлена система А. С этим связана нумерация примеров.
А1. Арифметические примеры с целыми числами.
С помощью электронной таблицы Excel составляется система арифметических упражнений для повторения порядка действий, вычисления неизвестных компонентов, навыков операций с многозначными числами. Формула (a* b+ c)/ d- e* f+ g=h представлена таблицей 1, реализована по следующему алгоритму:
- d=40+ОКРУГЛ(СЛЧИС()*50;0), т.е. выбирается случайное число из интервала d
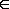 (40,90); d
записывается в столбце D;
(40,90); d
записывается в столбце D; - e = ОКРУГЛВНИЗ(3000/d;0), e
 столбец E;
столбец E; - a = 40+ОКРУГЛ(СЛЧИС()*50;0); a
 столбец A;
столбец A; - b = d *ОКРУГЛВНИЗ(1+СЛЧИС()*6;0);
- a*b
 столбец C;
столбец C; - ( ) =C+ОКРУГЛ(СЛЧИС()*A;0)*D; ( )
 столбец F;
столбец F; - c= F - A*B = |()-ab|; c
 столбец G;
столбец G; - H = (A*B+C)/D;
 столбец H;
столбец H; - e = 40+ОКРУГЛ(СЛЧИС()*50;0); e
 столбец I;
столбец I; - f = ОКРУГЛВНИЗ(40+СЛЧИС()*50;0); f
 столбец J;
столбец J; - g = (800+ОКРУГЛ(СЛЧИС()*1200;0)); g
 столбец K;
столбец K; - h =I*J - H+K;
 столбец L.
столбец L.
Большими буквами обозначены столбцы, курсивом - буквы формулы.
В таблице 1 отражены строки листа Excel. В первой строке - имена столбцов, во второй - формула-заготовка для задания, в третьей - параметры, далее их значения. Закрашенные столбцы закрываются. Кроме того, перед выдачей задания одно какое-либо число скрывается (заменяется буквой). Задание: найти неизвестное число как компонент действия с натуральными числами.
Таблица 1
| A | B | C | D | E | F | G | H | I | J | K | L |
| (a*b+c)/d-e*f+g=h | |||||||||||
| a | b | a* b | d |
целое
(15000/ d) |
() | c | g3/d3 | e | f | g | h |
| 42 | 252 | 10584 | 42 | 71 | 12222 | 1638 | 504 | 46 | 84 | 1943 | 5303 |
| 88 | 162 | 14256 | 54 | 55 | 14310 | 54 | 528 | 78 | 69 | 885 | 5739 |
| 60 | 46 | 2760 | 46 | 65 | 3634 | 874 | 120 | 64 | 57 | 1756 | 5284 |
| 72 | 336 | 24192 | 84 | 35 | 24360 | 168 | 576 | 45 | 76 | 1692 | 4536 |
| 58 | 82 | 4756 | 82 | 36 | 8692 | 3936 | 116 | 43 | 81 | 1450 | 4817 |
| 65 | 174 | 11310 | 58 | 51 | 14848 | 3538 | 390 | 65 | 89 | 893 | 6288 |
| 77 | 73 | 5621 | 73 | 41 | 10366 | 4745 | 154 | 81 | 76 | 1937 | 7939 |
Формула позволяет составить 8 видов заданий по числу букв: задание "a" - закрыта буква "a", …, задание "g" - закрыта буква "g". На листе напечатано столько примеров, сколько учеников. Нажав клавишу "F9", мгновенно изменяем все значения таблицы. Только перед нажатием печатаем вторую страницу - для учителя.
Размеры числовых интервалов зависят от цели, какую преследует учитель: малые - для усвоения учениками порядка действий, для демонстрации нахождения неизвестных компонентов, большие - для закрепления навыков арифметических действий с многозначными числами.
Аналогичные формулы применимы для закрепления навыков операций с десятичными дробями.
А2. Системы счисления.
Для развития навыков вычислений с систематическими числами в различных системах счисления составляются виды (формулы)
Ao1 y Bo2 y Ro3 y Co4 y Do5 = Eo6
Здесь A , B , Ro3 , Co4 , Do5 , Eo6 - числа, индексы o1, o2, …- основания систем счисления (ОСС), символ y - какие-то операции. Примеры:
№ 1. 34136 * 44515 - R6* 47513 + B213 = 13230711;
№ 2. 21357 * R14 - 103215 * 13313 + 114105 = CA7213;
№ 3. 8309 * R14 + 23615 - 7358 * 27012 = 12B2B012;
№ 4. 15214 + 10778 * R14 - 3557 * 15B13 = 164A6612;
№ 5. 6047 * R11 + 4249 - 4556 * 46815 = 5227A11.
С конкретными примерами даётся следующее задание:
Перевести все числа в ту СС, которая указана для неизвестного числа R, и в этой СС выполнить указанные операции для нахождения R, как неизвестного компонента действий.
Чтобы задания были корректны, подготовительная работа выполняется в следующем порядке:
- составляются арифметические примеры в десятичной СС; например:
801 * 965 - 732 * 772 + 145 = 208006; - производится распечатка для учителя;
- каждое число переводится в какую-либо СС, причем для всех чисел разные ОСС, чтобы при переводе приходилось менять ОСС как на увеличение, так и на уменьшение;
- переводятся все числа в СС, указанную для R;
- производится распечатка для учителя;
- закрывается число согласно заданному виду;
- производится распечатка для студента.
Для каждого студента готовились два варианта задания: первый - числа не превышали 1000 в десятичной СС, второй - числа - пяти-шестизначные.
А3. Делимость целых чисел.
Для закрепления знаний свойств и признаков делимости даются задания вида: найти цифры u, v в числах столбца G (или H, I, J), которые делятся соответственно на числа столбца D. Ученику не показывается столбец C (один из ответов, для учителя).
Таблица 2
| C | D | G | H | I | J | |
| B2*D2 | зам(с2;4;1;'u') | замE3;7;1;v | замE3;8;1;v | замF3;8;1;v | ||
| 1 | 1556334 | 6 | 155u3v4 | 378u23v | 155u334v | 1556u34v |
| 2 | 3787230 | 15 | 378u2v0 | 378u23v | 378u230v | 3787u30v |
| 3 | 30197196 | 18 | 301u7v96 | 301u71v6 | 301u719v | 3019u19v |
| 4 | 71493768 | 24 | 714u3v68 | 714u37v8 | 714u376v | 7149u76v |
| 5 | 104636448 | 36 | 104u3v448 | 104u36v48 | 104u364v8 | 1046u64v8 |
| 6 | 108198728 | 44 | 108u9v728 | 108u98v28 | 108u987v8 | 1081u87v8 |
| 7 | 180430848 | 72 | 180u3v848 | 180u30v48 | 180u308v8 | 1804u08v8 |
| 8 | 249629925 | 75 | 249u2v925 | 249u29v25 | 249u299v5 | 2496u99v5 |
Для иллюстрации здесь выбраны 8 значений. Эти и другие подобные задания проектируются от ответов. В таких случаях обязательно находится решение, хотя бы методом полной индукции. Но можно изменить задание на невыполнимость операции, например, одно и то же число с неизвестными двумя цифрами делится на разные делители.
Случайные числа из выбранного интервала умножаются на выбранный делитель. Возможен следующий алгоритм проектирования, вторая строчка показывает реализацию алгоритма:
- выбор d из D, D1, D2.
D = {6, 12, 15, 18, 22, 24, 33, 36, 44, 72, 75}
D1 = {4, 8, 9, 11, 25, 30, 40, 45, 66}
D2 = {7, 14, 21, 28, 35, 42, 56, 63, 77, 91, 98} - выбор ограничений B, A;
- M = B + ОКРУГЛ(СЛЧИС()* (A-B);0);
- C = D* M.
Другой вариант на распознавание цифр. Даны числа A, B. В каждом числе по одной закрытой цифре. Узнать эти цифры, если A делится на B. Такая задача составляется от ответа.
А4. Делители, кратные, разложение на множители.
Задание 1. Даны A, B, C - шестизначные числа. Найти их наибольший общий делитель и наименьшее общее кратное:
- по алгоритму Евклида;
- по разложению на простые множители.
Задание 2. Сократить дробь P/Q, где P и Q - шестизначные числа.
Таблица 3
| A | B | C | P | Q |
| 526552 | 220116 | 852410 | 358938 | 534888 |
| 501492 | 214406 | 506943 | 323190 | 488376 |
| 464280 | 290175 | 773800 | 293040 | 455840 |
Для таких задач мы создаём различные массивы из простых чисел определённой длины, например, массив из всех двузначных простых чисел и массив из трёхзначных простых чисел, которые парами входят в каноническое разложение данных чисел.
А5. Обращение дробей.
Пример. Обратить периодические десятичные дроби в обыкновенные несократимые:
Студенты испытывают затруднения при сокращении, если числитель и знаменатель - многозначные числа. Поэтому имеет смысл заранее подобрать числитель и знаменатель искомых дробей. Пусть дана периодическая десятичная дробь a = 0.As(Pk) с длиной предпериода s и длиной периода k. Тогда а = (A* 10k-A+ P)/10s/(10k-1) или
A = [A* (10k-1)+P]/10s/(10k-1).
Сокращение на 2 и 5 не вызывает затруднений. Следовательно, необходимо разложение разности 10k-1, т.е. числа из девяток. В таблице 4 приведены все знаменатели (до 2000) дробей 1/b, которые обращаются в чисто периодические с длиной периода k.
Таблица 4
| Знаменатели несократимых дробей b | Длина периода k |
| 3, 9 | 1 |
| 11, 33, 99 | 2 |
| 27, 37, 111, 333, 999 | 3 |
| 101, 303, 909, 1111 | 4 |
| 41, 123, 271, 369, 813 | 5 |
| 13, 21, 39, 63, 77, 91, 117, 143, 189, 231,259, 273, 297, 351, 407, 429, 481, 693, 777, 819, 1001, 1221, 1287, 1443 | 6 |
| 239, 717 | 7 |
| 73, 137, 219, 411, 657, 803, 1233, 1507 | 8 |
| 81 | 9 |
| 451, 1353 | 10 |
А6. Приближенные вычисления.
Распространение калькуляторов и персональных компьютеров не могут автоматически поддерживать вычислительную культуру пользователей. Требуются усилия для достижения вычислительной грамотности и воспитания вычислительной культуры. Использование и обработка результатов измерений, оформление вычислительной работы требуют аккуратности. Практически в школьных тетрадях и в студенческих отчетах часто встречаются безответственные вычисления (например, выдача числовых ответов со всеми десятичными знаками, какие выдаёт компьютер, вместо трех достаточных; нарушение соразмерности различных величин, как длин сторон и угловых значений).
ЭВМ не владеет культурой приближённых вычислений.
Важное значение имеют лабораторные работы по приближенным вычислениям и измерительные работы на местности с последующей обработкой результатов. На первых занятиях студенты допускали погрешности не только систематические, но и грубые, превышающие результаты. В школе обязательны знания и навыки операций с округленными числами. Кроме этого, от студентов требуем знаний по исследованию погрешностей, вычислению методом границ, применению приближенных формул, по интерполяции и экстраполяции. Приведем пример вычислительного задания.
- Числа A, B - округлённые. Требуется вычислить: S= A+B, R= A-B, P= A* B, Q= A/ B, T= B/ A, O= 1/A, Kb= A2, Ko= sqr(A), L= log(A), E= exp(A), E2= exp(B), A^B, B^A.
- Те же числа A, B, но даны с относительной погрешностью в 1%. Вычислить S, R, P, Q, T. Указать абсолютную погрешность результатов с одной значащей цифрой.
- Даны относительные погрешности d (A) и d (B). Вычислить их абсолютные погрешности. Вычислить S, R, P, Q, T. Ответы дать с указанием абсолютных погрешностей.
Таблица 5
| Задания | 1 | 2 | 3 | |
| Числа | округлённые | Относ. погреш. | Относ. погреш. | |
| A | 32.60067 | 1% | 1,30% | |
| B | 4.27. | 1% | 0,70% | |
| Ответы | ||||
| S | a+b | 36.87 | 36.9±0.4 | 36.8±0.5 |
| R | a-b | 28.33 | 28.3±0.4 | 28.3±0.5 |
| P | a* b | 139.14 | 139±3 | 139±3 |
| Q | a/b | 7.64 | 7.6±0.2 | 7.6±2 |
| T | b/a | 0.131 | 0.131±0.003 | 131±0.003 |
| O | 1/a | 0.0009412 | ||
| Kb | a* a | 1062.804 | 1060±30 | |
| Ko | кв.корень | 5.7097 | 5.71±0.04 |
Студентам таблица представлялась образцом по оформлению, но не по ответам. Отчет показывал грамотность вычислений студента и культуру оформления ответов. Как правило, затруднения вызывали задания вида: вычислить log(A), exp(A), exp(B), AB , BA .
А7. Квадратные уравнения.
Проектировать упражнения и контрольные задания нетрудно, от учителя требуется разнообразие вариантов по заданиям и ответам. Мы исходим из получаемых ответов и разбросу порядка представления заданий. Сами задания проектируются от вида ответов, от которых зависит и нумерация, а коэффициенты от Randomize и интервалов для коэффициентов. В таблице 6 представлены виды уравнений с целыми коэффициентами. Номера примеров заменяются на порядок 1-10.
Таблица 6
| Решить уравнения:Ax2 +Bx +C =0 | ||||||||
| № | A | B | C | № | A | B | C | |
| 10 | 2 | -14 | -1 | 3 | 48 | -38 | -21 | |
| 2 | 1 | 16 | 64 | 6 | 4 | 0 | -5 | |
| 8 | 3 | -2 | 7 | 4 | 9 | 42 | 49 | |
| 1 | 1 | -11 | 28 | 9 | 7 | -19 | -8 | |
| 7 | 6 | -5 | -11 | 5 | 25 | 0 | -1 | |