Алгоритмы обработки одномерных массивов

В современной школе информатика – достаточно сложный предмет для усвоения учащимися. Основное препятствие для полноценного изучения информатики – нехватка времени. Мною проанализировано много учебных планов и методик преподавания информатики и для общеобразовательных классов, и для профильных с углубленным изучением информатики. Вывод неутешителен. Предлагаемые материалы основываются на гораздо большем годовом количестве учебных часов, чем то, которым мы реально располагаем. Следствием расхождения между рекомендуемым и реальным объемом учебных часов является невозможность использовать в процессе обучения какой-то один учебник информатики. Это неудобно как ученикам, так и преподавателю. Выходом из этой ситуации является разработка собственной методики преподавания информатики с ориентацией на творческую деятельность учащихся и тестовый контроль, которая, не уменьшая объем материала, позволяла бы сократить время на его усвоение учениками и уложиться в отведенное количество часов.

Основываясь на своем опыте работы с учащимися старшего звена, я выделила несколько основных тем, без усвоения которых невозможно успешное изучение всего курса информатики, и разработала собственную методику их преподавания. Я пользуюсь ей уже несколько лет, что позволяет добиваться хороших результатов в освоении учениками моего предмета. С методикой преподавания одной из таких тем я и хочу познакомить вас.

Секрет могущества ЭВМ – высокая скорость и большая память. Для записи алгоритмов, работающих с большими объемами информации, в алгоритмическом языке существуют специальные табличные величины (или просто таблицы). Исполнение многих алгоритмов было бы просто невозможно, если бы соответствующие объекты не были каким-либо образом организованы: упорядочены, классифицированы, занумерованы и так далее. Итак, нужно уметь организовать не только действия, но и те объекты, над которыми эти действия производятся.

Необходимо отметить, что таблицы (массивы) как основное средство представления однородной информации неизбежно используются во всех реальных компьютерных программах. На табличном принципе основана и архитектура современных ЭВМ: память машины можно рассматривать как большой массив байтов, адреса которых располагаются по возрастанию.

Следовательно, без понимания информационной сущности таблиц и основных алгоритмов их обработки невозможно формирование полноценных представлений о возможностях ЭВМ и принципах их работы. Для построения сколь-нибудь сложных и содержательных программ необходимо уверенное владение общими принципами применения таблиц и базовыми приемами их обработки. В данной работе будет рассмотрен ряд простых алгоритмов, которые используются при построении более сложных.

Алгоритм вычисления суммы

1. Пусть дан массив A, состоящий из n элементов: a₁, a₂, a₃, …, a_n. Нужно найти их сумму, т.е. S=a₁+a₂+a₃+…+a_n.

Нахождение суммы есть последовательное нахождение суммы по формулам:

S=0 S=S+a₂ … S=S+a_i S=S+a_n

S=S+a₁ S=S+a₃ …

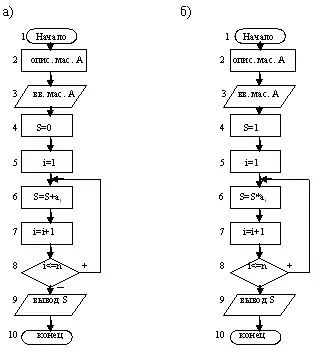
Алгоритм вычисления суммы удобно организовать циклом, взяв за параметр цикла переменную i, которая меняется от 1 до n с шагом 1, и записав в цикле формулу S=S+a_i один раз. Схема алгоритма приведена на рис. 1а.

В схеме блок 4 присваивает S нулевое значение, блок 5 счетчику i присваивает начальное значение, блок 6 выполняет накопление суммы, блок 7 изменяет значение i на 1, блок 8 осуществляет проверку условия повторения цикла. При выполнении этого условия управление передается в начало цикла, а при невыполнении – осуществляется выход из цикла, т.к. при i=n+1 суммировать не нужно. n – в схеме предполагается число, но n может быть и переменной, значение которой равно числу элементов массива A, которое нужно вводить перед описанием массива.

При разработке этого алгоритма учащимся можно предложить изменить схему на случай, если нужно найти сумму элементов, расположенных на четных местах в массиве A (Ответ: Блок 5 надо изменить на i=2 и блок 7 на i=i+2) или задать вопрос – что изменится в схеме на рис.1а, если суммировать только положительные элементы массива A? (Ответ: Перед блоком суммирования 6 нужно поставить блок проверки элемента массива a_i на положительность и, если он положителен, то его суммировать, а если нет, то обходить блок суммирования.) Схема алгоритма будет иметь вид:

При таком тщательном исследовании схемы алгоритма учащиеся без особых затруднений ответят на вопрос – что добавить в схеме на рис.2, чтобы в ней подсчитывалось еще количество положительных элементов массива?

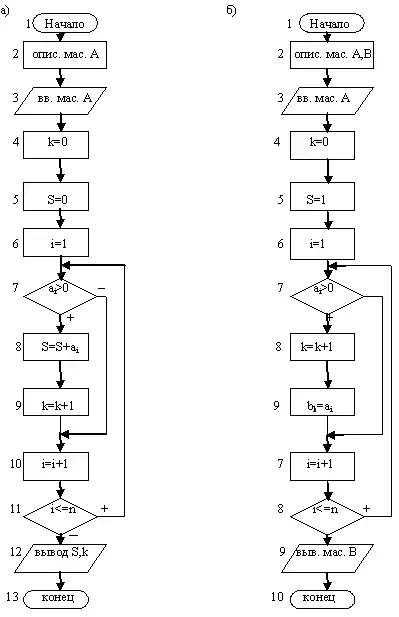
(Ответ: Надо ввести переменную k для получения количества положительных элементов и перед циклом присвоить ей значение 0. После блока проверки 7 по пути “+” нужно поставить блок, содержащий k=k+1, который ведет счет количества положительных элементов массива A.) Схема алгоритма приведена на рис.3а.

Алгоритм вычисления произведения

Этот алгоритм предлагается учащимся разработать самостоятельно, взяв за основу алгоритм определения суммы элементов массива (Рис. 1а). Учащиеся должны не только указать на изменения блока 6 на S=S*a_i (в S будет направляться произведение элементов), но и дать четкое объяснение изменению блока 4 на S=1. Схема алгоритма представлена на рис.1б.

Алгоритм формирования нового массива

Как положительные элементы массива A сформировать в массив? Обозначим массив положительных элементов B и по пути “+” после блока 7 поставим присвоение соответствующему элементу массива B элемент массива A, т.е. блок, содержимое которого b_k=a_i.

k будем использовать как меняющийся индекс нового массива. Необходимо обратить внимание учащихся на блок 2, в котором требуется описать массив B, указав количество его элементов равное количеству элементов массива A. Схема алгоритма на рис.3б.

Алгоритм определения максимального элемента

Для получения максимального числа введем переменную M и ей присвоим значение первого элемента массива a₁, а затем необходимо сравнить M с текущим элементом массива a_i и если текущий элемент будет больше M, то значение M заменить на значение этого элемента. Схема алгоритма на Рис. 4. Очень важно обратить внимание учащихся на начальное значение переменной M. Почему, например нельзя переменной M присвоить значение равное нулю? (Ответ: Для массива с отрицательными значениями элементов максимум не будет найден.)

Алгоритм упорядочения массива методом “Пузырька”

Действия по упорядочению некоторых данных по ключу называются процессом сортировки. Очевидно, что с отсортированными данными работать легче и быстрее, чем с произвольно расположенными. Все применения ЭВМ основаны на их способности к быстрой и точной обработке больших объемов информации, а это возможно только тогда, когда информация однородна и отсортирована. Существует довольно много различных методов сортировки, отличающихся друг от друга степенью эффективности, под которой понимается количество сравнений и количество обменов, произведенных в процессе сортировки, время выполнения и объем занимаемой ОП. Рассмотрим сортировку методом “Пузырька”, которая легко описывается в форме четких алгоритмов и приводит к простой программной реализации.

Одномерный массив A из n элементов упорядочим по возрастанию. При пузырьковой сортировке элементы массива попарно сравниваются и более “легкие” элементы как бы всплывают на поверхность. При реализации алгоритма возникает проблема в определении количества шагов сортировки. Для решения этой задачи воспользуемся известным методом “расстановки флажков”, благодаря которому однозначно будет определен момент завершения сортировки и выхода из цикла (блок 5).

В качестве “флажка” возьмем числовую переменную F и присвоим ей произвольное начальное значение отличное от нуля (блок 4). Схема алгоритма на рис. 5. По парное сравнивание элементов и их обмен местами происходит в блоках 9-12, здесь же изменяется значение флажка (блок 13). В случае, когда все элементы массива будут упорядочены, значение F останется равным нулю (блок 6). Блоки 3 и 15 являются укрупненными, т.к. алгоритмы ввода и вывода элементов массива подробно не описаны на схеме (Рис. 5).

В помощь учащимся общеобразовательной школы мною разработано методическое пособие по алгоритмам обработки массивов данных, в котором подробно рассматриваются элементарные алгоритмы, используемые при составлении более сложных алгоритмов, и прилагается большая подборка задач.

Задачи “Первые шаги”

1. В массиве а₁, а₂, ..., а₅₀ определить количество нулей.
2. В массиве d₁, d₂, …, d₃₅ найти сумму чисел, расположенных на нечетных местах.
3. В массиве с₁, с₂ , ..., с₄₀ найти произведение отрицательных чисел.
4. В массиве b₁, b₂, ..., b₄₅ найти сумму отрицательных чисел.
5. В массиве b₁, b₂, ..., b₂₀ найдите количество "единиц".
6. Из массива а₁, а₂ , ..., а₃₀ найти произведение чисел, расположенных на нечетных местах.
7. В массиве с₁, с₂ , ..., с₄₀ найти сумму чисел больших единицы.
8. В массиве чисел а₁, а₂ , ..., а₅₀ найти количество чисел меньших единицы.
9. В массиве с₁, с₂ , ..., с₃₇ найти произведение чисел больших 2.
10. В массиве а₁, а₂ , ..., а₄₀ найти сумму чисел, расположенных на местах кратных 3.
11. В массиве а₁, а₂ , ..., а₅₀ найти произведение чисел меньших или равных 2.
12. В массиве b₁, b₂, ..., b₄₅ найти количество чисел равных 3,5.
13. В массиве d₁, d₂, ..., d₅₀ найти сумму чисел равных 4,7.
14. В массиве b₁, b₂, ..., b₃₀ найти произведение чисел больших или равных 5.
15. В массиве с₁, с₂ , ..., с₇₀ найти количество "нулей", стоящих на нечетных местах.
16. В массиве b₁, b₂, ..., b₆₅ найти сумму чисел больших или равных 5.
17. В массиве d₁, d₂, …, d₃₀ найти произведение чисел, исключая первый и последний элемент.
18. В массиве а₁, а₂ , ..., а₃₅ найти количество "единиц", стоящих на четных местах.
19. В массиве чисел а₁, а₂ , ..., а₃₀ найти сумму отрицательных чисел, стоящих на нечетных местах.
20. В массиве чисел в₁, в₂, ..., в₃₅ найти произведение чисел больших или равных 2.
21. В массиве чисел с₁, с₂, …, с₄₀ найти количество чисел, попавших в интервал [а, в]
22. В массиве чисел с₁, с₂, …, с₄₀ найти сумму чисел, не попавших в интервал [с, d].
23. В массиве чисел в₁, в₂, ..., в₄₅ найти произведение всех ненулевых чисел.
24. В массиве чисел с₁, с₂, ..., с₆₀ найти количество нулей стоящих на местах, кратных 4 т.е. среди чисел с₄, с₈, ..., с₆₀.
25. В массиве чисел z₁, z₂, ..., z₂₀₀ найти сумму чисел z₅, z₁₀, ..., z₂₀₀.

Задачи “Джентльменский набор”.

1. Даны три последовательности чисел а₁, а₂, ..., a₉, b₁, b₂ ..., b₉, с₁, с₂, ..., с₉. Составьте новую последовательность d₁, d₂, …, d₉, каждый элемент которой определяется по правилу d_i = max (а_i, b_i, с_i), где i= 1,2, ...,9.
2. Найти номер первого нулевого элемента массива х₁, х₂, ..., х₂₀ и сумму элементов предшествующих ему.
3. Даны три последовательности чисел: а₁, а₂, ..., а₈; b_1, b₂, ..., b₈; с₁, с₂ , ..., с₈. Составить новую последовательность, в которой чередовались бы числа всех трех последовательностей, т.е. d₁ = a₁; d₂=b₁; d₃ = c₁; d₄ = a₂; d₅ = b₂; d₆ = c₂.
4. Известно, что в массиве а₁, а₂, ..., а₁₆ количество отрицательных чисел равно количеству положительных. Составить новый массив так, чтобы чередовались положительные и отрицательные числа.
5. Найти сумму элементов последовательности b₁, b₂, ..., b₁₅ , расположенных правее последнего отрицательного элемента и номер этого элемента.
6. Дана последовательность чисел с₁ , с₂, ..., с₁₆ . Найти произведение элементов этой последовательности до первого нулевого и сумму элементов, расположенных после него.
7. Из массива с₁ , с₂, ..., с₁₈ получить массив х₁ , х₂, ..., х₁₈ по правилу; х₁ = с₁, х₂ =с₃, ..., х₉ =с₁₇, x₁₀=с₁₈ , х₁₁=с₁₆, ..., x₁₈=с₂.
8. Из данного массива чисел х₁ , х₂, ..., х₂₅ исключить последнее положительное число. Оставшиеся числа переписать в новый массив z₁, z₂, ..., z₂₄.
9. Найти номер первого положительного элемента массива b₁, b₂, ..., b₁₅ и сумму элементов, расположенных правее него.
10. Все положительные элементы массива а₁, а₂ , ..., а₂₀, расположенные правее первого нулевого элемента, увеличить в два раза.
11. В массиве х₁ , х₂, ..., х₂₅ поменять местами элементы х₁ , х₄, х₇ , х₁₀, ..., х₂₂ с наименьшим из следующий за ними соответствующей пары элементов.
12. Из заданного массива а₁ , а₂, ..., а₁₂ , не содержащего нулей, получить массив b₁, b₂, ..., b₁₂ , приняв в качестве первых его элементов все положительные элементы массива A с сохранением порядка их следования, а в качестве остальных элементов все отрицательные элементы также с сохранением порядка их следования.
13. Дан массив с₁ , с₂, ..., с₁₅, состоящий из нулей и единиц. Подсчитать количество 0, количество 1 и количество нулей до первой единицы.
14. Дан массив чисел х₁, х₂, ..., х₂₂ . Переписать в другой массив из данного все элементы, расположенные правее последнего отрицательного элемента, сохраняя порядок их следования.
15. По данным числам х, у, z получить массив а₁, а₂, ..., а₁₇ , где а₁ = х, а₂ = у, а₃ = z, а каждый следующий элемент массива определяется как среднее арифметическое трех предшествующих.
16. Из заданных массивов а₁ , а₂, ...а₈; b₁, b₂, ..., b₁₂; с₁ , с₂, ..., с₆ получить массив d₁, d₂, …, d₂₆ в котором разместить сначала все элементы массива A, затем элементы массива B и в конце элементы массива C.
17. В массиве а₁ , а₂, ..., а₁₈ вычислить сумму отрицательных до последнего нулевого и произведение элементов расположенных правее него.
18. В массиве у₁, у₂, ..., у₁₈ элементы с номерами, кратными 4, заменить среднем арифметическим из трех предшествующих элементов.
19. Массивы х₁, х₂, …, х₁₀ и у₁, у₂, ..., у₁₀ преобразовать по правилу: большее из х_i и у_i принять в качестве нового значения х_i , а меньшее – в качестве нового значения у_i (i = 1,2, ...,10).
20. Все элементы массива а₁ , а₂, ..., а₄₅, начиная с первого по порядку положительного элемента, уменьшить на 0,5, если значение элемента превышает 1 и увеличивать на 0,5 в противном случае.
21. В массиве а₁, а₂, ..., а₂₅ найти произведение первых трех положительных элементов.
22. Из десяти последних отрицательных чисел последовательности t₁, t₂, t₃, ..., t₃₀₀ сформировать последовательность у₁, у₂, ..., у₁₀.
23. Если наименьший элемент данной последовательности х₁, х₂, ..., х₂₇ больше 0,1 то все отрицательные элементы последовательности заменить единицей.
24. Дана последовательность а₁, а₂, ..., а₅₀ . Сформировать последовательность в₁, в₂, ..., в₅₀ следующим образом: в начале расположить все отрицательные элементы последовательности, а затем все остальные.

Задачи “Уже проблемы”

1. Дан массив а₁, а₂, ..., a₂₀. Получить массив х₁+у₁ , х₂+у₂, ..., х_r+у_r , где элементами массива х₁, х₂, ..., х_p являются отрицательные, а элементами массива у₁, у₂ , ..., у_t положительные элементы массива A, r = min (р, t).
2. Найти номер первого нулевого элемента массива а₁, а₂, ..., а₂₅ и произведение элементов, расположенных до него, а среди элементов, расположенных правее первого нулевого, найти максимальный элемент.
3. В данном массиве чисел с₁, с₂, ..., с₂₅ поменять местами максимальный элемент с последним отрицательным элементом.
4. Из массива х₁, х₂, ..., х₂₅ сформировать два массива; в одном написать числа, расположенные до минимального элемента массива х, в другой расположенный правее минимального.
5. Пять последних элементов последовательности у₁, у₂, ..., у₄₀ помножить на номер максимального элемента данной последовательности.
6. Из массива а₁, а₂, ..., а₃₀ исключить максимальный элемент.
7. Среди отрицательных элементов массива х₁, х₂, ..., х₅₀ найти минимальный и помножить на него все отрицательные элементы, стоящие левее этого минимального.
8. Дана последовательность чисел d₁, d₂, ..., d₅₀. Найти сумму S₁ элементов до максимального элемента и сумму S₂ элементов, расположенных правее него.
9. В данном массиве чисел а₁, а₂, ..., а₂₅ поменять местами минимальный и максимальный элементы.
10. Найти сумму положительных элементов последовательности d₁, d₂, ..., d₄₀, расположенных до первого нулевого элемента, заменить этой суммой минимальный элемент массива.
11. Из отрицательных элементов массива х₁, х₂ ..., x₃₀, расположенных левее минимального элемента, сформировать новый массив.
12. Из элементов последовательности у₁, у₂, ..., у₂₅, расположенных между первым нулевым и максимальным (в предположении, что в массиве есть положительные числа) (или максимальным и первым нулевым), сформировать новый массив.
13. Дан массив чисел а₁, а₂, ..., а₅₀. Найти сумму элементов массива, стоящих правее первого положительного элемента, и максимальный элемент, его номер среди чисел предшествующих первому положительному.
14. В массиве у₁, у₂, ..., у₂₅ поменять местами минимальный элемент с первым положительным элементом.
15. Среди элементов последовательности а₁, а₂, ..., а₂₅ расположенных до первого отрицательного элемента, найти минимальный элемент. Из положительных элементов массива, расположенных правее минимального, сформировать новый массив.
16. Три отрицательных элемента массива b₁, b₂, ..., b₂₅, расположенных правее максимального помножить на номер максимального элемента.
17. Дан массив х₁, х₂, ..., х₃₀. Помножить элементы массива на квадрат его наименьшего элемента, если х_i больше или равно 0, и на квадрат его наибольшего элемента, если х_i меньше 0.
18. Дана последовательность t₁, t₂, ..., t₂₀. Среди положительных элементов найти максимальный и помножить на него все положительные элементы последовательности.
19. Из элементов последовательности с₁, с₂, с₃ ..., с₄₅, стоящих на нечетных местах и расположенных правее минимального элемента данной последовательности, сформировать новый массив d₁, d₂, …
20. В массиве чисел х₁, х₂, ..., х₁₇ заменить нулем все отрицательные элементы, предшествующие его максимальному элементу.
21. Дана последовательность чисел а₁, а₂, ..., а₂₅; из положительных элементов данной последовательности, расположенных до минимального элемента, сформировать последовательность р₁, p₂, p₃…
22. Из массива у₁, у₂, ..., у₅₀ сформировать новый массив в₁, в₂, в₃, ..., в который записать все числа, находящиеся в массиве у между его максимальным и минимальным (или минимальным и максимальным) элементами.
23. Из массива х₁, х₂, ..., х₃₀ получить массив у₁, у₂, …, у_n состоящий из элементов массива х, расположенных правее его максимального элемента.
24. Если наименьший элемент данной последовательности х₁, х₂, ..., х₂₇ больше 0,1 то все отрицательные элементы последовательности заменить единицей.
25. Найти наименьший элемент из элементов последовательности x₁, x₂, ..., x₂₅, расположенных до первого отрицательного числа. Все отрицательные числа, расположенные правее первого отрицательного, помножить на этот наименьший.
26. В последовательности у₁, у₂, ..., у₂₅ найти максимальный элемент из элементов, стоящих на четных местах. Помножить на него все элементы данной последовательности, стоящие на нечетных местах и расположенные правее найденного максимального.