Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты. В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.

Имеется несколько способов решения параметрических уравнений и неравенств׃ алгебраический, аналитический, функционально-графический. А в некоторых задачах применяются методы математического анализа.

Суть каждого способа рассмотрена на примерах. (Приложение)

1. Алгебраический способ решения иррациональных уравнений с параметрами

Задача 1. При каких уравнение имеет единственное решение?

Решение: 1 способ. Обеспечим неотрицательность обеих частей, возведем в квадрат обе части уравнения:

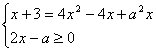
Найдем дискриминант квадратного уравнения:

1) По условию уравнение должно иметь один корень, значит,

но надо проверить, удовлетворяет ли это значение ОДЗ уравнения:

.

2) Если , то только один корень уравнения должен удовлетворять условию .

а)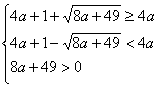

б) 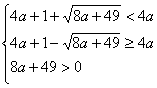Ø

Ответ:

2 способ. Решим это задание аналитическим способом.

Проведем графический анализ менее трудоемкий, чем построение графика - полупараболы с вершиной х=-3; - множество параллельных прямых, с угловым коэффициентом 2.

Рассмотрим схему расположения графиков при различных значениях а, причем с ростом a прямая у=2х - a перемещается вправо.

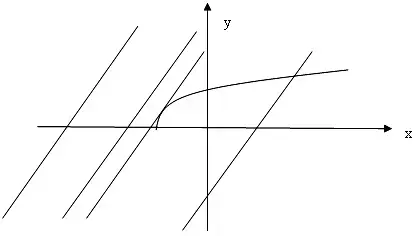
Когда прямая является касательной к полупараболе и, начиная с положения, когда прямая проходит через вершину параболы (- 3; 0),мы имеем одну точку пересечения, т. е одно решение исходного уравнения. Напишем уравнение касательной в точке

Угловой коэффициент равен 2, т. е. =2 , - абсцисса точки касания

Тогда уравнение касательной , a =

При х=-3, у=0 графики пересекаются в двух точках. При этом .

А при имеем одну точку пересечения.

Ответ:

2. Аналитический способ решения тригонометрического уравнения с параметром

Задача 2. При каких значениях параметра a уравнение

имеет на промежутке не меньше 3 корней?

Решение:

1 способ. Заменим , причем |t| ≤ 1

при любом a.

Рассмотрим 2 случая:

1) , тогда уравнения будут иметь не больше 2 корней, но по условию должно быть не меньше 3 корней. Следовательно, этот случай не надо рассматривать.

2) ,

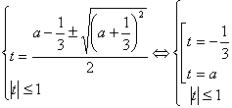
Рассмотрим расположение корней уравнения на тригонометрической окружности.

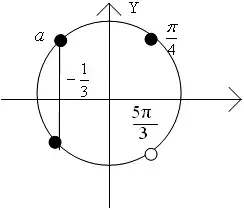
Видим, что при уравнение имеет два решения. Чтобы оно имело не меньше трех решений и .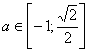

Ответ: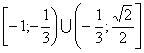

2 способ. Пусть , , тогда . Рассмотрим график .

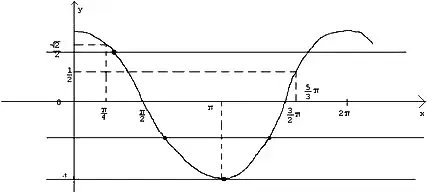
В промежутке при t= - 1 уравнение имеет один корень

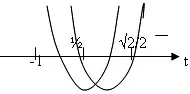
При - два корня, при 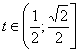- один корень.

Поэтому чтобы исходное уравнение имело не меньше 3 корней необходимо выполнение условия:

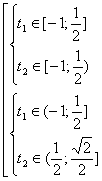	Первая система имеет 4 решения.
	Вторая система имеет 3 решения.

Расположим корни квадратного трехчлена по этим двум условиям:

1)

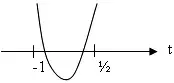
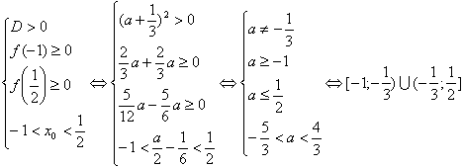
2)

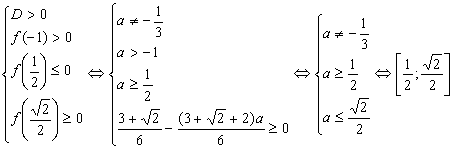
Объединяя 1) и 2) получаем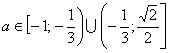

3. Два способа решения одного тригонометрического неравенства с параметром

Задача 3. При каких а неравенство верно для всех х?

Решение: 1 способ. Преобразуем неравенство и приведем его к виду

Пусть. Получим неравенство

Это значит, что парабола при 0≤t≤1 находится ниже оси ох

Рассмотрим 3 случая:

1)

Получаем условия для

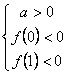
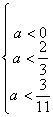
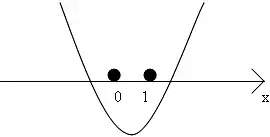
2)

Но если .

Ø

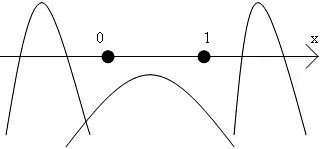
3)

Полученное неравенство верно при любых 0≤t≤1; объединяем 3 случая и получаем ответ: .
2 способ. Уединяем параметр

,

Минимум f(x) достигается при ; т.к - минимум числителя, - максимум знаменателя. Значит,

Максимум f(x) достигается при ; т.е .

Схема:

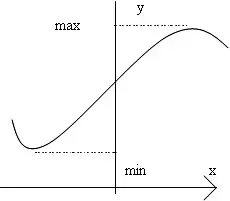
Заметим, что минимум числителя и максимум знаменателя достигается при одном и том же х.

для всех х при

Ответ: .

4. Графически и аналитический способы решения неравенства с параметром, содержащего знак модуля

Задача 5. При каких a неравенство выполняется для всех ?

Решение: . Рассмотрим две функции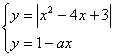

Построим эскизы графиков функций:

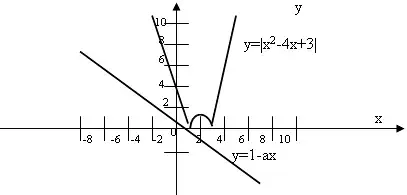
Найдем уравнение касательной в точке функции y= |x2-4x+3|



Тогда . Так как

Подставим значение точки х0 в производную рассматриваемой функции и получаем, что - -a=-2-4, a=4+2.

Следовательно, при a =4+2 y=1-ax - касательная к y=|x2-4x+3|. Значит, чтобы неравенство выполнялось, нужно, чтобы

II способ.

1 случай.

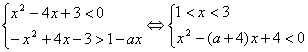
Это значит, что

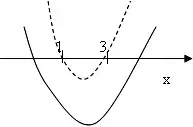
2 случай.

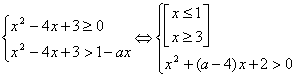
А это значит, что

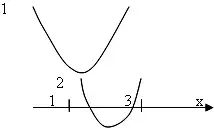
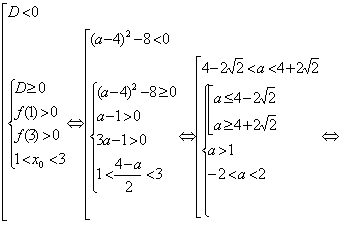
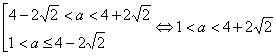
Чтобы неравенство выполнялось при всех x:

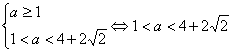
Ответ: .

Решение уравнений и неравенств с параметрами алгебраическим, аналитическим и графическим способами заключается в том, что при одном способе решение может быть громоздким, а при другом - более простым и наглядным. А это говорит о том, что нужно перед началом решения задания оценить его и выбрать тот путь, который проще.

Литература

1. Сборник задач по математике для подготовки к вступительным экзаменам УГНТУ, Уфа-2003 г.
2. Факультативный курс по математике, 10 класс. Шарыгин.И.Ф. Москва «Просвещение» 1989 г.
3. Уравнение с параметрами на факультативных занятиях. С.Я.Постникова. «Математика в школе», №8, 2002 г.
4. Математика абитуриенту. В.В.Ткачук, Москва, 2002 г.

Приложения

• pril.ppt (142.85 КБ)