Урок алгебры по теме "Функция у=aх2+bx+c, ее свойства и график". 8-й класс
Тип урока: урок изучения и закрепления новых знаний.
Цели урока:
- Образовательные: изучить квадратичную функцию, её свойства и график, научиться находить координаты вершины параболы, ось симметрии параболы, научиться строить график квадратичной функции y = ax2 + bx + c;
- Развивающие: способствовать развитию представлений учащихся об особенностях заданий по данной теме, предлагаемых на экзамене по математике в новой форме в 9-м классе, развитию математического кругозора, мышления и речи, внимания;
- Воспитательные: воспитывать умение слушать, анализировать, соблюдать единые требования к оформлению решений, содействовать формированию познавательного интереса к математике.
Формы организации познавательной деятельности: коллективная, индивидуальная, фронтальная, работа в парах.
Оборудование: компьютер, мультимедийный проектор, экран, презентация, карты с опорным конспектом по теме.
ХОД УРОКА
1. Проверка домашнего задания
2. Актуализация знаний
Повторение изученного (фронтальная работа):
- Как построить график функции y = f(x + l), если известен график функции y = f(x)?
- Как построить график функции y = f(x) + m, если известен график функции y = f(x)?
- Как построить график функции y = f(x + l) + m, если известен график функции y = f(x)?
- Какой трёхчлен называется квадратным?
- В чём состоит метод выделения полного квадрата из квадратного трёхчлена?
- Выделите полный квадрат применительно к трёхчлену x2 - 4x + 5.
Ответ: x2 - 4x + 5 = (x2 - 4x + 4) + 1 = (x - 2)2 + 1. (Один ученик решает у доски).
Учитель: Ребята, как вы думаете, чем сегодня на уроке мы с вами будем заниматься?
Учащиеся: Исследованием и построением графиков функций, исследованием их свойств.
Учитель: Действительно, сегодня на уроке мы будем заниматься графиком так называемой квадратичной функции, её свойствами.
3. Объяснение нового материала
(У учащихся на столах карты с опорным конспектом по данной теме).
Итак, рассмотрим многочлен y = ax2 + bx + c, где a, b, c - коэффициенты, причём a ? 0. Такой многочлен называется
квадратным трёхчленом, a - старший коэффициент. Квадратный трехчлен не обязательно может состоять из трёх слагаемых. Например, 5x2 - 3x - квадратный трехчлен, у
которого a = 5, b = - 3, c = 0.
Функция y = ax2 + bx + c, где a, b, c - некоторые произвольные числа, причём a ? 0, называется квадратичной функцией.
Как вы думаете, почему она так называется?
Учащиеся: Возможно потому что x в квадрате.
Учитель: Да, потому что старший член трехчлена содержит переменную x в квадрате.
- Как вы считаете, что будет являться графиком квадратичной функции?
Учащиеся: Графиком квадратичной функции является парабола.
Учитель: Да, вы совершенно правы. Это парабола, которая получается из параболы y = x2 параллельным переносом. Ветви параболы y =
ax2 + bx + c будут направлены вверх, если a > 0, и вниз, если a < 0.
Осью симметрии параболы y = ax2 + bx + c является прямая x = - b/2a, координаты вершины параболы вычисляются по следующим
формулам: x0 = - b/2a, y0 = f(x0).
Учитель: Итак, используя раннее полученные знания и знания, полученные сегодня на уроке, мы сможем построить график любой квадратичной функции. Построить график функции y = 3x2 - 6x + 1.
Задание №1. Построить график функции y = 3x2 - 6x + 1.
Ученики: (один ученик выполняет у доски, остальные на своих местах).
График функции y = 3x2 - 6x + 1 - парабола, ветви которой направлены вверх, т.к. a = 3 > 0.
Найдем координаты вершины параболы: x0 = - b/2a, x0 = 1, y0 = f(x0), y0
= f(1) = 3 • 12 - 6 • 1 + 1 = - 2. Значит, вершина параболы имеет координаты (1; - 2).
Ось симметрии параболы - прямая x= 1.
Построим несколько дополнительных точек, симметричных друг другу относительно оси параболы:
| x | 0 | 2 | -1 | 3 |
| y | 1 | 1 | 10 | 10 |
Соединим полученные точки плавной линией, получим график данной функции.
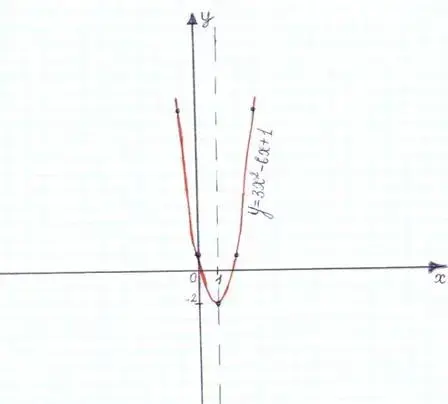
Учитель: Итак, график функции построен. По сути мы построили график функции, используя правило построения графика квадратичной функции, которое называется алгоритмом построения параболы y = ax2 + bx + c. Давайте рассмотрим его. Учебник алгебры стр: 125. (работа с учебником).
Учитель: Итак, ребята, как вы считаете, мы строили график функции y = 3x2 - 6x + 1 так, как это прописано в алгоритме или нет?
Учащиеся: Да.
Учитель: Абсолютно верно, мы использовали при построении графика функции именно этот алгоритм. И в будущем будем пользоваться им. Следующее задание: прочитайте график функции y = 3x2 - 6x + 1, т.е. перечислите по графику свойства функции y = 3x2 - 6x + 1.
Учащиеся: по одному читают свойства функции по построенному графику:
- область определения функции;
- область значений функции;
- промежутки возрастания и убывания функции;
- наименьшее и наибольшее значения функции;
- наибольшее и наименьшее значения функции на отрезке: [0;3].
- и др.
4. Закрепление изученного материала при решении упражнений из задачника: № 22.1 (а,б), № 22.2 (а,б), № 22.5 (а,б), № 22.7 (б). (Коллективная работа).
5. Физкультминутка
6. Проверочная работа по изученному материалу:
| Вариант 1 | Вариант 2 |
|
Задание №1
Какая из данных функций является квадратичной:
|
Задание №1
Какая из данных функций является квадратичной:
|
|
Задание №2
Укажите коэффициенты a, b и c квадратичной функции:
|
Задание №2
Укажите коэффициенты a, b и c квадратичной функции:
|
|
Задание №3
Составьте квадратный трёхчлен y = ax2 + bx + c, у которого a = 2, b = - 1, c = 4. |
Задание №3
Составьте квадратный трёхчлен y = ax2 + bx + c, у которого a = - 1, b = 7, c = 0. |
|
Задание №4
Найдите координаты вершины параболы. Напишите уравнение оси симметрии параболы:
|
Задание №4
Найдите координаты вершины параболы. Напишите уравнение оси симметрии параболы:
|
|
Задание №5
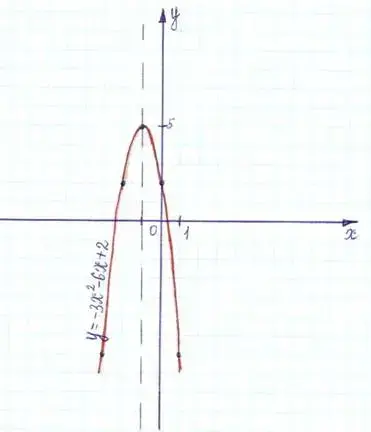
Постройте график функции: y = - 3x2 - 6x + 2. |
Задание №5
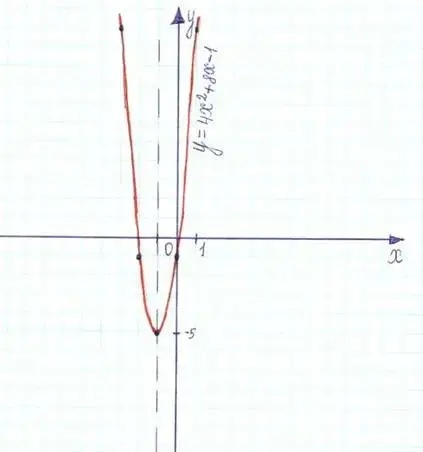
Постройте график функции: y = 4x2 + 8x - 1. |
7. Взаимоконтроль в парах (ответы на экране)
| Вариант 1 | Вариант 2 |
|
Задание №1
а)
|
Задание №1
б)
|
|
Задание №2
Укажите коэффициенты a, b и c квадратичной функции:
|
Задание №2
Укажите коэффициенты a, b и c квадратичной функции:
|
|
Задание №3
2x2 - x + 4. |
Задание №3
- x2 + 7x. |
|
Задание №4
Вершина параболы: (- 1; 5);
|
Задание №4
Вершина параболы: (- 1; - 5);
|
|
Задание №5
|
Задание №5
|
Учитель: Критерии оценивания вы видите на экране:
Оценка «5» - за верно выполненные пять заданий;
Оценка «4» - за верно выполненные любые четыре задания;
Оценка «3» - за верно выполненные любые три задания;
Оценка «2» - в любом другом случае.
Учащиеся: проверяют друг у друга работы, выставляют предварительные оценки. Учитель собирает тетради на проверку.
Учитель: Итак, что вы сегодня узнали на уроке нового? Где вы сможете применить эти знания?
Учащиеся: отвечают на поставленные учителем вопросы.
8. Домашнее задание
§22 с.120-126, опорный конспект, № 22.5 (в,г), № 22.6 (в, г);
проект-исследование: на примере какой - нибудь конкретной квадратичной функции составить проект: построение графика функции и исследование её свойств (в качестве примера квадратичной функции
использовать № 22.7, №22.8).
9. Рефлексия
Учитель: Ребята, используя рефлексивный экран, каждый из вас, выскажите, пожалуйста, своё мнение о нашем уроке, дополнив понравившиеся вам фразы своими мыслями.
У детей на столах отпечатаны карточки в виде парабол с фразами, они заполняют их и прикрепляют на доске в прямоугольной системе координат.
Ребята записывают на своих карточках, некоторые из них читают, что у них получилось, а затем все прикрепляют свои параболы магнитиками к доске.
- сегодня я узнал…
- было интересно…
- было трудно…
- я выполнял задания…
- я понял, что…
- теперь я могу…
- я научился…
- я смог…
- я попробую…
- меня удивило…
- урок дал мне для жизни…
- мне захотелось…
Учитель: Спасибо за урок!
Использованные материалы и интернет-ресурсы.
- Алгебра. 8 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений/ А.Г. Мордкович. - 15-е изд., стер. - М.: Мнемозина, 2013.
- Алгебра. 8 класс. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений/ [А.Г. Мордкович. и др.]; под ред. А.Г. Мордковича. - 15-е изд., стер. - М.: Мнемозина, 2013.
- Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8-го класса. - М.: Илекса, 2005.
- Кузнецова Л.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 кл.- М.: Просвещение, 2007.
- Кочагина М.Н. Математика: 9 класс: Подготовка к «малому ЕГЭ»- М.: Эксмо, 2007.
- Материалы газеты «Первое сентября», 2008-2013гг.
- https://urok.1sept.ru/.