Числовые последовательности
Информационно-целевой блок
Тип урока: урок «открытия» нового знания.
Цель урока: ввести понятие «числовая последовательность», «n-й член последовательности»; познакомить учащихся с видами последовательностей и способами задания последовательности.
Представление о результатах:
Личностные результаты:
- формирование умения сотрудничать со сверстниками в разных социальных ситуациях, умение не создавать конфликтов и находить выходы из спорных ситуаций.
Метапредметные результаты:
- регулятивные: планировать свои действия в соответствии с поставленной задачей и условиями ее реализации;
- познавательные: формирование умений по использованию математических знаний для решения различных математических задач и оценки полученных результатов, по использованию доказательной математической речи при работе с информацией;
- коммуникативные: формирование умений совместно с другими обучающимися находить решение задачи и оценивать полученные результаты.
Предметные результаты:
- понимание сути понятий «числовая последовательность», «члены последовательности», «n-й член последовательности», умение определять n-й член последовательности, понимать и различать виды последовательностей и способы их задания, умение точно и грамотно выражать свои мысли, применяя математическую терминологию, развитие способностей обосновывать рассуждения.
Ресурсы: учебник «Алгебра 9», С.М.Никольский, М.К.Потапов, «Дидактические материалы Алгебра 9 класс», «Просвещение»-2017, карточки с заданиями самостоятельной работы, персональный компьютер (ПК) учителя, интерактивная доска, проектор.
Этапы технологии деятельностного подхода:
- Самоопределение к деятельности (Орг. момент)
- Актуализация знаний (Актуализация знаний)
- Постановка учебной задачи (Мотивация. Постановка проблемы)
- Решение учебной задачи (Заполнение конспекта)
- Первичное закрепление (Решение заданий из ОГЭ)
- Включение в систему знаний, повторение (Рефлексия)
- Домашнее задание
Организационная структура урока
Описание этапов
1. Актуализация знаний
Здравствуйте, ребята.
«Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применима к явлениям действительного мира»
М.В.Лобачевский
Сегодня мы приступим к изучению одной из самых интересных темы алгебры 9 класса. Для этого нужно определить тему урока.

2. Мотивация
На уроке мы познакомимся с понятием «числовая последовательность», рассмотрим виды последовательностей и способы их задания.
Формулирование обучающимися темы и целей урока.
- О чем пойдет речь на уроке?
- Что должны узнать?
- Чему должны научиться?
- Что такое, по-вашему, мнению, «Последовательность»?
- Что такое числовая последовательность?
- Обозначение числовой последовательности.
- Какие последовательности существуют?
- Назовите способы задания последовательности.
3. Заполнение конспекта. Решение задач
Последовательности составляют такие элементы природы, которые можно пронумеровать! Какие события в нашей жизни происходят последовательно? Приведите примеры таких явлений и событий.
Например, дни недели, названия месяцев, возраст человека, номер счёта в банке, последовательно происходит смена дня и ночи, последовательно увеличивает скорость автомобиль, последовательно пронумерованы дома на улице и т.д.
Последовательный - 1. Непрерывно следующий за другим. 2. Логически обоснованный, закономерно вытекающий из чего-нибудь. сущ. Последовательность. (Толковый словарь русского языка. С.И.Ожегов).
Последовательность - упорядоченный набор чисел. (Справочное издание. Математика).
Определение. Числовая последовательность - числа, образующие последовательность, называют соответственно первым, вторым, третьим…. n-м членом последовательности.

В течение урока вы будете заполнять опорный конспект по теме «Числовые последовательности».
Задание 1. Рассмотрите предложенные ряды чисел
А) 0; 2; 4; 6; 8; 10; …
Б) 1; 2; 3; 4; 5; 6; 7; 8; 9.
В) -10; -12; -14; -16; …
Г) -3; -6; -12; -24; -48;…
Д) 10; 11; 12;…; 98; 99.
Е)100; 50; 25; 12,5; 6,25; 3,125; …
Ж) 7; 7; 7; 7;…
- Можно ли данные ряды назвать числовыми последовательностями?
- Разделите их на группы. На сколько групп разделили? Как можно назвать каждую группу?
Виды числовых последовательностей:
- Бесконечные (бесконечное число членов);
- Конечные (конечное число членов);
- Убывающие (каждый последующий член меньше предыдущего);
- Возрастающие (каждый последующий член больше предыдущего);
- Стационарная (постоянная) - (каждый последующий член равен предыдущему).
Задание 2. Определите следующий член последовательности
А) 0; 2; 4; 6; 8; 10; …
Б) -10; -12; -14; -16; …
В) -3; -6; -12; -24; -48;…
Г) 100; 50; 25; 12,5; 6,25; 3,125; …
Способы задания числовой последовательности:
Словесный способ. Представляет собой закономерность или правило расположения членов последовательности, описанный словами.
Пример 1: Записать последовательность, все члены которой с нечётными номерами равны -10, а с чётными номерами равны 10.
Аналитический способ. Последовательность задается формулой n-го члена: Хn= 3n + 2. По этой формуле можно найти любой член последовательности.
Пример 2: Вычислите первые четыре члена этой последовательности.
а1 = 4+2·(1+1)=8
а2 = 4+2·(2+1)= 10
а3 = 4+2·(3+1)= 12
а4 = 4+2·(4+1)=14
Графический способ. Числовая последовательность задается графиком, который представляет собой изолированные точки. Абсциссы этих точек - натуральные числа: n = 1; 2; 3; 4; ... . Ординаты - значения членов последовательности: a1; a2; a3; a4;…
Пример 3: Рассмотрим функцию

Рекуррентный способ. Задается формула, по которой каждый следующий член находят через предыдущие члены.
Указывается правило позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. При вычислении членов последовательности по этому правилу мы все время возвращаемся назад, выясняем чему равны предыдущие члены, поэтому такой способ называют рекуррентным (от латинского recurrere - возвращаться).
Решите задачу: В январе вам подарили пару новорожденных кроликов. Через два месяца у них рождается новая пара кроликов, в следующем месяце - еще одна пара и т.д. ежемесячно. С
каждой новой парой кроликов происходит то же самое. Сколько пар кроликов будет у вас в декабре, если ни одна пара не погибнет?
Разгадкой стал числовой ряд, каждое последующее число которого, является суммой двух предыдущих.
| Месяцы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Пары кроликов |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
233 |
377 |
Отслеживая каждый месяц количество пар кроликов, мы получили такой ряд чисел: 1,1,2,3,5,8,13,21,34,55,89,144,233,377
Ответ: 144 пар кроликов.
Решая задачу о размножении кроликов, Леонардо описал бесконечную числовую последовательность, любой член которой, начиная с третьего, выражается через предыдущие числа. В честь автора этой задачи вся последовательность называется рядом Фибоначчи, а члены её - числами Фибоначчи. С тех пор, как Фибоначчи открыл свою последовательность, были найдены много явлений природы, в которых его последовательность чисел прослеживается очень четко. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи. Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис - листорасположение), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд чисел Фибоначчи.
Задание 3. Составьте для каждой последовательности рекуррентную формулу
А) 0; 2; 4; 6; 8; 10; …
Б) -10; -12; -14; -16; …
В) -3; -6; -12; -24; -48;…
Г) 100; 50; 25; 12,5; 6,25; 3,125; …
Задание 4. y1 =3, yn = yn-1 + 4, если n = 2, 3, 4, …
Решение: Каждый член последовательности получается из предыдущего прибавлением к нему числа 4
y1 = 3
y2 = y1 + 4= 3 + 4 = 7
y3= y2+ 4= 7 + 4 = 11
y4 = y3 + 4= 11 + 4 = 15 и т.д.
Получаем последовательность 3, 7, 11, 15, 19, 23, 27, …
Задание 5: Выписать первые пять членов последовательности аn если аn =7 an+1 = 5 + аn
Решение:
а1+1 = 5+ аn
a2 = 5+ 7 = 12,
a3= 5+ 12 = 17,
a4 = 5+ 17 = 22,
a5 = 5+ 22 = 27
Ответ: 27
Выделяют 2 особенно важные рекуррентно заданные последовательности:
- Арифметическая прогрессия
у1 = а, уn = уn-1 + d, а и d - числа, n = 2, 3, …
- Геометрическая прогрессия
у1 = b, уn = уn-1 · q, b и q - числа, n = 2, 3, …
Закрепление изученного материала. Решение задач из учебника: (б,г,е), №415 (а,б), №416 (а), №420
Решение задач из ОГЭ (учебник Математика. 3000 задач с ответами. Все задания 1 части. Под ред. Ященко И.В.)
№1275. Последовательность задана формулой ![]() . Какое из указанных чисел является членом этой последовательности?
. Какое из указанных чисел является членом этой последовательности?
1) -56
2) -58
3) -57
4) -55
Решение:
Рассмотрим несколько первых членов последовательности
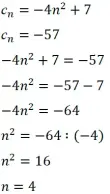
Остальные числа при подставлении не целые и отрицательные числа, а порядковый номер не может быть таковым.
Ответ: 3.
Задание 11 из ОГЭ (2 ученика решают на доске).

4. Рефлексия
Выработка собственного отношения к изучаемому материалу.
Проведение рефлексии с применением вопросов.
- Что нового вы узнали?
- Чему научились?
- Где в жизни вам могут пригодиться эти знания?
- Кому из вас было трудно?
- Кому помогли товарищи?
5. Домашнее задание
Глава 3 п.6.1 №422, №423, №426.
Используемая литература
- Алгебра. 9 класс: учебник для общеобразовательных организаций / [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]. - М.: Просвещение, 2016
- Алгебра. Дидактические материалы, 9 класс./ М.К.Потапов, А.В.Шевкин. - 2-е изд. - М.: Просвещение, 2016.
- Алгебра. Методические рекомендации. 9 класс: учебное пособие для общеобразовательных организаций / М.К.Потапов, А.В.Шевкин. - М.: Просвещение, 2017.
- Тематические тесты. Алгебра 9. П.В.Чулков, Т.С.Струков, Изд-во М. «Просвещение», 2016.
- ГИА. 3000 задач с ответами по математике. Все задания части 1. Под ред. А.Л.Семенова, И.В.Ященко, разработано МИОО, - М.: «Экзамен» МЦНМО, 2019.