Урок по теме "Сложение и умножение числовых неравенств"

Тип урока:  урок изучения и первичного закрепления новых знаний

Цель: рассмотреть теоремы о почленном сложении и умножении числовых неравенств; сформировать навыки применения их к решению простейших задач на оценку выражений; закрепить свойства неравенств.

Оборудование: проектор, учительский компьютер, интерактивная доска, компьютеры для учеников.

ХОД УРОКА

1. Организационный момент

2. Проверка домащнего задания

Решение показывается на интерактивной доске с помощью проектора и компьютера. (слайды № 3-5)

3. Устная работа

Оцените значение выражений и заполните пропуски, напишите знаки сравнения.

1. Если x > – 3, то (слайд 6)

2. Если  – 2 < x < 4, то (слайд 7)

4. Изучение нового материала

Теперь давайте рассмотрим теоремы о почленном сложении и умножении числовых неравенств. (слайд № 8)

Теорема 5.  Если почленно сложить верные неравенства одного знака, то получится верное неравенство.

Если a < b и  c < d, то a + c < b + d

Доказательство (проводится с помощью обучающихся на интерактивной доске).
Прибавим к обеим частям неравенства a < b  число c, получим  a + c < b + c
Прибавим к обеим частям неравенства c < d  число b, получим  b + c < b + d
Из неравенств a + c < b + c и b + c < b + d  следует, что a + c < b + d.

Пример 1. Сложите числовые неравенства:

   3 < 7
+
   6 < 9   
9 < 16

Теорема 6.  Если перемножить почленно верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.

Если  a < b и  c < d, где a, b, c, d – положительные числа, то aс < bd.

Доказательство (проводится с помощью обучающихся на интерактивной доске)

Умножим обе части неравенства a < b  на положительное число c, получим aс < bd. Умножим обе части неравенства c< d  на положительное число b, получим bс < bd. Из неравенств ac < bc и  bc< bd,  следует, что aс < bd

Пример 1. Сложите числовые неравенства:

  3 < 7
x
   6 < 9
 18 < 63

Следствие. Если a > b и a, b – положительные числа, то > , где n – натуральное число.

Заметим, что все рассмотренные свойства неравенств справедливы и в случае нестрогих неравенств:

если a > b и c  > d, то a + c > b + d;
если a > b, c > d и a, b, c, d – положительные числа, то ac > bd;
если a > b и a, b – положительные числа, то , где n – натуральное число.

Часто значения величин, являющихся результатами измерений, не точны. Измерительные приборы, как правило, позволяют лишь установить границы, между которыми находится точное значение.
Пусть, например, в результате измерения ширины x и длины y прямоугольника было установлено, что 2,5 см < x < 2,7 см и 4,1 см < y < 4,3 см. Тогда с помощью теоремы 6 можно оценить площадь прямоугольника. Имеем:

   2,5 см < x < 2,7 см
х
   4,1 см < y < 4,3 см
10,25 см² < xy < 11,61 см².

Вообще, если известны значения границ величин, то, используя свойства числовых неравенств, можно найти границы значения выражения, содержащего эти величины, т. е. оценить его значение.

5. Физкультминутка (видеофизкультминутка)

6. Закрепление изученного материала

Обучающиеся решают на доске с комментариями.
Задания из дидактического материала: С-34, стр.84

1. Сложите почленно неравенства:

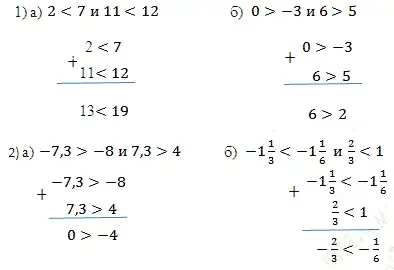
3. Перемножьте почленно неравенства:

№ 768.

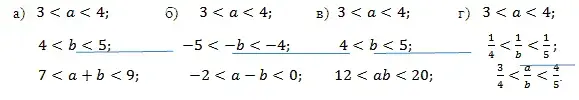
7. Самостоятельная работа (с выставлением оценки) (слайд №10)

Самостоятельна работа проводится в виде сопоставления правильных решений с заданием в программе MyTestX за компьютером. (Приложение 1)

8. Итоги урока (слайд №11)

1. Сформулируйте теорему о почленном сложении числовых неравенств.
2. Сформулируйте теорему о почленном умножении числовых неравенств.
3. Как вы думаете, данные теоремы справедливы только для двух числовых неравенств?
4. Что значит оценить значение выражения?

9. Домашнее задание

Д.м. С-34, стр.35: №№1, 2, учебник: №769.(слайд № 12)

10. Рефлексия

Ученикам предлагается закончить предложения: (слайд №13)

Я сегодня познакомился с ...
У меня сегодня получилось ...
Но, хотелось бы ...