Образовательные цели урока.
Сформировать понятие полярной системы
координат
Изучение данной темы рекомендуется проводить после знакомства с графическими возможностями Visual Basic, изучения построения графиков функций в прямоугольной системе координат. Изложение материала сопровождается показом презентации (Презентация).
1. Понятие полярной системы координат. (Слайд 1)
Суть задания какой-либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. Например, в декартовой прямоугольной системе это координаты точки (x, y).
Любая точка на плоскости может быть однозначно определена в различных системах координат. Выбор системы координат зависит от нескольких факторов, например, от способа задания начальных значений при решении задачи, от наглядности представления результата. В некоторых случаях вычисления удобнее проводить в системе координат, отличной от декартовой прямоугольной системы. Существует множество различных систем координат: косоугольная, цилиндрическая, сферическая, биполярная, полярная, прямоугольная и др.
Одной из наиболее часто используемых наряду с декартовой является полярная система координат.
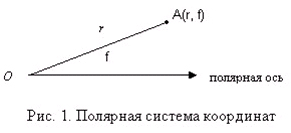
Полярная система координат образуется полярным полюсом О и полярной осью, которая представляет луч, проведённый из полюса в направлении слева направо (Рис. 1).
В полярной системе координат любой точке (например, т. А) соответствует единственная пара полярных координат А(r, f), где r – полярный радиус, f – полярный угол. Таким образом, по заданной паре полярных координат можно однозначно определить положение точки на плоскости.
Полярный радиус r – отрезок, соединяющий полюс с заданной точкой А.
Полярный угол f - угол между полярной осью и полярным радиусом. За положительное направление полярного угла f примем направление против часовой стрелки.
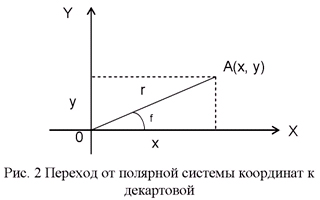
Для перехода от полярных координат к декартовым (слайд 2) нужно совместить полярную и декартову прямоугольную сиcтемы таким образом, чтобы начала их координат совпадали, а полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы координат. (Рис. 2).
Тогда получим формулы перехода от полярных координат (r, а) к декартовым (х, у):
x = r*cos f
у = r*sin f
Эти уравнения называются параметрическими.
Формулы обратного перехода от декартовых координат к полярным:
r =![]()
f = arctg (y/x)
2. Практическая работа. Построение графиков полярных кривых по параметрическим уравнениям
Задание. (Слайд 3)
Создать проект в среде Visual Basic для построения полярных кривых: кардиоиды, логарифмической спирали, Декартова листа, фигуры Лиссажу, k-лепестковой розы, эпициклоиды, заданных параметрическими уравнениями.
Параметрические уравнения полярных кривых:
1) Кардиоида
a = 4
r = a * (1 + Cos(f))
x = r * Cos(f)
y = r * Sin(f)
f I [0, 2*p ]
2) Логарифмическая спираль
a = 0.2; n = 5; b = 0.15
r = a * Exp(b * f)
x = r * Cos(f)
y = r * Sin(f)
f I [0, 2*p *n]
3) Декартов лист
a = 4
r = 3 * a * Cos(f) * Sin(f) / (Cos(f) ^ 3 + Sin(f) ^ 3)
x = r * Cos(f)
y = r * Sin(f)
f I [0, 2*p ]
4) Фигура Лиссажу
r = 5
x = r * Cos(3 * f)
y = r * Sin(2 * f)
f I [-p , p ]
5) k-лепестковая роза
При чётных значениях k получается 2*k-лепестковая роза, а при нечётных значениях – k-лепестковая роза.
r = Sin(k * f)
x = 10 * r * Cos(f)
y = 10 * r * Sin(f)
f I [-p ,p ]
6) Эпициклоида
x = (a + b) * Cos(f) - a * Cos((a + b) * f / a)
y = (a + b) * Sin(f) - a * Sin((a + b) * f / a)
f I [0, 2*p ]
Значение b вводится с клавиатуры. Значение a примем равным a = b / 3.
Решение.
1. Разработка интерфейса проекта (Рис. 3). (Слайд 4)
Для выбора типа полярной кривой создадим массив переключателей Option1, который разместим в контейнере Frame1. Для построения графика разместим на форме графическое окно Picture1. Для вывода названия графика и параметрических уравнений создадим метку Label2 и текстовое поле Text1. Для управления проектом создадим 3 командные кнопки Command1, Command2, Command3 (Пуск, Сброс, Выход).
Интерфейс проекта представлен на рис. 3.
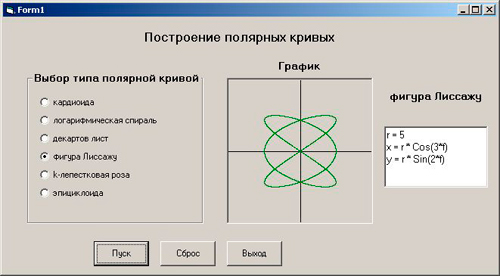
Рис.3. Интерфейс проекта
2. Для созданных элементов управления установим свойства, приведенные в таблице. (Слайды 5, 6)
Свойства элементов управления
| Элемент управления | Свойство | Значение |
| Frame1 | Caption | Выбор типа полярной кривой |
| Option1(0) | Caption | кардиоида |
| Option1(1) | Caption | логарифмическая спираль |
| Option1(2) | Caption | декартов лист |
| Option1(3) | Caption | k-лепестковая роза |
| Option1(4) | Caption | фигура Лиссажу |
| Option1(5) | Caption | эпициклоида |
| Label3 | Caption | Построение полярных кривых |
| Label1 | Caption | График |
| Label2 | Caption | |
| Label1, Label2, Label3 | Alignment | 2 - center |
| Text1 | Text | |
| Text1 | Alignment | 0 - left |
| Picture1 | FillStyle | 0 - solid |
| Command1 | Caption | Пуск |
| Command2 | Caption | Выход |
| Command3 | Caption | Сброс |
3. Описание переменных. (Слайд 7)
x, y – координаты точки, f - угол, r – радиус, a, b, k, q - коэффициенты уравнений, z - переменная для хранения индекса выбранного переключателя, i – параметр цикла для задержки изображения, pi – число Пи.
В разделе описаний опишем типы выбранных переменных.
Dim z, k As Integer, f, pi, a, r, b, q As Single, i As Long, x, y As Single
4. Разработка программного кода. (Слайды 8-13)
Программный код проекта полностью приведён в Приложении 1.
Создадим процедуру переключателя Option1_Click для выбора типа полярной кривой. Для этого нужно проанализировать значение свойства Value. У включенного переключателя Value=True. В переменной z запоминаем индекс выбранного переключателя.
По кнопке Пуск в зависимости от значения z строим графики полярных кривых. Рассмотрим построение графиков на примере кардиоиды, фигуры Лиссажу и эпициклоиды. Графики остальных кривых вы построите самостоятельно.
Графики полярных кривых и параметрические уравнения приведены на слайдах 14-18.
Задания для самостоятельной работы. (Слайды 19-22)
Литература
- Глушаков С.В., Мельников В.В., Сурядный А.С. Программирование в среде Windows. Visual Basic 6.0. М.: ООО “Издательство АСТ”, 2001.
- Браун С. Visual Basic. Учебный курс. – Спб.: Питер, 2002.
- Есипов А.С., Паныгина Н.Н., Громада М.И. Информатика. Задачник. – СПб: Наука и техника, 2001.
- Журнал “Информатика и образование”, № 2/2005.