Понятие функции и всё, что с ним связано, относится к традиционно сложным, не
до конца понятым. Особым камнем преткновения при изучении функции и подготовке к
ЕГЭ являются область определения и область значений (изменения) функции.
Нередко учащиеся не видят разницы между областью определения функции и областью
её значений.
И если задачи на нахождение области определения функции учащимся удаётся
освоить, то задачи на нахождение множества значений функции вызывают у них
немалые затруднения.
Цель данной статьи: ознакомление с методами нахождения значений функции.
В результате рассмотрения данной темы был изучен теоретический материал,
рассмотрены способы решения задач на нахождение множеств значений функции,
подобран дидактический материал для самостоятельной работы учащихся.
Данная статья может быть использована учителем при подготовке учащихся к
выпускным и вступительным экзаменам, при изучении темы “Область значения
функции” на факультативных занятиях элективных курсах по математике.
I. Определение области значений функции.
Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y0, для каждого из которых найдётся такое число x0, что: f(x0) = y0.
Напомним области значений основных элементарных функций.
Рассмотрим таблицу.
| Функция | Множество значений |
| y = kx+ b | E(y) = (-∞;+∞) |
| y = x2n | E(y) = [0;+∞) |
| y = x2n +1 | E(y) = (-∞;+∞) |
| y = k/x | E(y) = (-∞;0)u(0;+∞) |
| y = x1/2n | E(y) = [0;+∞) |
| y = x1/2n+1 | E(y) = (-∞;+∞) |
| y = ax | E(y) = (0;+∞) |
| y = logax | E(y) = (-∞;+∞) |
| y = sin x | E(y) = [-1;1] |
| y = cos x | E(y) = [-1;1] |
| y = tg x | E(y) = (-∞;+∞) |
| y = ctg x | E(y) = (-∞;+∞) |
| y = arcsin x | E(y) = [-π/2; π/2] |
| y = arcos x | E(y) = [0; π] |
| y = arctg x | E(y) = (-π/2; π/2) |
| y = arcctg x | E(y) = (0; π) |
Заметим также, что областью значения всякого многочлена чётной степени является промежуток [m;+∞) , где m – наименьшее значение этого многочлена, либо промежуток
(-∞;n] , где n – наибольшее значение этого многочлена.
II. Свойства функций, используемые при нахождении области значений функции
Для успешного нахождения множества значений функции надо хорошо знать свойства основных элементарных функций, особенно их области определения, области значений и характер монотонности. Приведём свойства непрерывных, монотонных дифференцируемых функций, наиболее часто используемые при нахождении множества значений функций.
- Если функция f(x) непрерывна и возрастает на отрезке [a;b], то множество
значений функции на этом отрезке есть отрезок [f(a),f(b)]. При этом каждое
значение А
 [f(a),f(b)] функция принимает ровно при одном значении x принадлежит [a,b],
т.е уравнение f(x) = А имеет единственный корень на отрезке [a,b]. Если же f(x)
– непрерывная и убывающая на отрезке [a,b] функция, то её множество значений
на [a,b] есть отрезок [f(a),f(b)].
[f(a),f(b)] функция принимает ровно при одном значении x принадлежит [a,b],
т.е уравнение f(x) = А имеет единственный корень на отрезке [a,b]. Если же f(x)
– непрерывная и убывающая на отрезке [a,b] функция, то её множество значений
на [a,b] есть отрезок [f(a),f(b)]. - Если функция f(x) непрерывна на отрезке [a,b] и m = min f(x), M = max f(x) – её наименьшее и наибольшее значение на этом отрезке, то множество значений f(x) на [a,b] есть отрезок [m;M].
- Если функция непрерывна на отрезке [a,b] и дифференцируема (имеет производную) в интервале (a,b), то наибольшее и наименьшее значения функции на отрезке [a,b] существуют и достигаются либо на концах отрезка, либо в критических точках функции, расположенных на отрезке
Свойства 2 и 3, как правило, используются вместе свойством элементарной функции быть непрерывной в своей области определения. При этом наиболее простое и краткое решение задачи на нахождение множества значений функции достигается на основании свойства 1, если несложными методами удаётся определить монотонность функции. Решение задачи ещё упрощается, если функция, вдобавок, – чётная или нечётная, периодическая и т.д. Таким образом, при решении задач на нахождение множеств значений функции следует по мере надобности проверять и использовать следующие свойства функции:
- непрерывность;
- монотонность;
- дифференцируемость;
- чётность, нечётность, периодичность и т.д.
Несложные задачи на нахождение множества значений функции в большинстве своём ориентированны:
а) на использование простейших оценок и ограничений: (2х>0, -1≤sinx?1, 0≤cos2x?1 и т.д.);
б) на выделение полного квадрата: х2 – 4х + 7 = (х – 2)2+ 3;
в) на преобразование тригонометрических выражений: 2sin2x – 3cos2x + 4 = 5sin2x +1;
г) использование монотонности функции x1/3 + 2x-1 возрастает на R.
III. Рассмотрим способы нахождения областей значений функций.
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.
Раскроем суть этих методов на конкретных примерах.
Пример 1. Найдите область значений E(y) функции y = log0,5(4 – 2·3x – 9x).
Решим этот пример методом последовательного нахождения значений сложных аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
y = log0,5(5 – (1 + 2·3x – 32x)) = log0,5(5 – (3x + 1)2)
И последовательно найдём множества значений её сложных аргументов:
E(3x) = (0;+∞), E(3x+ 1) = (1;+∞), E(-(3x+ 1)2 = (-∞;-1), E(5 – (3x+1)2) = (-∞;4)
Обозначим t = 5 – (3x+1)2, где -∞≤t≤4. Тем самым задача сводится к нахождению множества значений функции y = log0,5t на луче (-∞;4). Так как функция y = log0,5t определена лишь при, то её множество значений на луче (-∞;4) совпадает со множеством значений функции на интервале (0;4), представляющем собой пересечение луча (-∞;4) с областью определения (0;+∞) логарифмической функции. На интервале (0;4) эта функция непрерывна и убывает. При t > 0 она стремится к +∞, а при t = 4 принимает значение -2, поэтому E(y) = (-2, +∞).
Пример 2. Найдите область значений функции
y = cos7x + 5cosx
Решим этот пример методом оценок, суть которого состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Из неравенств -1≤cos7x?1, -5≤5cosx?5 получим оценку -6≤y?6. При x = р и x = 0 функция принимает значения -6 и 6, т.е. достигает нижней и верхней границы оценки. Как линейная комбинация непрерывных функций cos7x и cosx, функция y непрерывна на всей числовой оси, поэтому по свойству непрерывной функции она принимает все значения с -6 до 6 включительно, и только их, так как в силу неравенств -6≤y?6 другие значения у неё невозможны. Следовательно, E(y) = [-6;6].
Пример 3. Найдите область значений E(f) функции f(x) = cos2x + 2cosx.
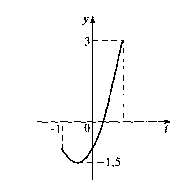
По формуле косинуса двойного угла преобразуем функция f(x) = 2cos2x + 2cosx – 1 и обозначим t = cosx. Тогда f(x) = 2t2 + 2t – 1. Так как E(cosx) =
[-1;1], то область значений функции f(x) совпадает со множеством значений функции g(t) = 2t2 + 2t – 1 на отрезке [-1;1], которое найдём графическим методом. Построив график функции y = 2t2 + 2t – 1 = 2(t + 0,5)2 – 1,5 на промежутке [-1;1], находим E(f) = [-1,5; 3].
Замечание – к нахождению множества значений функции сводятся многие задачи с параметром, связанные, в основном, с разрешимостью и числом решений уравнения и неравенств. Например, уравнение f(x) = а разрешимо тогда и только тогда, когда
a
![]() E(f) Аналогично, уравнение f(x) = а имеет хотя бы один корень,
расположенный на некотором промежутке Х, или не имеет ни одного корня на этом
промежутке тогда и только тогда, когда а принадлежит или не принадлежит
множеству значений функции f(x) на промежутке Х. Также исследуются с
привлечением множества значений функции и неравенства f(x)≠ а, f(x)>а
и т.д. В частности, f(x)≠ а для всех допустимых значений х, если
a
E(f) Аналогично, уравнение f(x) = а имеет хотя бы один корень,
расположенный на некотором промежутке Х, или не имеет ни одного корня на этом
промежутке тогда и только тогда, когда а принадлежит или не принадлежит
множеству значений функции f(x) на промежутке Х. Также исследуются с
привлечением множества значений функции и неравенства f(x)≠ а, f(x)>а
и т.д. В частности, f(x)≠ а для всех допустимых значений х, если
a
![]() E(f)
E(f)
Пример 4. При каких значениях параметра а уравнение (x + 5)1/2 = a(x2 + 4) имеет единственный корень на отрезке [-4;-1].
Запишем уравнение в виде (x + 5)1/2 / (x2 + 4) = a . Последнее уравнение имеет хотя бы один корень на отрезке [-4;-1] тогда и только тогда, когда а принадлежит множеству значений функции f(x) = (x + 5)1/2 / (x2 + 4) на отрезке [-4;-1]. Найдём это множество, используя свойство непрерывности и монотонности функции.
На отрезке [-4;-1] функция y = xІ + 4 непрерывна, убывает и положительна, поэтому функция g(x) = 1/(x2 + 4) непрерывна и возрастает на этом отрезке, так как при делении на положительную функцию характер монотонности функции меняется на противоположный. Функция h(x) = (x + 5)1/2 непрерывна и возрастает в своей области определения D(h) = [-5;+∞) и, в частности на отрезке [-4;-1], где она, кроме того, положительна. Тогда функция f(x)=g(x)·h(x), как произведение двух непрерывных, возрастающих и положительных функций, также непрерывна и возрастает на отрезке [-4;-1], поэтому её множество значений на [-4;-1] есть отрезок [f(-4); f(-1)] = [0,05; 0,4]. Следовательно, уравнение имеет решение на отрезке [-4;-1], причём единственное (по свойству непрерывной монотонной функции), при 0,05 ≤ a ≤ 0,4
Замечание. Разрешимость уравнения f(x) = a на некотором промежутке Х равносильна принадлежности значений параметра а множеству значений функции f(x) на Х. Следовательно, множество значений функции f(x) на промежутке Х совпадает с множеством значений параметра а, для которых уравнение f(x) = a имеет хотя бы один корень на промежутке Х. В частности, область значений E(f) функции f(x)совпадает с множеством значений параметра а, для которых уравнение f(x) = a имеет хотя бы один корень.
Пример 5. Найдите область значений E(f) функции
![]()
Решим пример методом введения параметра, согласно которому E(f) совпадает с множеством значений параметра а, для которых уравнение
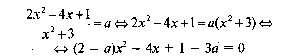
имеет хотя бы один корень.
При а=2 уравнение является линейным – 4х – 5 = 0 с ненулевым коэффициентом при неизвестной х , поэтому имеет решение. При а≠2 уравнение является квадратным, поэтому оно разрешимо тогда и только тогда, когда его дискриминант
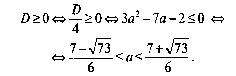
Так как точка а = 2 принадлежит отрезку
![]() то
искомым множеством значений параметра а, значит, и областью значений E(f)
будет весь отрезок.
то
искомым множеством значений параметра а, значит, и областью значений E(f)
будет весь отрезок.
Как непосредственное развитие метода введения параметра при нахождении множества значений функции, можно рассматривать метод обратной функции, для нахождения которой надо решить относительно х уравнение f(x)= y, считая y параметром. Если это уравнение имеет единственное решение x =g(y), то область значений E(f) исходной функции f(x) совпадает с областью определения D(g) обратной функции g(y). Если же уравнение f(x)= y имеет несколько решений x =g1(y), x =g2(y) и т.д., то E(f) равна объединению областей определений функции g1(y), g2(y) и т.д.
Пример 6. Найдите область значений E(y) функции y = 52/(1-3x).
Из уравнения
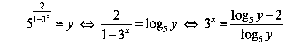
найдём обратную функцию x = log3((log5y – 2)/(log5y)) и её область определения D(x):
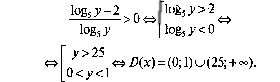
Так как уравнения относительно х имеет единственное решение, то
E(y) = D(x) = (0; 1)![]() (25;+∞).
(25;+∞).
Если область определения функции состоит из нескольких промежутков или функция на разных промежутках задана разными формулами, то для нахождения области значений функции надо найти множества значений функции на каждом промежутке и взять их объединение.
Пример 7. Найдите области значений f(x) и f(f(x)), где
![]()
Найдём сначала множество значений функции f(x) на луче (-∞;1], где она совпадает с выражением 4x + 9·4-x + 3. Обозначим t = 4x . Тогда f(x) = t + 9/t + 3, где 0 < t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x) на луче (-∞;1] совпадает с множеством значений функции g(t) = t + 9/t + 3, на промежутке (0;4], которое найдём, используя производную g’(t) = 1 – 9/t2. На промежутке (0;4] производная g’(t) определена и обращается там в нуль при t = 3. При 0<t<3 она отрицательна, а при 3<t<4 положительна. Следовательно, в интервале (0;3) функция g(t) убывает, а в интервале (3;4) она возрастает, оставаясь непрерывной на всём промежутке (0;4), поэтом g(3)= 9 – наименьшее значений этой функции на промежутке (0;4], в то время как её наибольшее значение не существует, так при t→0 справа функция g(t)→+∞. Тогда, по свойству непрерывной функции, множеством значений функции g(t) на промежутке (0;4], а значит, и множеством значений f(x) на (-∞;-1], будет луч [9;+∞).
При х >1 функция f(x) совпадает с выражением 2cos(x-1)1/2 + 7. Квадратный корень (x-1)1/2 при x > 1 определён и принимает все положительные значения, поэтому cos(x-1)1/2 принимает все значения от -1 до 1 включительно, а выражение 2cos(x-1)1/2 + 7 принимает все значения от 5 до 9 включительно. Следовательно, множеством значений функции f(x) на луче (1;+∞) будет отрезок [5;9].
Теперь, объединив промежутки [9;+∞) и [5;9] – множества значений функции f(f(x)),
обозначим t = f(x). Тогда f(f(x)) = f(t), где
![]() При указанных t функция f(t) = 2cos(x-1)1/2 + 7
и она снова принимает все значения от 5 до 9 включительно, т.е. область значений
E(fІ) = E(f(f(x))) = [5;9].
При указанных t функция f(t) = 2cos(x-1)1/2 + 7
и она снова принимает все значения от 5 до 9 включительно, т.е. область значений
E(fІ) = E(f(f(x))) = [5;9].
Аналогично, обозначив z = f(f(x)), можно найти область значений E(f3) функции f(f(f(x))) = f(z), где 5 ≤ z ≤ 9 и т.д. Убедитесь, что E(f3) = [2cos81/2 + 7; 2cos2 + 7].
Наиболее универсальным методом нахождения множества значений функции является использование наибольшего и наименьшего значений функции на заданном промежутке.
Пример 8. При каких значениях параметра р неравенcтво 8x-р ≠ 2x+1 – 2x выполняется для всех -1 ≤ x < 2.
Обозначив t = 2x, запишем неравенство в виде р ≠ t3 – 2t2 + t. Так как t = 2x – непрерывная возрастающая функция на R, то при -1 ≤ x < 2 переменная
2-1 ≤ t <22 ↔
0,5 ≤ t < 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда р отлична от значений функции f(t) = t3 – 2t2 + t при 0,5 ≤ t < 4.
Найдём сначала множество значений функции f(t) на отрезке [0,5;4], где
она всюду имеет производную f’(t) =3t2 – 4t + 1.
Следовательно, f(t) дифференцируема, значит, и непрерывна на отрезке
[0,5;4]. Из уравнения f’(t) = 0 найдём критические точки функции t =
1/3, t = 1, первая из которых не принадлежит отрезку [0,5;4], а вторая
принадлежит ему. Так как f(0,5) = 1/8, f(1) = 0, f(4) = 36, то, по
свойству дифференцируемой функции, 0 – наименьшее, а 36 – наибольшее значение
функции f(t) на отрезке [0,5;4]. Тогда f(t), как непрерывная
функция, принимает на отрезке [0,5;4] все значения от 0 до 36 включительно,
причём значение 36 принимает только при t = 4, поэтому при 0,5 ≤ t < 4,
она принимает все значения из промежутка [0;36). Тем самым
![]()
Заключение.
Данная тема имеет практическое значение. В школьном курсе математики
изучается тема “Область значения функции”. Такие задачи обязательно содержатся в
заданиях различных математических тестов, в частности в заданиях единого
государственного экзамена.
Результаты работы можно использовать на уроках и дополнительных занятиях при
подготовке учащихся выпускным и вступительным экзаменам, при самостоятельной
подготовке учащихся по данной теме.
Литература.
- Сильвестров В.В. Множество значений функции: Учебное пособие.– Чебоксары, 2004.
- Амелькин В.В., Рабцевич В.Л. Задачи с параметрами.– Минск, 1996.
- Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. – Москва – Харьков, 1998.
- Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с параметрами: Учебное пособие. 4-е изд., доп., перераб. – М., 2006.
- Сильвестров В.В. Неравенства с параметром на едином государственном экзамене // Математика для школьников. 2008. № 2.