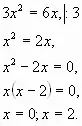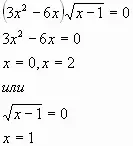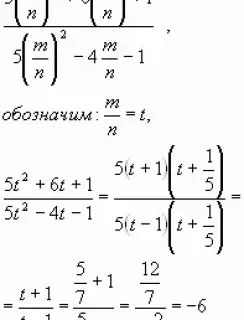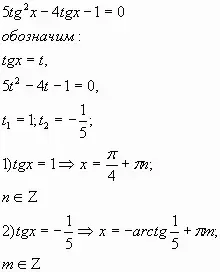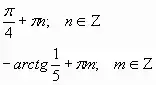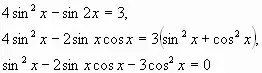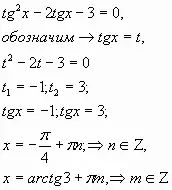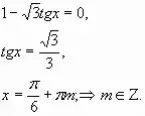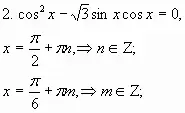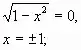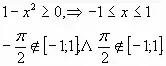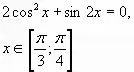«Открытый урок»
Коршунова Елена Робертовна

Урок алгебры по теме: "Однородные тригонометрические уравнения" с использованием технологии "Эвристическая беседа". 10-й класс

01.02.2006

Тип урока: “Урок изучения, первичного закрепления и применения новых знаний” ( I – II тип ).

Цели урока:

  1. Образовательные: актуализация знаний об уравнениях, закрепление знаний о равносильных уравнениях, понятий области определений и области значений; повторение тригонометрических уравнений, сводящихся к квадратным; знакомство с однородными тригонометрическими уравнениями и способами отбора корней уравнения; укрепление умений и навыков в работе по образцу и в сходных условиях; перенос знаний в новые условия.
  2. Развивающие: развитие логического мышления, познавательного интереса, творческой активности; развитие общеучебных навыков и умений – организационных, интеллектуальных и коммуникативных.
  3. Воспитательные: воспитание взаимопомощи, культуры общения, способствующей созданию благоприятного психологического климата, направленного на личностно-ориентированный подход к обучению и воспитанию.

Технология урока: Эвристическая беседа

Эвристика (от греческого heurisko – нахожу)

  • методика обучения, основанная на открытии или догадке;
  • система обучения путем наводящих вопросов;
  • метод обучения, способствующий находчивости, активности.

БЭС: “Восходящий к Сократу метод обучения (т.н. сократические беседы)”

“Лучшее, что может сделать Учитель для Учащегося, состоит в том, чтобы путем неназойливой помощи подсказать ему блестящую идею … Хорошие идеи имеют своим источником прошлый опыт и ранее приобретенные знания”. (Д. Пойя (математик и методист))

Этап:

 I

Содержание этапа:

 Организационный

Время выполнения:

 5 минут

ТДЗ (триединая дидактическая задача):

 Подготовка учащихся к работе на уроке, постановка цели, мотивация деятельности.

Примечания:

 Общеучебные умения и навыки:

Учебно-организационные:

  1. Умение планировать
  2. Умение контролировать

Учебно-интеллектуальные:

  1. Умение выделять главное и существенное

Учебно-коммуникативное:

  1. Знание основных понятий,
  2. Знание определений, понятий, их существенных признаков,

Умение проводить доказательства, рассуждать при выполнении аналитических заданий.

 

Содержание учебного материала

Деятельность учителя

Деятельность учащегося

Методы обучения

ФОПД
ОУУН
Приветствие, проверка готовности к уроку, пособий, раздаточного материала, доски и т.д.

Организация внимания, краткий рассказ о новой форме работы на уроке – эвристической беседе, постановка задач урока.

 Учитель рассказывает о сущности эвристического обучения, мотивирует учащихся на работу на уроке. Учащиеся включаются в активную работу на уроке. Словесный ФОПД: Общеклассная

 

Этап:

 II

Содержание этапа:

 Проверка ДЗ, подготовка учащихся к усвоению новых знаний

Время выполнения:

 15 минут

ТДЗ (триединая дидактическая задача):

Выявление уровня теоретических знаний, актуализация знаний о равносильности уравнений, области определения и области значений;

Развитие математической речи, логического мышления;

Воспитание внимания, контроля, умение выделять главное и существенное.

Примечания:

  

 

Содержание учебного процесса

Деятельность учителя

Деятельность учащегося

Методы обучения

ФОПД
ОУУН
1. Анализ домашнего задания

1. Решение уравнения:

    a)

    б)

    в)

Вопрос (В.)

Почему обе части уравнения можно разделить на 3 и нельзя на х?

 

 

 

 

Можно ли разделить обе части уравнения на ?

 Ответ (О.)

При делении на х происходит потеря корня х=0

 

 

 

 

Да, т.к. при любых значениях х

 Репродуктивный, вопросно-ответный

 

 

 

 

 

 

 

 ОПД:

Общеклассная + индивидуальная

 

 

 

 

 

 

 
2. Найдите ошибку:

    а)

    б)

    Ответ: 1; 2.

3. Итог

1. Что значит решить уравнение?

2. Какие уравнения называются равносильными?

3. Область определения (уравнения 2. а) б))

4. Область значений? (Почему уравнения:

не имеют решений?)

4. Централизованное тестирование

    Сократить дробь:

     

    Вычислить ее значение при:

Сформулируйте условия равенства произведения нулю

 

 

 

Сформулируйте условия равенства дроби нулю. Выделите главное и существенное

 

 

 

Опрос теоретического материала

 

 

Найти область определения функции

 

 

 

 

Каким приемом пользовались?

 

 

 

Что побудило воспользоваться этим приемом?

 

 

 

 

А.П. Чехов (мотивация учащихся на последующую работу на уроке)

 х=0 не является корнем уравнения

 

 

 

х=1 не является корнем уравнения

 

 

 

 

 

 

 

 

 

 

 

 

 

Числитель и знаменатель разделим на

 

Не знаем m и n, но знаем из условия.

 Поисковый

 

 

 

 

 

 

 

 

 

 

 

 

 

Вопросно-ответный

 

 

 

 

 

Индуктивный, наглядный (фрагменты на доске)

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

ФОПД: Общеклассная

 

 

 

 

Индивидуальный (учащийся готовит ответ заранее)

 

Этап:

 III

Содержание этапа:

 Изучение нового материала

Время выполнения:

 15 минут

ТДЗ (триединая дидактическая задача):

 Восприятие учащимися и первичное осознание нового учебного материала, осмысление связей и отношений в объектах изучения;

Развитие логического мышления, умение работать в проблемной ситуации;

Воспитание умения слушать и беседовать, выдвигать гипотезы, конспектировать.

Примечания:

  

 

Содержание учебного материала

Деятельность учителя

Деятельность учащегося

Методыобучения

ФОПД
ОУУН
1. Постановка проблемной ситуации

1. При изучении тригонометрических уравнений, сводящихся к квадратным:

а)

б)

в)

использовали метод введения новой переменной, предварительно преобразовав данное уравнение к уравнению относительно одной тригонометрической функции.

  

Какие формулы тригонометрии использовали?

  

 

  

Репродуктивный

  

ФОПД: Общеклассная + индивидуальная
ОУУН: I гр. 1)
2. Рассмотрим уравнение:

Данное уравнение нельзя свести к уравнению относительно функций sinx или cosx

 В чем проблема в решении этого уравнения? Уравнение содержит одновременно sinx и cosx Поисковый ФОПД: Общеклассная
Разделим обе части уравнения на

Получим:

Значения переменной х, при которых cosx=0, не являются решениями этого уравнения,, так как, если cosx=0, то должно выполняться равенство , а косинус и синус не могут быть одновременно равными нулю. Поэтому можно обе части уравнения разделить на и при этом получить уравнение, равносильное данному.

Ответ:

Итак, мы научились решать однородное уравнение 2-й степени

3. Изменим ситуацию

 Попробуем свести это уравнение к уравнению относительно tgx

 

 

 

 

 

 

 

Деление на выражения, содержащие переменную, обычно приводит к потере корней уравнения.

Вопрос: Почему в данной ситуации получаем уравнение, равносильное данному?

 Воспользуемся приемом, который мы применияли в задании: Сократить дробь

( деление на )

 

 

 

 

 

Учащиеся доказывают, что sinx и cosx не могут быть одновременно равны нулю

а) Указав формулы

б) Показав на тригонометрической окружности

в) Приведя к противоречию с основным тригонометрическим тождеством.

  

 

 

 

 

 

 

 

 

Словесный

  

 

 

 

 

 

 

 

 

ФОПД:
Общеклассный
ОУУН: III гр.

 

Этап:

 IV

Содержание этапа:

 Первичное закрепление знаний;

Первичная проверка усвоения знаний.

Время выполнения:

 10 минут

ТДЗ (триединая дидактическая задача):

 Проверка осознанности усвоения учащимися нового материала;

Коррекция знаний;

Пробное применение знаний в конкретных условиях.

Примечания:

  

 

Содержание учебного материала

Деятельность учителя

Деятельность учащегося

Методыобучения

ФОПД
ОУУН
Письменная работа учащихся по книге “Мониторинг качества образования” под редакцией Т.К. Чекмаревой: “Диагностирующие задания для проверки усвоения общеучебных умений и навыков по алгебре и началам анализа, 10 класс” Учитель заранее раздает распечатанные материалы для самостоятельной работы учащихся и осуществляет выборочный контроль Учащиеся выполняют самостоятельную работу по первичной проверке усвоения знаний Практический (самостоятельная работа) ФОПД:
Индивидуальный
ОУУН:
I гр. 1), 2)
II гр.

Этап:

 V

Содержание этапа:

 Применение знаний, умений и навыков в новых условиях

Время выполнения:

 35 минут

ТДЗ (триединая дидактическая задача):

 Проверка полноты и осознанности усвоения знаний, их актуализация, усвоение образца комплексного применения знаний в измененных условиях;

Развитие логического мышления, умений анализировать, выделять главное и существенное;

Воспитание грамотной математической речи.

Примечания:

  

 

Содержание учебного процесса

Деятельность учителя

Деятельность учащегося

Методыобучения

ФОПД
ОУУН
Решить уравнения:

1.

Разделим на :

 Вопрос:

Является ли данное уравнение однородным?

Можно ли сделать его однородным?

 

 

 

 

 

-“-“-“-“-“-“

Вопрос:

Как найти корни данного уравнения?

 Ответ:

Используем основное тригономнтрическое тождество:

 

 

 

 

 

-“-“-“-“-“-“

Ответ:

По теореме, обратной теореме Виета

 Поисковый, индуктивный ОУУН: III гр.

 

 

 

 

 

 

 

 

ОУУН: III гр.
2.

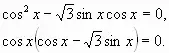
Условия равенства нулю произведения двух множителей:

Или:

Разделим обе части уравнения на cosx:

Ответ:

Вопрос:

Является ли данное уравнение однородным?

Почему нельзя разделить обе части уравнения на ?

Как решить уравнение?

 

Какое уравнение в скобках?

Можно ли обе части уравнения разделить на sinx?

 

 Ответ:

Ур-е однородное (неполное). При делении на произойдет потеря корней вида:

Вынести cosx как общий множитель за скобку.

Это однородное ур-е 1-й степени.

Да, получим уравнение относительно ctgx/

   ФОПД:
Общеклассное
ОУУН: III гр.

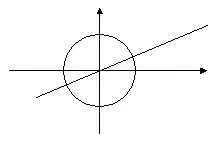
4. Решение уравнений с выборкой решений (отбор корней уравнений)

1. Рассмотрим уравнение:

,

и выберем корни, принадлежащие промежутку: .

Из (1): а)

I группа б)

Из (2) а)

Три корня:

II группа

Тригонометрическая окружность

Нули функции y=cosx

  

Вопрос:

Когда мы выполняем отбор корней уравнений?

 

 

Какими способами можно осуществить отбор корней?

  

Ответ:

Должен быть указан конкретный промежуток принадлежности корней

1) Перебор целых значений

2) Тригонометрическ. Окружность

3) Графики тригонометрических функций

  

 

_________, вопросно-ответный, наглядный (чертежи на доске)

 ФОПД: Групповой
ОУУН: III гр.
Рассмотрим уравнение:

Условие равенства нулю произведения трех множителей:

  1. sinx – 2 = 0, sinx = 2

Уравнение не имеет решений, так как

!!!

3.

Но !

Следовательно,

Ответ:

Вопрос:

Промежуток принадлежности корней не указан. Надо ли проводить отбор корней?

Выделите главное и существенное при решении уравнения.

Главное:

Условие равенства нулю.

Существенное:

Проверка корней

 Ответ:

Да, т.к. произведение множителей равно нулю, если один из множителей равен нулю, а другие при этом не теряют смысла.

 Проблемно-поисковый ФОПД: Общеклассное
ОУУН: III гр.

 

 

 

 

 

ОУУН: II гр.

  

Этап:

 VI

Содержание этапа:

 Информация о домашнем задании

Время выполнения:

 3 минуты

ТДЗ (триединая дидактическая задача):

 Закрепление СУН и самоконтроль

Примечания:

  

 

Содержание учебного процесса

Деятельность учителя

Деятельность учащегося

Методы обучения

ФОПД
ОУУН
Учебник А.Н. Колмогорова “Алгебра и начала анализа 10-11 классы”

№ 169(а, в),   № 170(г),  № 171(а).

Дополнительное задание:

Решить уравнение:

1)

2)

3)

(резерв)

4)

(РЭА им. Плеханова)

 Учитель дает дифференцированное домашнее задание Учащиеся выбирают задание, соответствующее их уровню обученности Словесный ФОПД:
Общеклассный + индивидуальный

 

Этап:

 VII

Содержание этапа:

 Подведение итогов урока, рефлексия

Время выполнения:

 5 минут

ТДЗ (триединая дидактическая задача):

 Обобщение знаний, полученных на уроке,

анализ овладения способами деятельности

Примечания:

  

 

Содержание учебного материала

Деятельность учителя

Деятельность учащегося

Методы обучения

ФОПД
ОУУН
Повторили вопросы, связанные с решением уравнений: равносильность, область определения, область значений;

Научились решать однородные тригонометрические уравнения;

Отбор корней уравнения.

 Учитель дает установку на рефлексию Учащийся осуществляет рефлексию Аналитико-синтетический ФОПД:
Общеклассный
aid: 311638