Результаты:

• Владеть основными теоретическими понятиями темы.
• Уметь вычислять площади криволинейных фигур при помощи интеграла.

ХОД ЗАНЯТИЯ

I. Организационный момент

1) Предварительное определение уровня знаний - 6 мин.

2) Мотивация - 2 мин.

(Задание 8)

Организация самостоятельной работы студентов по основным вопросам занятия - 23 мин.

(Учебный материал 8, задание 8.1 - Приложение)

• Деятельность преподавателя: Организует работу студентов по основным вопросам темы занятия.
• Деятельность студентов: Самостоятельно работают по основным вопросам темы занятия:
  • определение криволинейной трапеции;
  • формула Ньютона-Лейбница;
  • примеры вычисления площадей криволинейной трапеции при помощи интеграла.

II. Подведение итогов занятия.

1) Проверка степени усвоения материала - 12 мин.

(Задание 8.2)

2) Заполнение дневников - 2 мин.

Задание 8

III. Предварительное определение уровня знаний

Ф.И. (выполняющего)______________________________
Ф.И. (проверяющего) ______________________________

Задание 1. Вспомните формулы первообразных и правила вычисления первообразных, составив таблицу:

Функция f (x)	Общий вид первообразных для f (x)
f (x) = k (постоянная)	F (X) =
f (x) = xn, n =/= -1	F (X) =
f (x) = cosx	F (X) =
f (x) = sinx	F (X) =
f (x) =	F (X) =
f (x) =	F (X) =
f (x) =	F (X) =
f (x) + g(x)
k * f (x)
f (kx + b)

Задание 2. Найдите общий вид первообразной для функции f (x) = sin x - 10х⁴ + 3, график которой проходит через точку М (0; 5).

Задание 8.1

IV. Закрепляющий материал

Задание 1. Ответьте устно на вопросы:

а) Какая фигура называется криволинейной трапеции?
б) Какими свойствами она обладает?
в) По какой формуле вычисляется площадь криволинейной трапеции?
г) Как вычислить площадь фигуры, ограниченной линиями:

• у = х² + 1 и y = 2х + 4 (слайд 9);
• у = х² и y = х² - 9х + 18,25 (слайд 10)?

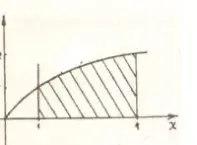
д) Как найти площадь изображенной на рис. 10 фигуры?

Рис.10

Задания 2-3. Найти площадь фигуры, ограниченной указанными линиями:

1) у = 3x² - 1, x = 1, x = 2 и осью ОХ;
2) у = cos х, у = 1/2, х = 0 и х = /3.
(продемонстрировать на интерактивной доске).

Задания 4-6. Попытайтесь, используя таблицу первообразных и формулу вычисления площади криволинейной трапеций, найти площадь фигуры, ограниченной указанными линиями:

1) у = 12х - 3x² и y = 0;
2) у = sin х, у = 2, х = 0 и х = ;
3) у = x², y = .
(по одному примеру студенты решают у интерактивной доски).

Задание 8.2

Лист 1

Проверка степени усвоения материала

Задание 1. Установите соответствие между функциями и их графиками (соедините стрелками):

	Функции	Криволинейные трапеции
1	у = - (x - 1)3 , y > 0, x = 0
2	у = - 3х - x2 , y = 0
3	у = sin x , y = 0, x = , x =
4	у = , y = 0, x = 1, х = 4

Лист 2

Задание 2. Ответьте на вопросы:

а) Дайте определение криволинейной трапеции?
б) Как читается запись S = F(b) - F(a)?
в) Запишите формулу Ньютона-Лейбница.
г) Объясните, как найти площадь фигур, изображенных на рис. 11, 12:

Рис. 11

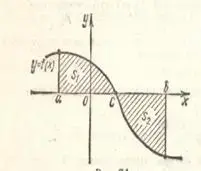
Рис. 12

Задание 3. Программированный контроль

Задания		Ответы
Вычислить площадь фигуры, ограниченной линиями:
I вариант	II вариант	1	2	3	4
у = 0,5x2 , y = 0, x = 1, х = 2	у = - 6х, у = 0, х = 4	32	7/6	48	11/6
у = , у0, x = 1, x = 4	у = - х2 + 4 и y = 0	7/3	32/3	14/3	16/3

Дополнительное задание. Вычислить площадь фигуры, ограниченной указанными линиями: y = 0,5x + 2, у = - x + 5 и у = 0.

Домашнее задание: учебник А.Н. Колмогорова Алгебра и начала анализа 10-11

• стр. 185 - 187 читать, выучить определение, теорему (без доказательства);
• стр. 188 № 353 (а, в), № 354 (б,г)

Эталон

Проверка степени усвоения материала

Задание 1. 1 - 3, 2 - 2, 3 - 4, 4 - 1

Задание 2.

а) Пусть на отрезке [a; b] оси ОХ задана непрерывная функция f (х), не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [a; b] и прямыми x = a и x = b называют криволинейной трапецией.

б) Площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [а; b].

в) F(b) - F(a)

г) Площадь фигуры, изображенной на рис. 8 находим как разность площадей S₁ и S₂, где S₁ - площадь фигуры, ограниченной прямыми у = 2х, у = 0, х = 2, а S₂ - площадь фигуры, ограниченной параболой у = х², прямыми у = 0, х = 2 (случай 4).
Площадь фигуры, изображенной на рис. 9 находим как сумму площадей S₁ и S₂ (случай 3).

Задание 3. Программированный контроль

Верные ответы:

• I вариант: 2, 3
• II вариант: 3, 2

Доп. задание: 13,5 (кв.ед.)

Оценочный лист

Ф.И. __________________________________________

Выделить в таблице ту позицию, которая вернее отражает ваше ощущение прошедшего занятия и вашего участия в нем