«Открытый урок»
Федорова Зоя Ивановна
20.03.2010

Урок математики по теме "Теорема о трех перпендикулярах"

Курсы университета «Первое сентября»

Цели урока:

Образовательная: доказать теорему о трех перпендикулярах, научить применять ее при решении задач.
Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.
Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы: компьютер, экран, проектор, проектная работа "Перпендикулярность прямых и плоскостей"

1. Фронтальный опрос.

а) Дайте определение перпендикуляра, основания перпендикуляра,расстояния от точки до плоскости, наклонной, основания наклонной, проекции наклонной.
б) Сформулируйте признак перпендикулярности прямой и плоскости.
в) Сформулируйте теорему, обратную теореме о свойстве медианы в равнобедренном треугольнике.
г) Задачи:

1) АА1 - перпендикуляр к плоскости LANG="E">?, АВ - наклонная. Найти х.
2) Прямая а перпендикулярна плоскости АВС, угол АСВ равен 90о, АС = 4, МD=3. Найти МС. (МС=1)

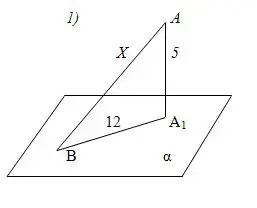
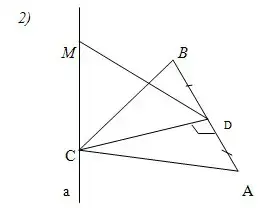
Рисунок 1

2. Изучение нового материала.

Новый материал учитель объясняет с помощью презентации "Теорема о трех перпендикулярах".

3. Закрепление изученного материала.

1) Задача № 45 решается с помощью презентации.

Или. Рассмотрим треугольники AOS , BOS, COS . Они равны по двум катетам. Следовательно, AS=BS= CS

2) Задача 2. Прямая а перпендикулярна плоскости АВС. MD = 13. АС = 15, ВС = 20.

АС ВС, МD АВ. Найти MC.

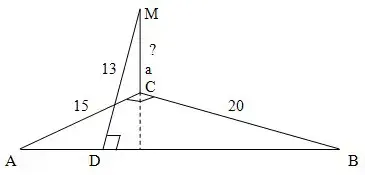
Рисунок 2

Решение:

  1. Из треугольника АВС найдем гипотенузу АВ. АВ=25;
  2. Соединим точки С и D. По теореме о трех перпендикулярах CD перпендикулярно AB;
  3. Следовательно, AB : AC = AC : AD. Отсюда AВ = 9;
  4. Из треугольника ADC найдем катет DC = 12;
  5. Из треугольника MDC по теореме Пифагора найдем МС;
  6. MC = 5.

Задание на дом: п. 19, № 48.

Итог урока.

Приложение.

Приложения

Похожие уроки