Изучение многих физических и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые ВУЗы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса алгебры рассматривается только на немногочисленных факультативных или предметных курсах.
На мой взгляд, функционально-графический метод является удобным и быстрым способом решения уравнений с параметром.
Как известно, в отношении уравнений с параметрами встречаются две постановки задачи.

1. Решить уравнение (для каждого значения параметра найти все решения уравнения).
2. Найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.

В данной работе  рассматривается  и исследуется задача второго типа применительно к корням  квадратного трехчлена, нахождение которых сводится к решению квадратного уравнения.
Автор надеется, что данная работа поможет  учителям  при разработке уроков и при подготовке учащихся к ЕГЭ.

1. Что такое параметр

Выражение вида aх² + bх + cв школьном курсе алгебры называют квадратным трехчленом относительно х, где a, b, c – заданные действительные числа, причем, a =/= 0. Значения переменной х, при которых выражение обращается в нуль, называют корнями квадратного трехчлена. Для нахождения корней квадратного трехчлена, необходимо решить квадратное уравнение aх² + bх + c = 0.
Вспомним из школьного курса алгебры основные уравнения aх + b = 0;
aх2 + bх + c = 0. При поиске их корней, значения переменных a, b, c, входящих в уравнение считаются фиксированными и заданными. Сами переменные называют параметром. Поскольку, в школьных учебниках нет определения параметра, я предлагаю взять за основу следующий его простейший вариант.

Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

2. Основные типы и методы решения задач с параметрами

Среди задач с параметрами можно выделить следующие основные типы задач.

1. Уравнения, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству. Например. Решить уравнения: aх = 1, (a – 2)х = a² – 4.
2. Уравнения, для которых требуется определить количество решений в зависимости от значения параметра (параметров). Например. При каких значениях параметра aуравнение 4х² – 4 aх + 1 = 0 имеет единственный корень?
3. Уравнения, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Например, найти значения параметра, при которых корни уравнения (a – 2)х² – 2aх  + a + 3 = 0 положительные.
Основные способы решения задач с параметром: аналитический и графический.

Аналитический – это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Рассмотрим пример такой задачи.

Задача № 1

При каких значениях параметра а уравнение х² – 2aх + a² – 1 = 0 имеет два различных корня, принадлежащих промежутку (1; 5)?

Решение

х² – 2aх + a² – 1 = 0.
По условию задачи уравнение должно иметь два различных корня, а это возможно лишь при условии: Д > 0.
Имеем: Д = 4a² – 2(а² – 1) = 4.  Как видим дискриминант не зависит от а, следовательно, уравнение имеет два различных корня при любых значениях параметра а. Найдем корни уравнения: х₁ = а + 1, х₂ = а – 1
Корни уравнения должны принадлежать промежутку (1; 5), т.е.
Итак, при 2 < а < 4 данное уравнение имеет два различных корня, принадлежащих промежутку (1; 5) 

Ответ: 2 < а < 4.
Такой подход к решению задач рассматриваемого типа возможен и рационален в тех случаях, когда дискриминант квадратного уравнения «хороший», т.е. является точным квадратом какого либо числа или выражения или корни уравнения можно найти по теореме обратной т.Виета. Тогда, и корни не представляют собой иррациональных выражений. В противном случае решения задач такого типа сопряжено с достаточно сложными процедурами с технической точки зрения. Да и решение иррациональных неравенств требует от ученика новых знаний.

Графический – это способ, при котором используют графики в координатной плоскости (х;у) или (х;а). Наглядность и красота такого способа решения помогает найти быстрый путь решения задачи. Решим задачу № 1 графическим способом.
Как известно из курса алгебры корни квадратного уравнения (квадратного трехчлена) являются нулями соответствующей квадратичной функции: У = х² – 2ах + а² – 1. Графиком функции является парабола, ветви направлены вверх (первый коэффициент равен 1). Геометрическая модель, отвечающая всем требованиям задачи, выглядит так.

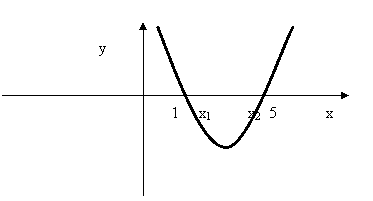
Теперь осталось «зафиксировать» параболу в нужном положении необходимыми условиями.

1. Так как парабола имеет две точки пересечения с осью х, то Д > 0.
2. Вершина параболы находится между вертикальными прямыми х = 1 и х = 5, следовательно абсцисса вершины параболы х_о принадлежит промежутку (1; 5), т.е.
   1  <х_о < 5.
3. Замечаем, что у(1) > 0, у(5) > 0.

Итак, переходя от геометрической модели задачи к аналитической, получаем систему неравенств.

Ответ: 2 < а < 4.

Как видно из примера, графический способ решения задач рассматриваемого типа возможен в случае, когда корни «нехорошие», т.е. содержат параметр под знаком радикала (в этом случае дискриминант уравнения не является полным квадратом).
Во втором способе решения мы работали с коэффициентами уравнения и областью значения функции  у = х² – 2ах + а² – 1.
Такой способ решения нельзя назвать только графическим, т.к. здесь приходится решать систему неравенств. Скорее этот способ комбинированный: функционально-графический. Из этих двух способов последний является не только изящным, но и наиболее важным, так как в нем просматриваются взаимосвязь между всеми типами математической модели: словесное описание задачи, геометрическая модель – график квадратного трехчлена, аналитическая модель – описание геометрической модели системой неравенств.
Итак, мы рассмотрели задачу, в которой корни квадратного трехчлена удовлетворяют заданным условиям в области определения при искомых значениях параметра.

А каким еще возможным условиям могут удовлетворять корни квадратного трехчлена при искомых значениях параметра?

На этот вопрос  автор  ответит в данной работе. В данной работе показан  алгоритм решения задач и обобщен полученный опыт.

Примеры решения задач