Использование компьютерных программ на уроках математики
Цели урока:
- Закрепить теоретический материал по теме "Прямоугольник. Ромб. Квадрат".
- Совершенствовать навыки решения задач по теме.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
Теоретическая самостоятельная работа
Заполнить таблицу, отметив знаки + (да), - (нет).
| Параллелограмм | Прямоугольник | Ромб | Квадрат | |
| 1. Противолежащие стороны параллельны и равны. | ||||
| 2. Все стороны равны. | ||||
| 3. Противолежащие углы равны, сумма соседних углов равна 1800. | ||||
| 4. Все углы прямые. | ||||
| 5. Диагонали пересекаются и точкой пересечения делятся пополам. | ||||
| 6. Диагонали равны. | ||||
| 7. Диагонали взаимно перпендикулярны и являются биссектрисами его углов. |
Правильные ответы:
| параллелограмм | прямоугольник | ромб | квадрат | |
| 1. | + | + | + | + |
| 2. | - | - | + | + |
| 3. | + | + | + | + |
| 4. | - | + | - | + |
| 5. | + | + | + | + |
| 6. | - | + | - | + |
| 7. | - | - | + | + |
Проверочный тест
Вариант 1.
1. Любой прямоугольник является:
а) ромбом; б) квадратом; в) параллелограммом; г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник - …
а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.
3. Ромб - это четырехугольник, в котором …
а) диагонали точкой пересечения делятся пополам и равны;
б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;
в) противолежащие углы равны, а противолежащие стороны параллельны;
г) нет правильного ответа.
Вариант 2.
1. Любой ромб является:
а) квадратом; б) прямоугольником; в) параллелограммом; г) нет правильного ответа.
2. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм - …
а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.
3. Прямоугольник - это четырехугольник, в котором …
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в) два угла прямые и две стороны равны;
г) нет правильного ответа.
Ответы к тесту:
1 вариант: 1 - в); 2 - г); 3 - б).
2 вариант: 1 - в); 2 - а); 3 - а).
Проверка домашнего задания
III. Решение задач
Решение задач на готовых чертежах (устно)
1) Рис.1. АВСD - ромб. Найти: МD + DN.
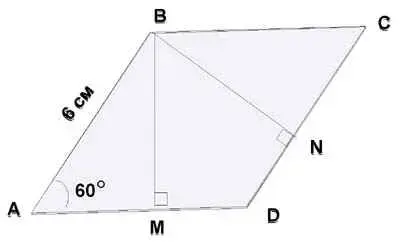
Рис.1.
2) Рис.2. АВСD - ромб. Найти: ![]() СВЕ.
СВЕ.
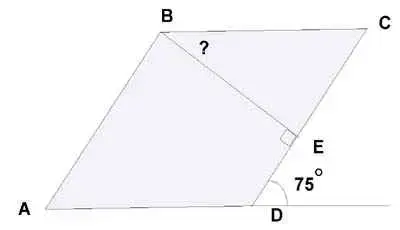
Рис.2.
Ответы к задачам на готовых чертежах:
1) МD + DN = 6 см.
2) ![]() СВЕ = 150.
СВЕ = 150.
Решение задач у доски с краткой записью
1) Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 300 меньше другого.
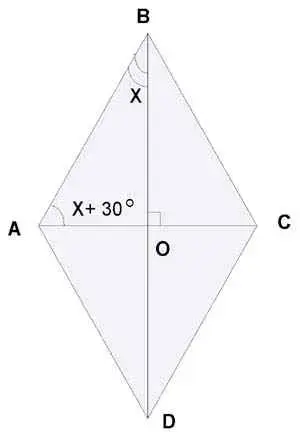
Рис.3.
Решение:
Диагонали ромба взаимно перпендикулярны, поэтому треугольник АОВ - прямоугольный (рис.3). Пусть в ?АОВ ![]() АВО = х, тогда
АВО = х, тогда ![]() ВАО = х + 300, значит
ВАО = х + 300, значит ![]() АВО +
АВО + ![]() ВАО = х + х + 300 = 900, и
х = 300.
ВАО = х + х + 300 = 900, и
х = 300.
![]() АВО = 300,
АВО = 300, ![]() ВАО = 600, а т.к. диагонали ромба являются биссектрисами его углов,
то
ВАО = 600, а т.к. диагонали ромба являются биссектрисами его углов,
то ![]() ВАD = 1200,
ВАD = 1200, ![]() АВС = 600.
АВС = 600.
Противолежащие углы в ромбе равны, тогда ![]() АDС =
АDС = ![]() АВС = 600,
АВС = 600, ![]() ВСD =
ВСD = ![]() BAD = 1200.
BAD = 1200.
Ответ: 600, 1200, 600, 1200. Рис.3.
2) Угол между диагоналями прямоугольника равен 800 . Найдите углы между диагональю прямоугольника и его сторонами.
Решение:
Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит ВО = ВD/2 = АС/2 =АО и ?АОВ - равнобедренный (рис.4.), тогда ![]() ОАВ =
ОАВ =
![]() ОВА = 500. В прямоугольнике все углы прямые, тогда
ОВА = 500. В прямоугольнике все углы прямые, тогда ![]() ОАD =
ОАD = ![]() ВАD -
ВАD - ![]() ОАВ = 900 - 500 = 400.
ОАВ = 900 - 500 = 400.
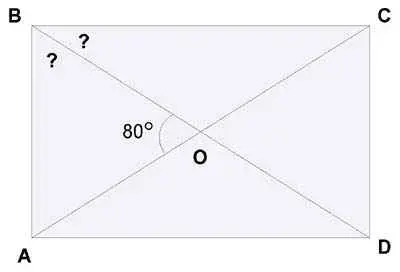
Рис.4.
Ответ: 500, 400.
3) В ромбе ABCD биссектриса угла ВAC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите угол АNВ, если ![]() АМС = 1200
.
АМС = 1200
.
Решение:
В ромбе (рис.5.) противолежащие углы равны и диагонали являются биссектрисами его углов, т.е. ![]() ВАС =
ВАС = ![]() ВАD : 2 =
ВАD : 2 =![]() ВСD : 2 =
ВСD : 2 = ![]() ВСА. Т.к. АМ - биссектриса
ВСА. Т.к. АМ - биссектриса ![]() ВАС, а
ВАС, а
![]() ВАС =
ВАС = ![]() ВСА, то
ВСА, то ![]() МАС =
МАС = ![]() МСА : 2.
МСА : 2.
В треугольнике АМС ![]() МАС +
МАС + ![]() МСА = 1800 -
МСА = 1800 - ![]() АМС =
1800 -1200 = 600.
АМС =
1800 -1200 = 600. ![]() МАС =
МАС = ![]() МСА : 2, тогда
МСА : 2, тогда ![]() МАС = 200,
МАС = 200, ![]() ВАС = 400.
ВАС = 400.
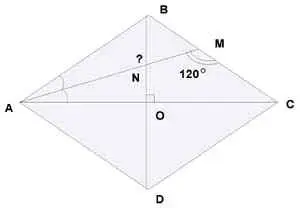
Рис.5.
В ромбе диагонали взаимно перпендикулярны, треугольник АОВ - прямоугольный, ![]() АВО = 900 -
АВО = 900 - ![]() ВАО
= 500. Рис.5.
ВАО
= 500. Рис.5.
В треугольнике АВN ![]() BAN =
BAN = ![]() МАС = 200,
МАС = 200, ![]() ABN =
500, тогда
ABN =
500, тогда
![]() ANB = 1800 - (200 + 500) = 1100.
ANB = 1800 - (200 + 500) = 1100.
Ответ: ![]() ANB = 1100.
ANB = 1100.
IV. Самостоятельная работа обучающего характера с последующей самопроверкой
1) В ромбе АВСD диагонали пересекаются в точке О, ![]() А = 310. Найдите углы треугольника ВОС.
А = 310. Найдите углы треугольника ВОС.
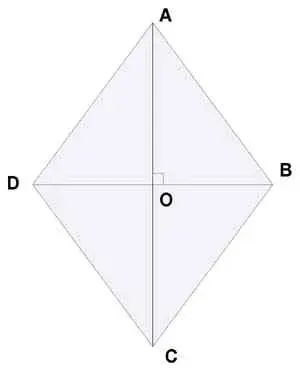
Рис.6.
Решение:
а) Рис.6. ![]() А =
А = ![]() С = 310; СО - биссектриса
С = 310; СО - биссектриса ![]() С,
С,
![]() ОСВ = 15030';
ОСВ = 15030';
б) Треугольник СОВ - прямоугольный, ![]() ВОС = 900,
ВОС = 900, ![]() ОСВ = 15030',
ОСВ = 15030',
![]() ОВС = 74030'.
ОВС = 74030'.
Ответ: 900, 15030', 74030'.
2) В прямоугольнике АВСD О - точка пересечения диагоналей, ВН и DЕ - высоты треугольников АВО и СОD соответственно, ![]() ВОН = 600 , АН = 5 см.
Найдите ОЕ.
ВОН = 600 , АН = 5 см.
Найдите ОЕ.
Решение:
а) Треугольник АВО - равнобедренный (рис.7.), ВО = ОА т.к. в прямоугольнике диагонали равны и точкой пересечения делятся пополам, а т.к. ![]() ВОА =
600, то ?АВО - равносторонний, поэтому высота ВН - медиана треугольника АВО, тогда ОН = 5 см.
ВОА =
600, то ?АВО - равносторонний, поэтому высота ВН - медиана треугольника АВО, тогда ОН = 5 см.
б) Треугольник ОВН = треугольнику ОDЕ ( по стороне и двум прилежащим углам ВО = ОD, ![]() ВОН =
ВОН = ![]() DОЕ -
вертикальные,
DОЕ -
вертикальные, ![]() ОВН =
ОВН = ![]() ОDЕ - накрест лежащие при параллельных ВН и DЕ и секущей ВD).
ОDЕ - накрест лежащие при параллельных ВН и DЕ и секущей ВD).
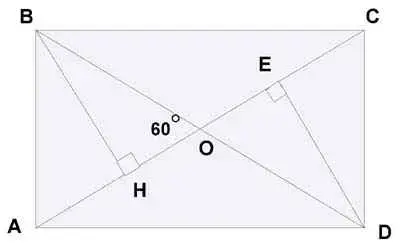
Рис.7.
Из равенства треугольников следует равенство сторон
ОН = ОЕ = 5 см.
Ответ: ОЕ = 5 см.
3) В ромбе АВСD угол В тупой. На стороне АD взята точка К, ВК![]() АD. Прямые ВК и АС пересекаются в точке О, АС = 2ВК. Найдите угол АОВ.
АD. Прямые ВК и АС пересекаются в точке О, АС = 2ВК. Найдите угол АОВ.
Решение:
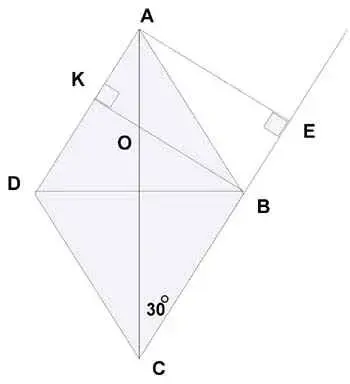
Рис.8.
а) Проведем АЕ ![]() АD (рис.8), тогда КВ = АЕ, АС = 2АЕ,
АD (рис.8), тогда КВ = АЕ, АС = 2АЕ, ![]() АСЕ = 300.
АСЕ = 300.
б) ![]() СОВ = 600,
СОВ = 600, ![]() АОВ = 1200.
АОВ = 1200.
Ответ: 1200.
V. Подведение итогов урока
Домашнее задание:
Докажите, что биссектрисы всех четырех углов прямоугольника (не являющегося квадратом) при пересечении образуют квадрат.